Относительный покой жидкости

Жидкость находится в относительном покое при её движении вместе с резервуаром как единое целое. Различают относительный покой жидкости в цилиндрическом сосуде, вращающемся вокруг вертикальной оси (центробежный фильтр грубой очистки – центрифуга), при движении резервуара горизонтально и прямолинейно с постоянным ускорением, при движении резервуара вертикально с постоянным ускорением.

Например, при движении автомашины, оснащённой резервуаром для перевозки жидкостей, при расчёте резервуара на прочность необходимо учитывать увеличение давления на стенки резервуара как при прямолинейном движении автомашины, так и при повороте.

Цилиндрический сосуд, равномерно вращающийся относительно вертикальной оси.Рассмотрим цилиндрический сосуд радиусом R, вращающийся с постоянной угловой скоростью ω (рис. 2.11, а). Через некоторое время жидкость под действием сил трения будет вращаться с той же скоростью, что и сосуд.

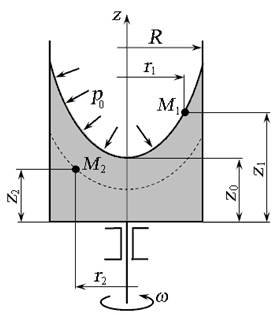
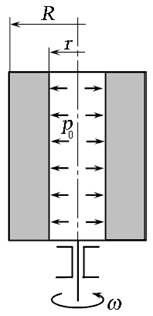
а) б)

Рис. 2.11. Относительный покой жидкости во вращающемся сосуде

На любую частицу жидкости с массой ∆m во вращающемся с постоянной угловой скоростью ω сосуде действуют:

- сила тяжести G = ∆mg;

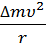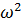- центробежная сила F_ц = = ∆m r.

В данном случае давление в любой точке покоящейся жидкости определяется двумя координатами - по вертикали высота z, по горизонтали радиус r. Поверхностью равного давления будет являться поверхность параболоида вращения, уравнение поверхности которого:

,

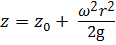где z – координата любой точки, лежащей на поверхности параболоида (на поверхности равного давления), например, z₁;

z₀ – координата вершины параболоида.

Давление в любой точке рассматриваемой жидкости:

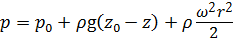. (2.11)

Повышение давления в жидкости, возникающее вследствие её вращения:

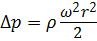. (2.12)

В случае, когда сила тяжести пренебрежительно мала в сравнении с центробежной силой ( 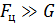), поверхностями равного давления будут поверхности, параллельные боковым стенкам сосуда (рис. 11, б). Давление, оказываемое на боковые стенки сосуда:

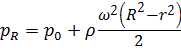. (2.13)

Прямолинейное движение резервуара с постоянной скоростью.

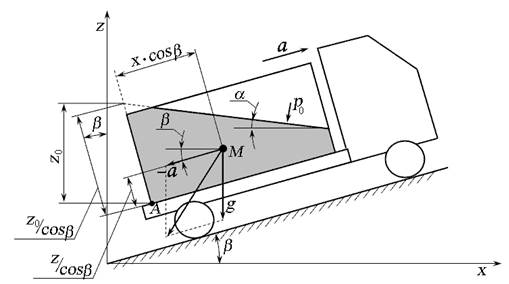
Рис. 2.12. Прямолинейное движение резервуара

Рассмотрим прямолинейное движение резервуара с жидкостью по наклонной поверхности (рис. 2.12), особенностями которого являются:

- поверхностью уровня является множество плоскостей, параллельных свободной поверхности жидкости;

- любая из поверхностей уровня наклонена к поверхности горизонта под углом α;

- сумма единичных сил в проекции на ось z равна 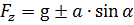(«–» при движении вверх по наклонной поверхности, «+» при движении вниз);

- сумма единичных сил в проекции на ось х равна .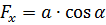

Давление в любой точке покоящейся жидкости (например, в т. М):

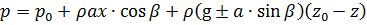. (2.14)

Из уравнения (2.14) видно, что максимальное давление будет в точке с координатами x = 0, z = 0 (точка А) при β = max. При движении по горизонтальной поверхности (β = 0):

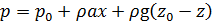. (2.15)