Общие принципы калориметрических измерений.

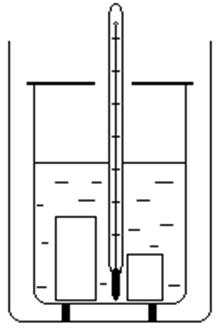Рис.3.

Устройство калориметра (рис.3) таково (наличие двух цилиндрических стаканов, разделенных воздушным промежутком, обладающим малой теплопроводностью), что теплообмен с окружающей средой у внутреннего сосуда незначителен. Если во внутреннем сосуде находится некоторая совокупность тел, не находящихся в состоянии теплового равновесия, то до его установления будет происходить передача внутренней энергии между частями, составляющими систему, от одних тел к другим (теплообмен). С течением времени система тел придет в равновесное состояние, т.е. все части системы будут иметь одинаковую температуру (нулевое начало термодинамики). Перераспределение внутренней энергии (количества теплоты) при этом удовлетворяет первому началу термодинамики и калориметрическому уравнению:

Q_{_получ} = Q_отд (9)

где:

- Q_{_получ} – количество теплоты, полученное телами, входящими в систему, у которых внутренняя энергия увеличилась; наблюдаются фазовые переходы или повышение температуры.

- Q_отд – количество теплоты, отданное телами, входящими в систему, у которых внутренняя энергия уменьшилась: охлаждение, кристаллизация.

Если нет процессов, протекающих на микроуровне, то нет и понятия о количестве теплоты. Количество теплоты характеризует элементарный или конечный процесс теплообмена: dQ или Q соответственно.

§5. Определение удельной теплоты плавления льда при атмосферном давлении (определяется по барометру и пересчитывается в Па с учетом 3^х значащих цифр).

Пусть в калориметре массы m_к находится вода массы m_в при t_о и лед массы m_л при t_пл.(t_пл при p = 760 мм. рт. ст. равна 0 °C). Тогда в системе (вода, внутренний сосуд калориметра, лед, термометр) происходит тепловой процесс, в результате которого лед плавится и устанавливается для всех тел системы общая температура t_к.

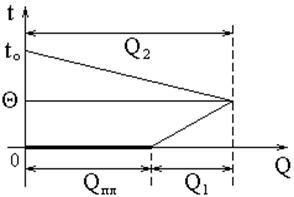Графически (в координатах t, Q) процесс, протекающий в калориметре, изображен на рис. 4. Пренебрегая теплообменом с окружающей средой, имеем:

Q_пл + Q₁ = Q₂ (10)

Q_пл – теплота плавления льда;

Q₁ – количество теплоты, пошедшей на нагревание воды, полученной из льда;

Рис. 4.

Q₂ –количество теплоты, отданное остывающей воде, калориметру с мешалкой и термометром.

lm_л + c_вm_л(Q – 0º) = с_вm_в(t_o - Q) + с_кm_к(t_o - Q) + w(t_o - Q) (11)

Откуда

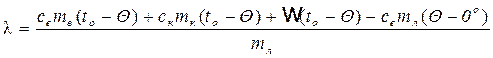(12)

Таким образом, для определения l данным методом необходимо знать:

m_л – массу льда (расплавившегося),

m_в – массу воды в калориметре (первоначально),

m_к – массу калориметра (внутреннего сосуда) с мешалкой,

t_о – начальная температура воды, калориметра и термометра (к моменту загрузки льда),

Q – установившаяся температура,

c_в, с_к, – удельные теплоемкости воды и калориметра (алюминиевого) -табличные значения,

w – теплоемкость термометра (его водяной эквивалент). В данной работе этой величиной можно пренебречь, т.е. w » 0.

Замечание 1.

Предположение о том, что W » 0 легко проверяется. Достаточно до проведения экспериментов со льдом в калориметр опустить такой же второй термометр, имеющий заметно меньшую температуру, и если показания основного термометра не изменяются, то, действительно, в нашем опыте теплоемкость его можно считать равной нулю.

К определению величин, входящих в (12) и сводится практическая задача по определению удельной теплоты плавления l льда данным методом.

Замечание 2.

*! Это замечание важно с двух точек зрения:

1) Сколько налить в калориметр воды и сколько добавить туда льда?

Важно знать, что удельная теплота плавления льда численно почти в 80 раз превышает удельную теплоемкость остывающей воды (числа сравниваются в одной системе единиц). А это значит, что для того, чтоб расплавить 1 г льда, вода массой 1 г должна остыть почти на 80^оС (точнее 79^оС). Теперь ясно, что воды следует взять чуть больше, чем половину внутреннего сосуда калориметра при температуре близкой к (50¸60)^оС (если позволяет термометр). Лед надо добавлять сухой (без влаги). Желательно, чтоб конечная температура воды в калориметре стала примерно на 10^оС ниже комнатной, - это уменьшит фактор теплообмена.

2) О сухом льде! Если лед будет содержать жидкость, то результат эксперимента будет существенно занижен. Промокайте-просушивайте лед хорошо! Не доводите его до фазы активного плавления. Пусть его температура будет даже на (0,2¸0,3)%. Самостоятельно сделайте эту оценку.

Приборы и материалы:

1. Калориметр. 2. Вода. 3. Термометр. 4. Лед.

5. Фильтровальная бумага. 6. Весы. 7. Электрическая плитка или кипятильник с нагреваемой водой.

Замечания:

1. Обратите внимание:

а) при взвешивании пустой калориметр должен быть сухим;

б) при опускании льда в воду лед должен быть сухим (просушите фильтровальной бумагой и сразу же опустите). Количество льда, которое необходимо опустить в калориметр, определяется с учетом ранее оговоренных условий, (это может быть несколько кусочков).

3. Масса расплавленного льда определяется как разность масс калориметра с водой после опыта и калориметра с водой до опыта.

4. Удельные теплоемкости воды, внутреннего сосуда калориметра и мешалки в данном опыте не определяются, (числовые данные приведены: проверьте, сравнив со справочными).

5. Во время опыта термометр из калориметра вынимать не рекомендуется, т.к. при этом можно вынести и капли жидкости, что ведет к занижению m_л и завышению l.

6. Окончательная (установившаяся) температура определяется как самое наименьшее показание термометра во время опыта (почему?) .

7. Первоначальное количество воды в калориметре должно быть, возможно, большим (почему?).

Таблица 1. c_в= 4,18·10³ 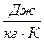; с_к= 0,896·10³ .

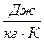mк, г	(mк+ mв), г	mв, г	(mк+mв+mл), г	mл, г	Dm (весов), г	tо, °С	Q, °С	Dtо, DQ, °С	eк = Dm/mк	eв = 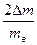,	eл =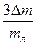

Расчеты.

Рекомендуем вначале сосчитать относительные приборные погрешности определения масс:

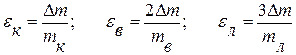
Есть основания полагать, что при взвешивании на электронных весах e_к и e_в малы (высокая степень точности). Погрешность на лед Dm_л=3Dm учитывается дважды и, видимо, ее придется учесть. В этом случае желательно вначале провести расчет l_расч. По формуле (12) без учета водяного эквивалента термометра, затем найти e по (13) и, наконец, Dl.

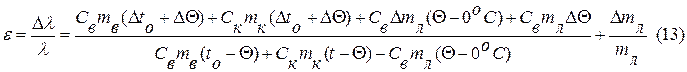
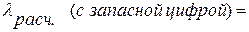
e =

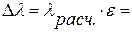
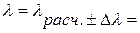
Расчеты и выводы:

Контрольные вопросы:

1. Сформулируйте начала термодинамики, используемые в проведенном эксперименте. В каком варианте они применимы?

2. Какие виды систематических погрешностей имеют место в предложенном методе определения l_пл льда? В какую сторону они обуславливают отклонение искомого результата? Как можно снизить эти систематические погрешности?

3 Как Вы представляете различие между ближним и дальним порядком микрочастиц в конденсированных средах?

4. Решите задачу. В медный сосуд, нагретый до температуры t₁ = 350^оС, положили m₂ = 600 г льда при температуре t₂ = - 10^оС. В результате в сосуде оказалось m₃ = 550 г льда, смешанного с водой. Найти массу сосуда. Удельная теплоемкость меди С₁ = 420 .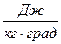

Литература:

1. В.Ф.Яковлев. Курс физики (теплота и молекулярная физика). М: 1976 г. §§ 2, 12, 87, 89.

2. А.К. Кикоин, И.К. Кикоин. Молекулярная физика. М.: 1976, § 129, 130.

3. Е.А. Штрауф. Молекулярная физика. М.-Л.: 1949, с. 493-500.

4. Р.В. Телеснин. Молекулярная физика. М.: 1973, §121, 122.

Экспериментальное определение универсальной газовой постоянной.

Цель работы: экспериментально определить значение универсальной газовой постоянной R, учитывая погрешность DR, сравнить полученный результат, с табличными данными. Оценить достоинства и недостатки предлагаемой работе.

Теоретическая часть:

Основные понятия.

Все тела — твердые, жидкие и газообразные — представляют собой совокупность большого числа атомов и молекул. При изучении свойств тел и физических явлений, происходящих с ними, возможны два метода исследований: термодинамический и молекулярно-кинетический:

- c помощью термодинамического метода изучаются свойства макросистем без учета молекулярных явлений, происходящих в них. При этом все процессы в макротелах или системах тел рассматриваются в основном с энергетической точки зрения. К примеру, Q = DИ+A – первое начало термодинамики;

- молекулярно-кинетический метод описывает состояния и законы протекания различных процессов в макротелах на основе изучения их молекулярной структуры и механизмов взаимодействия отдельных молекул между собой. Такие характеристики, как масса отдельных молекул, средняя скорость их движения, средняя энергия молекул и др., функционально увязываются с макроскопическими характеристиками тел (давление, температура и т. д.), которые можно определить непосредственно из опытов.

Оба метода тесно связаны между собой и взаимно дополняют друг друга.

Тело или совокупность макротел представляют собой термодинамическую систему. Состояние системы, в том числе и газа, определяется совокупностью ее свойств в заданный момент времени. Желательно в качестве таких свойств – характеристик выбрать такие величины, которые можно измерять опытным путем во время изменения состояния тела. Эти величины, характеризующие систему, называют параметрами состояния. К ним относятся масса, объем, давление, температура, сила и момент силы, напряженность электрического и магнитного полей и др. Систему принято называть простой, если ее состояние однозначно определяется параметрами: Р– давление, V– объем и Т– температура. При этом не всегда, но часто желательно, знать у изучаемой системы число молей или общую и молярную массу веществ, входящих в нее.

Параметры состояния системы делят на внешние и внутренние, экстенсивные и интенсивные. Внешние параметры – такие, значения которых зависят не только от самой системы, но и от внешних тел, взаимодействующих с системой (например, объем газа); внутренние – те параметры, значения которых определяются только системой (например, Р и Т). Экстенсивные параметры - это те, которым свойственна аддитивность (объем системы, ее масса, энергия и др.); интенсивные параметры одинаковы по макрочастям равновесной системы (к примеру, плотность в однофазной системе и др.).

Для простой системы уравнение состояния УС может быть задано функциями вида:

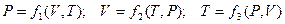
Универсальная газовая постоянная Rвходит в функциональную зависимость между параметрами одной из простых систем – идеальный газ. В молекулярной физике идеальный газ, как данность, рассматривают в двух вариантах:

- идеальный реальный газ – это газ, следующий уравнениям изопроцессов (законам Бойля-Мариотта, Шарля и Гей-Люссака), а также газ, для которого выполняются законы Дальтона и Авогадро.

Условиям соответствия реальному идеальному газу удовлетворяют Не, Н₂, N₂, О₂ и другие составляющие воздуха атмосферы планеты Земля. Исключение составляют те газы, которые достигают в интервале температур исследования состояния насыщения. Воздух, в котором 78% N₂, 21% О₂ и 0,95% инертных газов, хорошо удовлетворяет условиям идеального газа. Именно на воздухе и были установлены законы изопроцессов.

§2. Законы изопроцессов и уравнение Клапейрона (уравнение для любых реальных идеальных газов).

Для данной массы идеального газа (m = const) справедливы законы изопроцессов:

- изотермического (Т = const). Установлен в 1662 году Бойлем и Мариоттом.

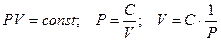
Графическое изображение изотермических процессов для отличающихся масс или температур представлено на рис. 1 и 2.

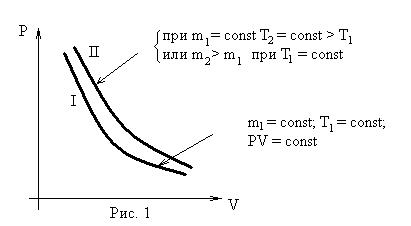
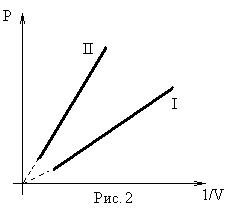
- изохорического (V = const). Установлен экспериментально в 1787 г. Гей-Люссаком (но носит имя президента французской академии наук того времени – Шарля):

по шкале Цельсияпо шкале Кельвина

Р = Р_о(1+b_оt)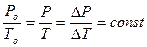

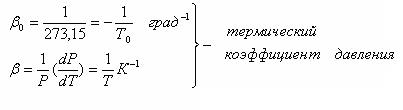Т_о = 273,15 К

Т = (Т_о + t⁰С)

- изобарического (Р = const). Установлен в 1802 году Гей-Люссаком, и носит его имя.

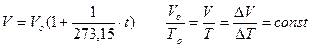
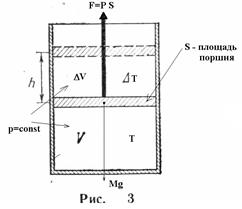
Пример: рисунок 3; DТ>0.

Масса газа в системе m = const

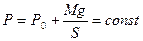
где: Р_о – атмосферное давление;

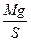- дополнительное давление поршня;

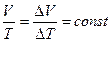
DV – изменение объема, соответствующее росту температуры в системе на DТ.

Этих законов изопроцессов достаточно, чтоб для любого реального идеального газа получить уравнение состояния (УС). С этой целью для некоторой массы газа выберем два совершенно произвольных состояния (в пределах идеальности):

1. (Р₁V₁Т₁); 2. (Р₂V₂T₂).

Переход из состояния 1®2 осуществим через промежуточное равновесное состояние 1^’ так, чтоб 1®1^’ принадлежали изотерме с конечным объемом V₂.

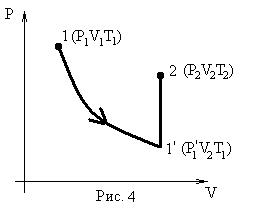
Р₁V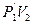₁ = (1)

Переход 1^’®2 осуществим по изохоре.

Для этого процесса:

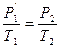(2)

Из уравнения (1) и (2) выразим :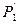

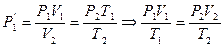
Т. к. состояние 1 и 2 были выбраны произвольно, то это значит, что для данной массы газа произведение давления на объем пропорционально абсолютной температуре:

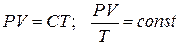(3)

Уравнения (3) и есть уравнения состояния идеального реального газа. Они получены Клапейроном (французским инженером и физиком, работавшим в институте инженеров путей сообщения) в 1834 году. (*! До введения абсолютной шкалы температур).