Измерения, их погрешности и обработка результатов измерений.
Лабораторный практикум
По молекулярной физике
Часть I
Архангельск
САФУ 2011
Методические рекомендации для студентов 1-го курса физического факультета ПГУ.
П о с в я щ а ю т с я
сыну и отцу физико-математического факультета
Дубровину
Павлу Васильевичу
(27 августа 1912 – 30 июля 1975)
Автор-составитель и редактор методических рекомендаций:
доцент кафедры общей физики Колпачников Г.Н.
Кафедра общей физики ПГУ имени М.В. Ломоносова.
Лаборатория механики и молекулярной физики.
 Группа __________ Фамилия И.О. студента ______________
Группа __________ Фамилия И.О. студента ______________
Содержание.
Стр.
Измерения, их погрешности и обработка результатов измерений. 4
Лабораторный практикум:
1. Определение удельной теплоты плавления льда
калориметрическим методом. 17
2.Определение универсальной газовой постоянной: R. 26
3.Определение отношения изобарической и изотермической теплоемкостей воздуха методом Клемана и Дезорма: Ср/СV. 40
4.Определение коэффициента внутреннего трения воздуха. 52
Автор-составитель искренне благодарен тем, кто принимал участие в постановке и модернизации работ практикума, в подготовке настоящих методических рекомендаций: Лазаревой О.В., Абикулову И.В., Тюкину Д.А., Михайлову И.Н., Орлову А.В. и др.
Таблица 1.
| … | n | средние значения | |||
| хi | 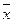 | ||||
Dхi= 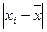 | 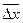 | ||||
| Приборная погрешность | Dхпр |
Вычисления:
Таблица 2.
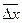 | s | ta,n | Dхсл | Dхпр | Абсолютная погрешность 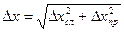 | Относительная погрешность 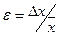 | |
| промежут. | |||||||
| конечная |
Итоговые данные прямых измерений могут быть представлены, как промежуточный, так и конечный результаты:
- результат принято считать промежуточным, если он будет использован в последующем для расчетов косвенно определяемой физической характеристики;
- в промежуточных данных желательно иметь одну запасную цифру. Разряд запасной цифры должен быть на один разряд ниже величин прямых измерений;
- промежуточный результат в абсолютной погрешности, как правило, содержит две цифры.
Нижний разряд погрешности и среднего значения результата измерений должны совпадать. Округление погрешности всегда проводится в сторону завышения, а результата измерений – по общим правилам (см. раздел II).
- практически общепринятой формой записи окончательного результата измерений принята следующая: а) в абсолютной погрешности сохраняется две значащих цифры, если первая из них 1 или 2, б) начиная с цифры 3, в погрешности сохраняется только одна значащая цифра.
Запись промежуточного и конечного результатов желательно сделать в рациональной форме, т.е. числом с единицами, десятыми и сотыми и другими долями и общим множителем.
10n. “n” – конечное целое число, но не желательно, чтоб оно принимало значения ±1.
Примеры:
1. (0,04528 ± 0,00073)ед. изм. Þ промежуточный результат = (4,528 ± 0,073)·10-2ед. изм. Þ конечный результат = (4,53 ± 0,08)·10-2 ед. изм.
2. Промежуточный результат; конечный результат
(45,22 ± 0,31) ед. изм. = (45,2 ± 0,4)ед. изм.
Правило 1.
Округление числа до значащих цифр достигается простым отбрасыванием неверных цифр, если первая из отбрасываемых цифр меньше, чем 5. Пример: 73,42Þ73,4; 73; 0,7×102;
Правило 2.
Если первая из отбрасываемых цифр больше, чем 5, то последняя оставленная цифра увеличивается на единицу. Последняя цифра увеличивается также и в том случае, когда первая из отбрасываемых цифр – 5, а за ней есть одна или несколько цифр, отличных от нуля. Пример: различные округления числа 35,856 Þ35,86; 35,9; 36.
Правило 3.
Если отбрасываемая цифра равна 5, а за ней нет значащих цифр, то округление производит на ближайшее четное число: последняя сохраняемая цифра остается неизменной, если она четная, и увеличивается на единицу, если она нечетная. Пример: округляем до двух значащих цифр: 0,435Þ0,44; 0,465Þ0,46.
При выполнении математических операций с числами важно учитывать два обстоятельства: значащие и запасные цифры; разряды тех цифр, с которыми выполняются операции.
1. При сложении и вычитании приближенных данных измерений в окончательном результате следует сохранить столько десятичных знаков, сколько их в приближенном числе с наименьшим числом десятичных знаков:
23,2+0,442+7,247 » 23,2+0,44+7,25 = 30,89 » 30,9
2. При умножении и делении в результате следует сохранить столько значащих цифр, сколько их имеет приближенное данное с наименьшим числом значащих цифр:
30,9 × 1,8364 » 30,9 · 1,84 = 56,856 » 56,9
56,9 : 2,412 » 56,9 : 2,41 = 23,609 » 23,6
3. При возведении в степень в результате следует сохранить столько значащих цифр, сколько их имеет возводимое в степень приближенное число:
(11,38)2 = 129,5044 » 129,5
4. При извлечении корня в результате следует сохранить столько значащих цифр, сколько их имеет подкоренное число:
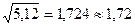
5. При нахождении логарифма приближенного числа нужно брать столько знаков, сколько верных знаков содержит данное число:
ln 77,23 » 2,8878 » 2,888
Примечание! При вычислении промежуточных результатов следует брать на одну цифру больше, чем указано в правилах округления при выполнении математических операций над числами. В окончательном результате эта “запасная” цифра отбрасывается. Приведенный ниже пример пояснит сказанное:
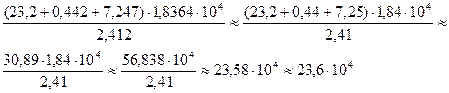
Таблица 4.
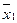 | Dх1сл | Dх1пр | 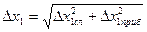 | … | 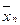 | Dхn сл | Dхn пр | 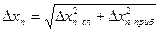 |
Если по обстоятельствам, обусловленным особенностями эксперимента, некоторый параметр хк измеряется однократно, то Dхк считается равным Dхк пр.
Абсолютная погрешность на постоянные множители, такие как p, g, r (плотность) и др. берется равной “±1”, к цифре самого низкого разряда: к примеру g= (9,816±0,001) м/с2 для Москвы (j=56о).
2. Расчет 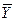 ведется на основе данных прямых измерений по промежуточным результатам и принятым табличным значениям постоянных коэффициентов:
ведется на основе данных прямых измерений по промежуточным результатам и принятым табличным значениям постоянных коэффициентов:
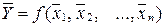
Некоторые числа и физические константы, используемые при расчетах:
p = 3,142; p2 = 9,870; 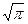 = 1,770; е = 2,718; lg е = 0,4343; ln 10 = 2,303.
= 1,770; е = 2,718; lg е = 0,4343; ln 10 = 2,303.
Расчетная формула ускорения силы тяжести для Земли в зависимости от широты места:
g = 9,78049 (1 + 0,00529·sinj) м/с2,
где j - широта места. Для Архангельска: j = 64о30’; sin 64о30’ = 0,9015
gАрх. = 9,78049·1,00477=9,8271 м/с2.
Таблица 5.
| №№ п/п | Физическая постоянная | Ее обозначение и значение |
| 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. | Гравитационная постоянная Число Авогадро Универсальная газовая постоянная Постоянная Больцмана Постоянная Планка Заряд электрона Масса покоя электрона Атомная единица массы Удельный заряд электрона Скорость света Лошадиная сила Земля: - масса - средний радиус Солнце: - масса - средний радиус Луна: - масса - средний радиус | g = 6,672·10-11 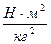 NА = 6,022·1023 моль-1 R = 8,314 NА = 6,022·1023 моль-1 R = 8,314  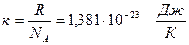 h = 6,625·10-34 Дж·с е = 1,602·10-19 Кл mе = 9,108·10-31 кг = 5,486 а.е.м. 1 а.е.м. = 1,660·10-27 кг h = 6,625·10-34 Дж·с е = 1,602·10-19 Кл mе = 9,108·10-31 кг = 5,486 а.е.м. 1 а.е.м. = 1,660·10-27 кг  = 1,759·1011 = 1,759·1011 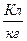 С = 2,998·108 м/с 1 л.с. = 735,5 Вт Мз = 5,976·1024 кг Rз = 6,37·106 м Мс = 1,97·1030 кг Rс = 6,96·108 м Мл = 7,35·1022 кг Rл = 1,72·106 кг С = 2,998·108 м/с 1 л.с. = 735,5 Вт Мз = 5,976·1024 кг Rз = 6,37·106 м Мс = 1,97·1030 кг Rс = 6,96·108 м Мл = 7,35·1022 кг Rл = 1,72·106 кг |
3. Для нахождения абсолютной погрешности косвенно измеренной величины желательно воспользоваться следующими рекомендациями:
- если искомая величина задана, как функция суммы (разности) несколько непосредственно измеренных величин или их достаточно простым произведением, то будет удобнее сразу же найти абсолютную погрешность DY. Расчетную формулу для DY легко получить, пользуясь методом дифференцирования, но, одновременно заменяя при этом:
- знаки дифференциала на знаки конечной погрешности;
- а знаки “минус” между слагаемыми на знаки “плюс” (погрешности только складываются!).
Пример: 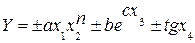 ,
,
-где a, b, c – некоторые константы, имеющие заведомо высокую точность,
- х1, х2, х3, х4 – величины прямого измерения с соответствующими абсолютными погрешностями Dх1, Dх2, Dх3, Dх4.
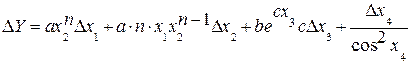
в) Если искомая характеристика задана произведением (включая и дробь) непосредственно измеренных величин, то вначале желательно рассчитать относительную погрешность e. Зная 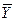 и e, можно найти и
и e, можно найти и 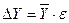 . Для получения расчетной формулы относительной погрешности e рекомендуем поступить так: прологарифмировать аналитическое выражение, а от него найти абсолютную погрешность,
. Для получения расчетной формулы относительной погрешности e рекомендуем поступить так: прологарифмировать аналитическое выражение, а от него найти абсолютную погрешность,
Пример: 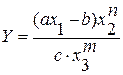 ; а, b, с – постоянные коэффициенты.
; а, b, с – постоянные коэффициенты.
1) 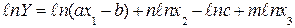 ;
;
2) 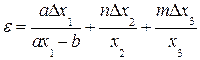 ;
;
3) 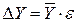
При окончательной записи результата косвенных измерений руководствуются теми же правилами, что и при прямых измерениях.
Заключение.
Завершив обработку данных и записав результаты эксперимента с указанием на абсолютную и относительную погрешности, сделайте окончательное суждение о:
- выполнимости проверяемого закона, правила или принципа (в частности, по интервалам перекрытия рассчитываемых характеристик);
- соответствии полученного результата различным модельным представлениям и табличным данным, приводимым в справочниках;
- необходимости, возможности и реальности учета систематических погрешностей метода;
- допущенных (не допущенных) промахах при прямых измерениях и выполненных расчетах;
- совершенствовании предложенного метода, а также использование других вариантов эксперимента.
Тригонометрические формулы
sin (x + y) = sin x cos y + sin y cos x. sin (x – y) = sin x cos y – sin y cos x.
cos (x + y) = cos x cos y – sin x sin y. cos (x – y) = cos x cos y + sin x sin y.
sin 2x = 2sin x cos y. cos 2x = cos2x – sin2x.
sin2x = ½(1 – cos 2x). cos2x = ½(1+cos 2x).
sin аx sin bx = ½ cos (a – b)x – ½ cos (a+b)x.
sin ax cos bx = ½ sin (a + b)x + ½ sin (a – b)x.
Расчеты.
Рекомендуем вначале сосчитать относительные приборные погрешности определения масс:
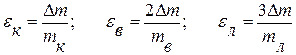
Есть основания полагать, что при взвешивании на электронных весах eк и eв малы (высокая степень точности). Погрешность на лед Dmл=3Dm учитывается дважды и, видимо, ее придется учесть. В этом случае желательно вначале провести расчет lрасч. По формуле (12) без учета водяного эквивалента термометра, затем найти e по (13) и, наконец, Dl.
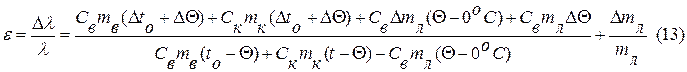
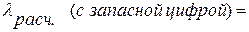
e =
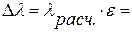
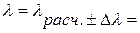
Расчеты и выводы:
Контрольные вопросы:
1. Сформулируйте начала термодинамики, используемые в проведенном эксперименте. В каком варианте они применимы?
2. Какие виды систематических погрешностей имеют место в предложенном методе определения lпл льда? В какую сторону они обуславливают отклонение искомого результата? Как можно снизить эти систематические погрешности?
3 Как Вы представляете различие между ближним и дальним порядком микрочастиц в конденсированных средах?
4. Решите задачу. В медный сосуд, нагретый до температуры t1 = 350оС, положили m2 = 600 г льда при температуре t2 = - 10оС. В результате в сосуде оказалось m3 = 550 г льда, смешанного с водой. Найти массу сосуда. Удельная теплоемкость меди С1 = 420  .
.
Литература:
1. В.Ф.Яковлев. Курс физики (теплота и молекулярная физика). М: 1976 г. §§ 2, 12, 87, 89.
2. А.К. Кикоин, И.К. Кикоин. Молекулярная физика. М.: 1976, § 129, 130.
3. Е.А. Штрауф. Молекулярная физика. М.-Л.: 1949, с. 493-500.
4. Р.В. Телеснин. Молекулярная физика. М.: 1973, §121, 122.
Экспериментальное определение универсальной газовой постоянной.
Цель работы: экспериментально определить значение универсальной газовой постоянной R, учитывая погрешность DR, сравнить полученный результат, с табличными данными. Оценить достоинства и недостатки предлагаемой работе.
Теоретическая часть:
Основные понятия.
Все тела — твердые, жидкие и газообразные — представляют собой совокупность большого числа атомов и молекул. При изучении свойств тел и физических явлений, происходящих с ними, возможны два метода исследований: термодинамический и молекулярно-кинетический:
- c помощью термодинамического метода изучаются свойства макросистем без учета молекулярных явлений, происходящих в них. При этом все процессы в макротелах или системах тел рассматриваются в основном с энергетической точки зрения. К примеру, Q = DИ+A – первое начало термодинамики;
- молекулярно-кинетический метод описывает состояния и законы протекания различных процессов в макротелах на основе изучения их молекулярной структуры и механизмов взаимодействия отдельных молекул между собой. Такие характеристики, как масса отдельных молекул, средняя скорость их движения, средняя энергия молекул и др., функционально увязываются с макроскопическими характеристиками тел (давление, температура и т. д.), которые можно определить непосредственно из опытов.
Оба метода тесно связаны между собой и взаимно дополняют друг друга.
Тело или совокупность макротел представляют собой термодинамическую систему. Состояние системы, в том числе и газа, определяется совокупностью ее свойств в заданный момент времени. Желательно в качестве таких свойств – характеристик выбрать такие величины, которые можно измерять опытным путем во время изменения состояния тела. Эти величины, характеризующие систему, называют параметрами состояния. К ним относятся масса, объем, давление, температура, сила и момент силы, напряженность электрического и магнитного полей и др. Систему принято называть простой, если ее состояние однозначно определяется параметрами: Р– давление, V– объем и Т– температура. При этом не всегда, но часто желательно, знать у изучаемой системы число молей или общую и молярную массу веществ, входящих в нее.
Параметры состояния системы делят на внешние и внутренние, экстенсивные и интенсивные. Внешние параметры – такие, значения которых зависят не только от самой системы, но и от внешних тел, взаимодействующих с системой (например, объем газа); внутренние – те параметры, значения которых определяются только системой (например, Р и Т). Экстенсивные параметры - это те, которым свойственна аддитивность (объем системы, ее масса, энергия и др.); интенсивные параметры одинаковы по макрочастям равновесной системы (к примеру, плотность в однофазной системе и др.).
Для простой системы уравнение состояния УС может быть задано функциями вида:
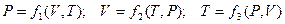
Универсальная газовая постоянная Rвходит в функциональную зависимость между параметрами одной из простых систем – идеальный газ. В молекулярной физике идеальный газ, как данность, рассматривают в двух вариантах:
- идеальный реальный газ – это газ, следующий уравнениям изопроцессов (законам Бойля-Мариотта, Шарля и Гей-Люссака), а также газ, для которого выполняются законы Дальтона и Авогадро.
Условиям соответствия реальному идеальному газу удовлетворяют Не, Н2, N2, О2 и другие составляющие воздуха атмосферы планеты Земля. Исключение составляют те газы, которые достигают в интервале температур исследования состояния насыщения. Воздух, в котором 78% N2, 21% О2 и 0,95% инертных газов, хорошо удовлетворяет условиям идеального газа. Именно на воздухе и были установлены законы изопроцессов.
§2. Законы изопроцессов и уравнение Клапейрона (уравнение для любых реальных идеальных газов).
Для данной массы идеального газа (m = const) справедливы законы изопроцессов:
- изотермического (Т = const). Установлен в 1662 году Бойлем и Мариоттом.
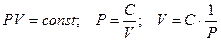
Графическое изображение изотермических процессов для отличающихся масс или температур представлено на рис. 1 и 2.
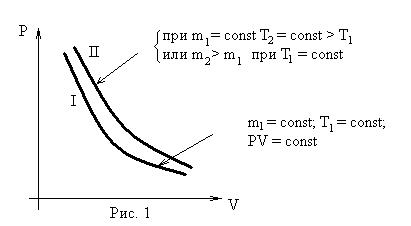
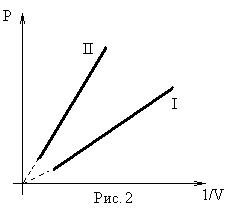
- изохорического (V = const). Установлен экспериментально в 1787 г. Гей-Люссаком (но носит имя президента французской академии наук того времени – Шарля):
по шкале Цельсияпо шкале Кельвина
Р = Ро(1+bоt) 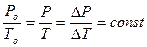
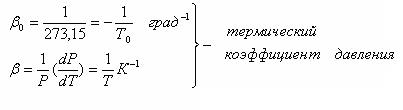 То = 273,15 К
То = 273,15 К
Т = (То + t0С)
- изобарического (Р = const). Установлен в 1802 году Гей-Люссаком, и носит его имя.
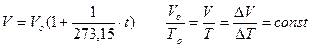
Пример: рисунок 3; DТ>0.
Масса газа в системе m = const
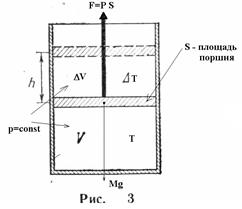 где: Ро – атмосферное давление;
где: Ро – атмосферное давление;
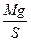 - дополнительное давление поршня;
- дополнительное давление поршня;
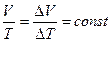
DV – изменение объема, соответствующее росту температуры в системе на DТ.
Этих законов изопроцессов достаточно, чтоб для любого реального идеального газа получить уравнение состояния (УС). С этой целью для некоторой массы газа выберем два совершенно произвольных состояния (в пределах идеальности):
1. (Р1V1Т1); 2. (Р2V2T2).
Переход из состояния 1®2 осуществим через промежуточное равновесное состояние 1’ так, чтоб 1®1’ принадлежали изотерме с конечным объемом V2.
Р1V1 =  (1)
(1)
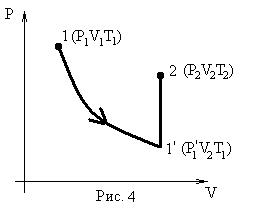
Переход 1’®2 осуществим по изохоре.
Для этого процесса:
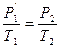 (2)
(2)
Из уравнения (1) и (2) выразим 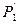 :
:
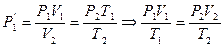
Т. к. состояние 1 и 2 были выбраны произвольно, то это значит, что для данной массы газа произведение давления на объем пропорционально абсолютной температуре:
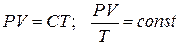 (3)
(3)
Уравнения (3) и есть уравнения состояния идеального реального газа. Они получены Клапейроном (французским инженером и физиком, работавшим в институте инженеров путей сообщения) в 1834 году. (*! До введения абсолютной шкалы температур).
Таблица 1.
| № | mо, г | mi, г | (mi – mо), г | Dр=(Рл – Рi) кс/см2 Па | Т | Ri | DRi | ||
| 1. 2. 3. | |||||||||
| ср. значен. | |||||||||
Расчеты и выводы:
! Оцените скорость натекания воздуха в систему.
Теоретическое введение
Таблица 2.
| Процессы | А | Du | Q | Теплоемкость | |
| Сх | Схm | ||||
V=сonst (dV=0) 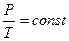 P=cT P=cT | 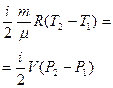 | Qv=Du | 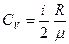 | 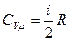 | |
P = const (dP = 0) 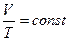 V = сТ V = сТ | 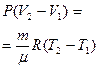 | 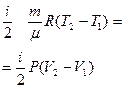 | 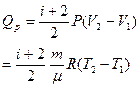 | 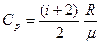 | 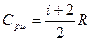 |
| T = const (dT = 0) PV = const | 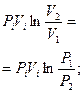 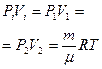 | Qт = Ат | ±¥ | ±¥ |
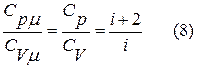
О воздухе.
Сухой воздух содержит: 78,1 % азота – N2; 21,0 % кислорода – О2; 0,94 % инертных газов – He, Ne и др.; 0,03 % СО2 и в небольшом количестве других газов.
1. Средняя молярная масса воздуха:
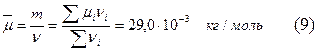
2. Среднее число степеней свободы молекул воздуха в широком температурном интервале практически совпадает с числом степеней свободы у жестких 2-х атомных молекул (их в воздухе чуть более 99 %).
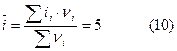
В приведенных соотношениях:
m – масса рассматриваемой системы,
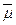 - средняя молярная масса смеси газов,
- средняя молярная масса смеси газов,
ni – число молей (количество вещества) i –го газа;
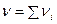 - общее количество вещества в системе, выраженное в молях;
- общее количество вещества в системе, выраженное в молях;
ii – число степеней свободы у молекул i – го газа;
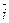 - среднее число степеней свободы для молекул смеси газов (многокомпонентной газовой системы).
- среднее число степеней свободы для молекул смеси газов (многокомпонентной газовой системы).
3. Средние значения молярных и удельных теплоемкостей:
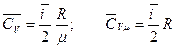
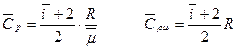
Тогда в модельном представлении о воздухе, как идеальном газе из жестких молекул, отношение изобарической и изохорической теплоемкостей, обозначаемое gравно:
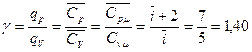
4. Реальный воздух влажный. Он содержит пары воды. Молекулы воды в газообразном состоянии, как пространственные жесткие, обладают 6-ю степенями свободы. При температуре 25оС и влажности 65 % доля молекул воды в воздухе не превышает 1,0 %. В отношении среднего значения степеней свободы у молекул такого воздуха это своеобразная компенсация присутствия в нем примерно такой же доли одноатомных молекул инертных газов (i = 3). Поэтому водяной пар, не конденсирующийся в эксперименте, дополнительно приближает среднее число степеней свободы молекул воздуха к пяти ( 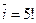 ).
).
Таблица 3.
| Уравнение процесса | Характерный показатель | Структура молекул | ||
| 1 атомн. | 2-х атомн. и линейные многоатомные | Пространственные многоатомные | ||
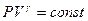 | 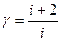 | 1,67 | 1,40 | 1,33 |
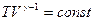 | 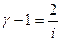 | 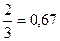 | 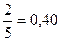 | 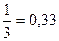 |
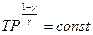 | 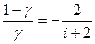 | - 0,40 | - 0,29 | - 0,25 |
* При построении помните, что адиабатное сжатие идеального газа сопровождается ростом давления и температуры. Причем давление растет при сжатии быстрее, чем по линейному закону. Крутизна Р(Т) зависит от структуры молекул.
Таблица 4.
| n | ±¥ | 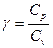 | ||
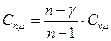 | 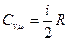 | 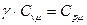 | ±¥ | |
| Термическое уравнение процесса | 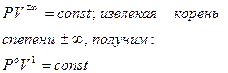 V = const V = const | P = const | PV= =const | 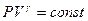 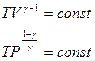 |
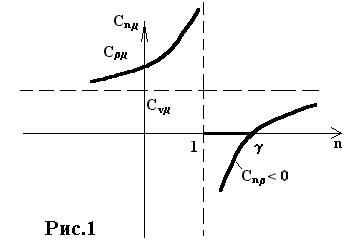 Важно отметить, что в интервале значений показателя политропы от 1 до g,теплоемкость системы отрицательна:
Важно отметить, что в интервале значений показателя политропы от 1 до g,теплоемкость системы отрицательна:
- при теплоподводе температура понижается;
- при теплоотводе Т растет.
Таблица
данных прямых измерений и расчета  и
и 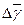 .
.
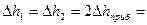
| № | h1; л мм | h1; п | h1 мм | Dh2; л мм | h2; п мм | h2 мм | gi | Dgi |
| … | ||||||||
| средние арифметические значения |
4. Расчет случайной погрешности 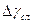 проведите по методике прямых многократных измерений, полагая доверительность интервала значений равной 90 %.
проведите по методике прямых многократных измерений, полагая доверительность интервала значений равной 90 %.
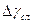 =
=
Замечания-рекомендации:
1. Так как при выводе формулы (6.4) считали температуру воздуха в состоянии 1 равной температуре окружающей среды, а процесс 1®2 адиабатным, то эти условия – требования надо по возможности выполнить:
а) h1 и h2 определять только тогда, когда уровни жидкости в коленах манометра установились (Т1 = Токр.среды). Ясно, что при этом все контакты, через которые воздух в сосуде может быть соединен с окружающим воздухом, должны быть исключены (натекание легко фиксируется по постоянному изменению уровней в манометре).
* Метод Клемана-Дезорма допускает определение g и в ситуации, когда в системе в начальном состоянии создается повышенное давление. Но в этом случае сконструировать закрытую систему труднее. Почему?
б) процесс 1®2 надо осуществить быстро, практически исключив теплообмен через стеклянные стенки сосуда, но, безусловно, полностью (соблюсти это условие невозможно). С этой целью:
- кран К2, имеющий достаточно большое отверстие для сообщения с атмосферой, открывать на максимальное сечение;
- факт выравнивания давлений в сосуде и атмосфере фиксировать не по манометру (он инерционен), а по звуковому эффекту.
Субъективность звукового восприятия очевидна. Если закрыть кран раньше выравнивания давлений, то это приведет к завышению h2 и g (свойственно экспериментаторам с пониженным слухом). Запоздать – скажется эффект теплообмена, что приведет к занижению h2 и экспериментально найденного g. Поэтому предлагается:
- провести пробный эксперимент (2¸3 раза) и по полученным значениям g постараться понять причины отклонения результата от теоретически ожидаемого;
- результатов по gI иметь 10¸15. Так удается снизить случайную погрешность Dgсл.
1. Обращаем ваше внимание на осторожность выполнения операции по разряжению воздуха в системе и приведение его в состояние 1. Делать это надо аккуратно и достаточно медленно. В противном случае манометрическая жидкость может быть втянута в стеклянный сосуд.
Это чревато двумя негативными обстоятельствами:
- в системе будет находиться конденсат и насыщенный пар воды. Это исказит результат эксперимента. Почему и как?;
- манометр придется отсоединять от системы и наполнять манометрической жидкостью, а систему в целом сушить.
2. Выбор интервала возможных и приемлемых значений h1 проведите с учетом приборной погрешности, звукового эффекта, приближенности процесса 1®2 к адиабатному, а также пределов измерений, допустимых для манометра. С этой целью и предлагается 2÷3 пробных эксперимента.
Погрешности:
1. Dgсл определяется с учетом 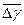 и доверительности интервала значений.
и доверительности интервала значений.
2. 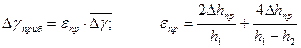
3. 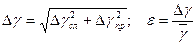
4. Для оценки величин, характеризующих систематическую погрешность, предлагается поступить так:
- дважды в последовательности создать в системе одинаковые разряжения, близкие к максимально возможному значению h1, но ни в коем случае не допускать переливания манометрической жидкости;
- в первом случае определить время звукового сигналаtзв;
- во втором случае определяется возникающая разность показаний манометра сразу после закрытия крана К2(в процессе 2®3) за время звукового сигнала (за tзв) – h3.
- тогда за относительную погрешность, обусловленную теплообменом eт.обм. можно оценочно принять 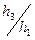 ; а значение систематической погрешности на
; а значение систематической погрешности на 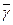 оценить, как
оценить, как 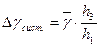 .
.
* Т. к. tзв мало, то, допустив теплообмен вначале 2®3 постоянным, можно определить h3 за время в 10 раз больше - 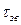 *. Тогда
*. Тогда
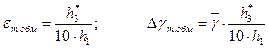
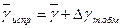
Расчеты и выводы:
Контрольные вопросы:
1. Внутренняя энергия идеального газа: возможные составляющие. Теорема Больцмана о средней энергии на различные степени свободы. Внутренняя энергия жестких молекул различной структуры.
2. Изопроцессы с идеальным газом (включая адиабатный и политропический): их термическое и калорическое описание; графики процессов в различных координатах (выбор двух из следующих: Р, V, Т, r, Сv, Ср, u).
3. Внутренняя энергия и теплоемкости воздуха в различных изопроцессах.
4. Может ли быть теплоемкость системы отрицательной? Есть ли такой процесс в выполняемой лабораторной работе?
5. Систематические погрешности, возможность их учета и устранения.
6. Зачем сосуды обклеены фольгой?
Литература:
1. В.Ф. Яковлев. Курс физики (теплота и молекулярная физика) М., “Просвещение”, 1976 г, §§ 7-9, 18-24, 37.
2. А.К. Кикоин, И.К. Кикоин. Молекулярная физика. М., “Наука”, 1976 г., §§ 26-34.
3. Р.В. Телеснин. Молекулярная физика. М., “Высшая школа”, 1973 г., §§ 27-30, 33-40.
4. Д.В. Сивухин. Общий курс физики, т.2. М. 1975, §§ 20-24.
Определение коэффициента
Внутреннего трения воздуха.
Цель работы: по данным прямых измерений характеристик, определяющих направленное течение воздуха по капилляру (игле шприца), рассчитать h, 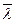 и dэф этой среды.
и dэф этой среды.
Явления переноса

 К явлениям переноса в курсе молекулярной физики относят группу процессов, происходящих в системах, не находящихся в равновесном состоянии и имеющих неоднородность по одной или нескольким характеристикам (к примеру, плотности, температуре или скорости упорядоченного (направленного) движения).
К явлениям переноса в курсе молекулярной физики относят группу процессов, происходящих в системах, не находящихся в равновесном состоянии и имеющих неоднородность по одной или нескольким характеристикам (к примеру, плотности, температуре или скорости упорядоченного (направленного) движения).
При наличии неоднородности:
по плотности или концентрации данного вещества ( 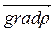 или
или 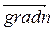 ) в системе наблюдается перенос вещества, т.е. явление диффузии;
) в системе наблюдается перенос вещества, т.е. явление диффузии;
по температуре ( 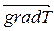 ) имеет место передача внутренней энергии, т.е. явление теплопроводности;
) имеет место передача внутренней энергии, т.е. явление теплопроводности;
в распределении молекул по скоростям направленного движения ( 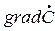 ): С - скорость направленного движения. В этом случае происходит передача импульса и механической энергии упорядоченного движения, от слоя с большей скоростью направленного движения, к слою с меньшей скоростью этого движения. Изменению импульса за единицу времени соответствует сила, которую и называют силой внутреннего трения (вязкостью).
): С - скорость направленного движения. В этом случае происходит передача импульса и механической энергии упорядоченного движения, от слоя с большей скоростью направленного движения, к слою с меньшей скоростью этого движения. Изменению импульса за единицу времени соответствует сила, которую и называют силой внутреннего трения (вязкостью).
Явления переноса проявляются в том, что в среде возникает направленный перенос массы (диффузия), импульса направленного движения (внутреннее трение) и внутренней энергии (теплопроводность).
§1. Феноменологическое описание явлений переноса
Диффузия
Диффузией называют явление, обусловленное тепловым движением молекул одних веществ в объём, занятый другими веществами. В химически чистых газах при постоянной температуре диффузия возникает вследствие неод
