Режим электромагнитного тормоза

Этот режим работы наступает, если ротор и магнитное поле вращаются в разные стороны. Этот режим работы имеет место при реверсе асинхронного двигателя, когда изменяют порядок чередования фаз, т.е. изменяется направление вращения магнитного поля, а ротор по инерции вращается в прежнем направлении.

Согласно рис. 2.11 электромагнитная сила будет создавать тормозной электромагнитный момент, под действием которого будет снижаться частота вращения ротора, а затем произойдёт реверс.

В режиме электромагнитного тормоза машина потребляет механическую энергию, развивая на валу тормозной момент, и одновременно потребляет из сети электрическую энергию. Вся эта энергия идёт на нагрев машины.

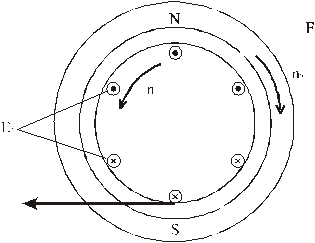
Рис.2.11

При n=n0,S=1.

При n→−∞,S→+∞.

Таким образом, в режиме электромагнитного тормоза скольжение изменяется в пределах:

0<S<∞.

Процессы в асинхронной машине

Цепь статора

а) ЭДС статора.

Магнитное поле, создаваемое обмоткой статора, вращается относительно неподвижного статора с частотой n0=60f)/p и будет наводить в обмотке статора ЭДС. Действующее значение ЭДС, наводимой этим полем в одной фазе обмотки статора определяется выражением:

E1=4,44w1k1fΦ,

где: k1=0.92÷0.98 – обмоточный коэффициент;
f1=f – частота сети;
w1 – число витков одной фазы обмотки статора;
Φ – результирующее магнитное поле в машине.

б) Уравнение электрического равновесия фазы обмотки статора.

Это уравнение составлено по аналогии с катушкой с сердечником, работающей на переменном токе.

.

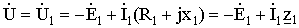Здесь Ú и Ú1 – напряжение сети и напряжение, подведённое к обмотке статора.
R1 – активное сопротивление обмотки статора, связанное с потерями на нагрев обмотки.
x1 – индуктивное сопротивление обмотки статора, связанное с потоком рассеяния.
z1 – полное сопротивление обмотки статора.
İ1 – ток в обмотке статора.

При анализе работы асинхронных машин часто принимают I1z1=0. Тогда можно записать:

U1≈E1=4,44w1k1fΦ.

Из этого выражения следует, что магнитный поток Φ в асинхронной машине не зависит от её режима работы, а при заданной частоте сети f зависит только от действующего значения приложенного напряжения U1. Аналогичное соотношение имеет место и в другой машине переменного тока – в трансформаторе.

Цепь ротора

а) Частота ЭДС и тока ротора.

При неподвижном роторе частота ЭДС f2 равна частоте сети f.

f2=f=(n0p)/60.

При вращающемся роторе частота ЭДС ротора зависит от частоты вращения магнитного поля относительно вращающегося ротора, которая определяется соотношением:

n'=n0−n.

Тогда частота ЭДС вращающегося ротора:

.

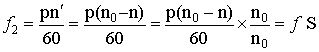Частота ЭДС ротора изменяется пропорционально скольжению и в режиме двигателя имеет наибольшее значение в момент пуска в ход.

Пусть при f=50Гц, номинальное скольжение Sн=2%. Тогда при номинальной частоте вращения ротора f2=f×Sн=1Гц.

Таким образом, в обмотке ротора асинхронной машины частота наводимой ЭДС зависит от частоты вращения ротора.

б) ЭДС ротора.

При неподвижном роторе f2=f и действующее значение ЭДС определяется по аналогии с E1.

E2=4,44w2k2fΦ,

где: w2 и k2 – соответственно число витков и обмоточный коэффициент обмотки ротора.

Если ротор вращается, то f2=f×Sн и ЭДС вращающегося ротора определяется соотношением:

E2S=4,44w2k2f2Φ=E2S.

ЭДС, наводимая в обмотке ротора, изменяется пропорционально скольжению и в режиме двигателя имеет наибольшее значение в момент пуска в ход.

Отношение ЭДС статора к ЭДС неподвижного ротора называется коэффициентом трансформации асинхронной машины.

k=	E1	=	w1k1	.
E2	w2k2

в) ток ротора.

Запишем уравнение равновесия для одной фазы короткозамкнутого ротора.

При неподвижном роторе.

,

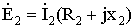где: x2=2πfL2 – индуктивное сопротивление обмотки неподвижного ротора, связанное с потоком рассеяния;
R2 – активное сопротивление обмотки ротора, связанное с потерями на нагрев обмотки.

При вращающемся роторе.

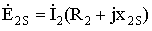
где: x2S=2πf2L2=2πfL2S=x2S – индуктивное сопротивление обмотки вращающегося ротора.

Для тока ротора в общем случае можно получить такое соотношение:

.

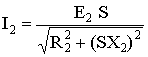Отсюда следует, что ток ротора зависит от скольжения и возрастает при его увеличении, но медленнее, чем ЭДС.

г) поле ротора

Обмотка ротора, как и обмотка статора, является многофазной и при появлении в ней тока создаёт своё вращающееся магнитное поле. Обозначим через n2 частоту вращения магнитного поля ротора относительно ротора.

n2=(60f2)/p=(60fS)/p.

Здесь p – число пар полюсов обмотки ротора, оно всегда равно числу пар полюсов обмотки статора.

Относительно статора магнитное поле ротора вращается с частотой

.

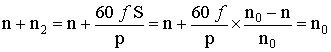Из полученного соотношения следует, что магнитное поле ротора относительно статора вращается с той же частотой, что и магнитное поле статора. Таким образом, магнитные поля ротора и статора относительно друг друга неподвижны. Поэтому при анализе работы асинхронной машины можно применить те же соотношения, что и трансформаторе.

Ток статора

Так как результирующее магнитное поле асинхронной машины не зависит от её режима работы, можно составить для одной фазы уравнение магнитодвижущих сил, приравняв магнитодвижущую силу в режиме холостого хода к сумме магнитодвижущих сил в режиме нагрузки.

İ0w1k1=İ1w1k1+İ2w2k2

Отсюда İ1=İ0+İ'2.

Здесь I0 – ток в обмотке статора в режиме идеального холостого хода, I'2=−I2(w2k2)/(w1k1) – составляющая тока статора, которая компенсирует действие магнитодвижущей силы обмотки ротора. Полученное выражение для тока статора отражает свойство саморегулирования асинхронной машины. Чем больше ток ротора, тем больше ток статора. В режиме холостого хода ток статора минимальный. В режиме нагрузки ток статора возрастает. Ток реального холостого хода асинхронной машины I0=(20÷60)%I1н и значительно больше по сравнению с номинальным током, чем у трансформатора. Это объясняется тем, что величина тока I0 зависит от магнитного сопротивления среды, в которой создаётся магнитное поле. У асинхронной машины, в отличие от трансформатора, есть воздушный зазор, который создаст большое сопротивление магнитному полю.