Элементы квантовой физики атомов, молекул и твердых тел
 27
27
ТЕОРИЯ АТОМА ВОДОРОДА ПО БОРУ
§ 208. Модели атома Томсона и Резерфорда
Представление об атомах как неде- лимых мельчайших частицах вещества («атомос» — неразложимый) возникло еще в античные времена (Демокрит, Эпикур, Лукреций). К началу XVIII в. атомистическая теория приобретает все большую популярность, так как к это- му времени в работах А.Лавуазье1, М.В.Ломоносова и Д.Дальтона была доказана реальность существования атомов. Однако в это время вопрос о внутреннем строении атомов даже не возникал, так как атомы по-прежнему считались неделимыми.
 Большую роль в развитии атомисти- ческой теории сыграл
Большую роль в развитии атомисти- ческой теории сыграл  разработавший в 1869 г. Периодиче- скую систему элементов, в которой впервые научной основе был постав- лен вопрос о единой природе атомов. Во второй половине XIX в. экспери- ментально было доказано, что электрон является одной из основных составных частей любого вещества. Эти выводы, а также экспериментальные данные при-
разработавший в 1869 г. Периодиче- скую систему элементов, в которой впервые научной основе был постав- лен вопрос о единой природе атомов. Во второй половине XIX в. экспери- ментально было доказано, что электрон является одной из основных составных частей любого вещества. Эти выводы, а также экспериментальные данные при-
А. Лавуазье (1743 — 1794) —  хи- мик.
хи- мик.
вели к тому, что в начале XX в. серьез- но встал вопрос о строении атома.
Первая попытка создания на осно- ве накопленных экспериментальных данных модели атома принадлежит Дж. Дж. Томсону (1903). Согласно этой модели, атом представляет собой непре- рывно заряженный положительным за- рядом шар радиусом порядка 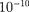 м, внутри которого около своих положе- ний равновесия колеблются электроны; суммарный отрицательный заряд элек- тронов равен положительному заряду шара, поэтому атом в целом нейтрален. Через несколько лет было доказано, что представление о непрерывно распреде- ленном внутри атома положительном заряде ошибочно.
м, внутри которого около своих положе- ний равновесия колеблются электроны; суммарный отрицательный заряд элек- тронов равен положительному заряду шара, поэтому атом в целом нейтрален. Через несколько лет было доказано, что представление о непрерывно распреде- ленном внутри атома положительном заряде ошибочно.
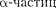
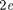 В развитии представлений о строе- нии атома велико значение опытов анг- лийского физика Э. Резерфорда (1871 — 1937)по рассеянию в веще- стве. Альфа-частицы возникают при радиоактивных превращениях; они яв- ляются положительно заряженными частицами с зарядом и массой, при- мерно в 7300 раз большей массы элект- рона. Пучки а-частиц обладают высо- кой монохроматичностью [для данного превращения имеют практически одну и ту же скорость (порядка 107м/с)].
В развитии представлений о строе- нии атома велико значение опытов анг- лийского физика Э. Резерфорда (1871 — 1937)по рассеянию в веще- стве. Альфа-частицы возникают при радиоактивных превращениях; они яв- ляются положительно заряженными частицами с зарядом и массой, при- мерно в 7300 раз большей массы элект- рона. Пучки а-частиц обладают высо- кой монохроматичностью [для данного превращения имеют практически одну и ту же скорость (порядка 107м/с)].
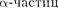 Э. Резерфорд, исследуя прохождение в веществе (через золотую
Э. Резерфорд, исследуя прохождение в веществе (через золотую
 фольгу толщиной примерно 1 мкм), по- казал, что основная их часть испытыва- ет незначительные отклонения, но неко- торые (примерно одна из 20 000) резко отклоняются от первона- чального направления (углы отклоне- ния достигали даже 180°).
фольгу толщиной примерно 1 мкм), по- казал, что основная их часть испытыва- ет незначительные отклонения, но неко- торые (примерно одна из 20 000) резко отклоняются от первона- чального направления (углы отклоне- ния достигали даже 180°). 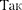 как элек- троны не могут существенно изменить движение столь тяжелых и быстрых ча- стиц, как а-частицы, то Резерфордом был сделан вывод, что значительное от- клонение а-частиц обусловлено их вза- имодействием с положительным заря- дом большой массы. Однако значитель- ное отклонение испытывают лишь не- многие а-частицы; следовательно, лишь некоторые из них проходят вблизи дан- ного положительного заряда. Это, в свою очередь, означает, что положительный заряд атома сосредоточен в объеме, очень малом по сравнению с объемом атома.
как элек- троны не могут существенно изменить движение столь тяжелых и быстрых ча- стиц, как а-частицы, то Резерфордом был сделан вывод, что значительное от- клонение а-частиц обусловлено их вза- имодействием с положительным заря- дом большой массы. Однако значитель- ное отклонение испытывают лишь не- многие а-частицы; следовательно, лишь некоторые из них проходят вблизи дан- ного положительного заряда. Это, в свою очередь, означает, что положительный заряд атома сосредоточен в объеме, очень малом по сравнению с объемом атома.
На основании своих исследований Резерфорд в 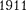 г. предложил ядер- ную {планетарную) модель атома. Согласно этой модели, вокруг положи- тельного ядра, имеющего заряд Ze
г. предложил ядер- ную {планетарную) модель атома. Согласно этой модели, вокруг положи- тельного ядра, имеющего заряд Ze 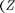 — порядковый номер элемента в системе Менделеева, е — элементарный заряд), размер
— порядковый номер элемента в системе Менделеева, е — элементарный заряд), размер 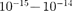 м и массу, практи- чески равную массе атома, в области с линейными размерами порядка
м и массу, практи- чески равную массе атома, в области с линейными размерами порядка 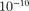 м по замкнутым орбитам движутся элек- троны, образуя электронную оболочку атома. Так как атомы нейтральны, то за- ряд ядра равен суммарному заряду электронов, т.е. вокруг ядра должно вращаться Z электронов.
м по замкнутым орбитам движутся элек- троны, образуя электронную оболочку атома. Так как атомы нейтральны, то за- ряд ядра равен суммарному заряду электронов, т.е. вокруг ядра должно вращаться Z электронов.
Для простоты предположим, что электрон движется вокруг ядра по кру- говой орбите радиусом г. При этом ку- лоновская сила 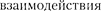 между ядром и электроном сообщает электро- ну нормальное ускорение. Уравнение, описывающее движение электрона в
между ядром и электроном сообщает электро- ну нормальное ускорение. Уравнение, описывающее движение электрона в
атоме по окружности под ку- лоновской силы:
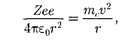
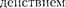 (208.1)
(208.1)
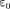
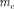 где — электрическая постоянная;
где — электрическая постоянная;
 v — масса и скорость электрона на ор- бите радиусом г.
v — масса и скорость электрона на ор- бите радиусом г.
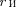
 Уравнение (208.1) содержит два не- известных: v. Следовательно, суще- ствует бесчисленное множество значе- ний радиуса и соответствующих ему значений скорости (а значит, и энер- гии), удовлетворяющих этому уравне- нию. Поэтому величины v (следова- тельно, и Е) могут меняться непрерыв- но, т. е. может испускаться любая, а не вполне определенная порция энергии. Тогда спектры атомов должны быть сплошными. В действительности же опыт показывает, что атомы имеют ли- нейчатый спектр.
Уравнение (208.1) содержит два не- известных: v. Следовательно, суще- ствует бесчисленное множество значе- ний радиуса и соответствующих ему значений скорости (а значит, и энер- гии), удовлетворяющих этому уравне- нию. Поэтому величины v (следова- тельно, и Е) могут меняться непрерыв- но, т. е. может испускаться любая, а не вполне определенная порция энергии. Тогда спектры атомов должны быть сплошными. В действительности же опыт показывает, что атомы имеют ли- нейчатый спектр.
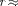 Из выражения (208.1) следует, что при 10~10 м скорость движения элек-
Из выражения (208.1) следует, что при 10~10 м скорость движения элек-
о
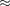
 тронов v
тронов v 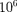 м/с, а ускорение — — 1022 м/с2. Согласно классической элек- тродинамике, ускоренно движущиеся электроны должны излучать электро-
м/с, а ускорение — — 1022 м/с2. Согласно классической элек- тродинамике, ускоренно движущиеся электроны должны излучать электро-
магнитные волны и вследствие этого не- прерывно терять энергию. В результате электроны будут приближаться к ядру и в конце концов упадут на него. Таким образом, атом Резерфорда оказывается неустойчивой системой, что опять-таки противоречит действительности.
Попытки построить модель атома в рамках классической физики не приве- ли к успеху: модель Томсона была оп- ровергнута опытами Резерфорда, ядер- ная же модель оказалась неустойчивой электродинамически и противоречила опытным данным. Преодоление воз- никших трудностей потребовало созда- ния качественно новой — квантовой — теории атома.
§ 209. Линейчатый спектр атома водорода
Исследования спектров излучения разреженных газов (спектров излу- чения отдельных атомов) показали, что каждому газу присущ определен- ный линейчатый спектр, состоящий из отдельных спектральных линий или групп близко расположенных линий. Самым изученным является спектр наиболее простого атома — атома водо- рода.
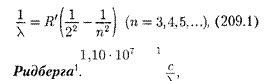 Швейцарский ученый И. Бальмер (1825— 1898) подобрал эмпирическую формулу, описывающую все известные в то время спектральные линии атома водорода в видимой области спектра:
Швейцарский ученый И. Бальмер (1825— 1898) подобрал эмпирическую формулу, описывающую все известные в то время спектральные линии атома водорода в видимой области спектра:
где R' =м — постоянная
Так как v — то формула
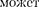 (209.1) быть переписана для ча- стот:
(209.1) быть переписана для ча- стот:
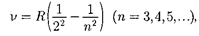 (209.2)
(209.2)
 где R=R'c 3.29 • 1015
где R=R'c 3.29 • 1015 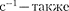 по- стоянная Ридберга.
по- стоянная Ридберга.
 Из выражений (209.1) и (209.2) вы- текает, что спектральные линии, отли- чающиеся различными значениями п, образуют группу или серию линий, на- зываемую серией Бальмера. Сувели- чением серии сближаются; зна- чение п = ооопределяет границу серии, которой со стороны больших частот
Из выражений (209.1) и (209.2) вы- текает, что спектральные линии, отли- чающиеся различными значениями п, образуют группу или серию линий, на- зываемую серией Бальмера. Сувели- чением серии сближаются; зна- чение п = ооопределяет границу серии, которой со стороны больших частот
примыкает сплошной спектр.
В дальнейшем (в начале XX в.) в спектре атома водорода было обнаруже- но еще несколько серий. В 

 (1854—1919) —
(1854—1919) —  уче-
уче-
 ный, в области спектроскопии.
ный, в области спектроскопии.
летовойобластиспектра находится се рия Лаймана:
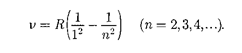
В инфракрасной области спектра
были также обнаружены:
|
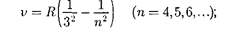 с
с 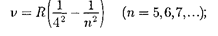 серия Брэкета
серия Брэкета
серия Пфунда
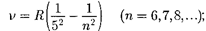
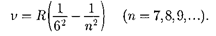 серия Хэмфри
серия Хэмфри
Все приведенные выше серии в спек- тре атома водорода могут быть описа- ны одной формулой, называемой обоб- щенной формулой 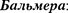
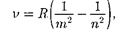 (209.3)
(209.3)
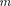 где имеет в каждой данной серии по- стоянное значение, т — 1,2,3,4,5,6 (оп- ределяет серию), п принимает целочис- ленные значения, начиная
где имеет в каждой данной серии по- стоянное значение, т — 1,2,3,4,5,6 (оп- ределяет серию), п принимает целочис- ленные значения, начиная 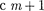 (оп- ределяет отдельныелинии этой серии). Исследование более сложных спек- тров — спектров паров щелочных метал- лов (например, Li, Na, К) — показало, что они представляются набором неза- кономерно расположенных линий. Рид-
(оп- ределяет отдельныелинии этой серии). Исследование более сложных спек- тров — спектров паров щелочных метал- лов (например, Li, Na, К) — показало, что они представляются набором неза- кономерно расположенных линий. Рид-  удалось разделить их на три се- рии, каждая из которых располагается подобно линиям бальмеровской серии. Приведенные выше сериальные фор- мулы подобраны эмпирически и долгое
удалось разделить их на три се- рии, каждая из которых располагается подобно линиям бальмеровской серии. Приведенные выше сериальные фор- мулы подобраны эмпирически и долгое
время не имели теоретического обосно- вания, хотя и  подтверждены экс- периментально с очень большой точно- стью. Приведенный выше вид сериаль- ных формул, удивительная повторяе- мость в них целых чисел, универсаль- ность постоянной Ридберга свидетель- ствуют о глубоком физическом смысле найденных закономерностей, вскрыть который в рамках классической физи- ки оказалось невозможным.
подтверждены экс- периментально с очень большой точно- стью. Приведенный выше вид сериаль- ных формул, удивительная повторяе- мость в них целых чисел, универсаль- ность постоянной Ридберга свидетель- ствуют о глубоком физическом смысле найденных закономерностей, вскрыть который в рамках классической физи- ки оказалось невозможным.
§  Постулаты Бора
Постулаты Бора
Первая попытка построить каче- ственно новую — квантовую — теорию атома была предпринята в 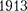 г. дат- ским физиком Нильсом Бором (1885 — 1962). Он поставил перед собой цель связать в единое целое эмпирические закономерности линейчатых спектров, ядерную модель атома Резерфорда и квантовый характер излучения и погло- щения света. В основу своей теории Бор положил два постулата.
г. дат- ским физиком Нильсом Бором (1885 — 1962). Он поставил перед собой цель связать в единое целое эмпирические закономерности линейчатых спектров, ядерную модель атома Резерфорда и квантовый характер излучения и погло- щения света. В основу своей теории Бор положил два постулата.
Первый постулат Бора (посту- латстационарныхсостояний): в ато- ме существуют стационарные (не изме- няющиеся со временем) состояния, в которых он не излучает энергии; эти со- стояния характеризуются определенны- ми дискретными значениями энергии.
Стационарным состояниям атома соответствуют стационарные орбиты, по которым движутся электроны. Дви- жение электронов по стационарным ор- битам не сопровождается излучением электромагнитных волн.
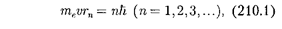 В стационарном состоянии атома электрон, двигаясь по круговой орби- те, должен иметь дискретные кванто- ванные значения момента импульса, удовлетворяющие условию
В стационарном состоянии атома электрон, двигаясь по круговой орби- те, должен иметь дискретные кванто- ванные значения момента импульса, удовлетворяющие условию
где — масса электрона; v — его ско- рость по 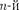 орбите радиуса
орбите радиуса 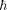 —
—
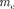
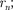
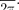 Второй постулат Бора (правило
Второй постулат Бора (правило
частот): при переходе электрона с од- ной стационарной орбиты на другую из- лучается (поглощается) один фотон с
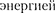
hv = 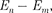 (210.2)
(210.2)
 равной разности энергий соответству- ющих стационарных состояний
равной разности энергий соответству- ющих стационарных состояний 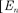
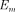 — соответственно энергии стацио- нарных состояний атома до и после из- лучения (поглощения)].
— соответственно энергии стацио- нарных состояний атома до и после из- лучения (поглощения)].
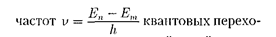 При
При 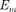 <
< 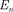 происходит излучение фотона (переход атома из состояния с большей энергией в состояние с мень- шей энергией, т. е. переход электрона с более удаленной от ядра орбиты на бо- лее близлежащую), при
происходит излучение фотона (переход атома из состояния с большей энергией в состояние с мень- шей энергией, т. е. переход электрона с более удаленной от ядра орбиты на бо- лее близлежащую), при 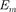 >
> 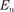 — его поглощение (переход атома в состояние с большей энергией, т. е. переход элект- рона на более удаленную от ядра ор- биту). Набор возможных дискретных
— его поглощение (переход атома в состояние с большей энергией, т. е. переход элект- рона на более удаленную от ядра ор- биту). Набор возможных дискретных
 дов и определяет спектр атома.
дов и определяет спектр атома.
§  Опыты Франка и Герца
Опыты Франка и Герца
Изучая методом задерживающего потенциала столкновения электронов с атомами газов (1913), Д.Франк и Г. Герц экспериментально доказали дис- кретность значений энергии атомов.
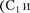 Принципиальная схема их установ- ки приведена на 295. Вакуумная трубка, заполненная парами ртути (дав- ление приблизительно равно 13 Па), со- держала катод (К), две сетки
Принципиальная схема их установ- ки приведена на 295. Вакуумная трубка, заполненная парами ртути (дав- ление приблизительно равно 13 Па), со- держала катод (К), две сетки 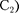 и анод (А). Электроны, эмиттируемые катодом, ускорялись разностью потен- циалов, приложенной между катодом и
и анод (А). Электроны, эмиттируемые катодом, ускорялись разностью потен- циалов, приложенной между катодом и
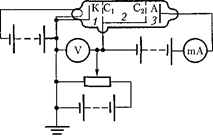
Рис. 295
сеткой 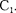 Между сеткой
Между сеткой 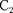 и анодом приложен небольшой (примерно 0,5 В) задерживающий потенциал.
и анодом приложен небольшой (примерно 0,5 В) задерживающий потенциал.
Электроны, ускоренные в области  попадают в область 2 между сетками, где испытывают соударения с атомами паров ртути. Электроны, которые после соударений имеют достаточную энер- гию для преодоления задерживающего потенциала в области 3, достигают ано- да. При неупругих соударениях элект- ронов с атомами ртути последние мо- гут возбуждаться. Согласно боровской теории, каждый из атомов ртути может получить лишь вполне определенную энергию, переходя при этом в одно из возбужденных состояний. Поэтому если в атомах действительно существу- ют стационарные состояния, то элект- роны, сталкиваясь с атомами ртути, должны терять энергию дискретно, оп- ределенными порциями, равными раз- ности энергий соответствующих стаци- онарных состояний атома.
попадают в область 2 между сетками, где испытывают соударения с атомами паров ртути. Электроны, которые после соударений имеют достаточную энер- гию для преодоления задерживающего потенциала в области 3, достигают ано- да. При неупругих соударениях элект- ронов с атомами ртути последние мо- гут возбуждаться. Согласно боровской теории, каждый из атомов ртути может получить лишь вполне определенную энергию, переходя при этом в одно из возбужденных состояний. Поэтому если в атомах действительно существу- ют стационарные состояния, то элект- роны, сталкиваясь с атомами ртути, должны терять энергию дискретно, оп- ределенными порциями, равными раз- ности энергий соответствующих стаци- онарных состояний атома.
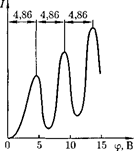 Рис. 296
Рис. 296
Из опыта следует (рис. 296), что при увеличении ускоряющего потенциала вплоть до 4,86 В анодный ток возраста- ет монотонно, его значение проходит через максимум 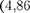 В), затем резко уменьшается и возрастает вновь. Даль- нейшие максимумы наблюдаются при
В), затем резко уменьшается и возрастает вновь. Даль- нейшие максимумы наблюдаются при 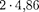 и
и 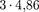 В.
В.
Ближайшим к основному, невозбуж- денному, состоянию атома ртути явля- ется возбужденное состояние, отстоя- щее от основного по шкале энергий на 4,86 эВ. Пока разность потенциалов между катодом и сеткой меньше 4,86 В, электроны, встречая на своем пути ато- мы ртути, испытывают с ними только упругие соударения.

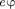 При 4,86 эВ энергия электрона становится достаточной, чтобы вызвать неупругий удар, при котором электрон отдает атому ртути всю кинетическую энергию, возбуждая переход одного из электронов атома из нормального энер- гетического состояния на возбужден- ный энергетический уровень. Электро- ны, потерявшие свою кинетическую энергию, уже не смогут преодолеть тор- мозящего поля и достигнуть анода. Этим и объясняется первое резкое па- дение анодного тока при = 4,86 эВ. При значениях энергии, кратных 4,86 эВ, электроны могут испытать с атомами ртути
При 4,86 эВ энергия электрона становится достаточной, чтобы вызвать неупругий удар, при котором электрон отдает атому ртути всю кинетическую энергию, возбуждая переход одного из электронов атома из нормального энер- гетического состояния на возбужден- ный энергетический уровень. Электро- ны, потерявшие свою кинетическую энергию, уже не смогут преодолеть тор- мозящего поля и достигнуть анода. Этим и объясняется первое резкое па- дение анодного тока при = 4,86 эВ. При значениях энергии, кратных 4,86 эВ, электроны могут испытать с атомами ртути 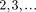 неупругих соударения, по- теряв при этом полностью свою энер- гию, и не достигнув анода, т.е. должно наблюдаться резкое падение анодного тока. Это действительно наблюдается на опыте (см. рис. 296).
неупругих соударения, по- теряв при этом полностью свою энер- гию, и не достигнув анода, т.е. должно наблюдаться резкое падение анодного тока. Это действительно наблюдается на опыте (см. рис. 296).
Таким образом, опыты Франка и Гер- ца показали, что электроны при столк- новении с атомами ртути передают ато- мам только определенные порции энер- гии, причем 4,86 эВ — наименьшая воз- можная порция энергии (наименьший квант энергии), которая может быть по- глощена атомом ртути в основном энер-
гетическом состоянии. Следовательно, идея Бора о существовании в атомах ста- ционарных состояний блестяще выдер- жала экспериментальную проверку.
Атомы ртути, получившие при соуда- рении с электронами энергию АЕ, пере- ходят в возбужденное состояние и дол- жны возвратиться в основное, излучая при этом, согласно второму постулату Бора [см. (210.2)], световой квант с час- тотой у = 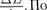 известному значению
известному значению
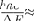
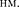 АЕ = 4,86 эВ можно вычислить длину волны излучения: X = 255
АЕ = 4,86 эВ можно вычислить длину волны излучения: X = 255

 Таким образом, если теория верна, то атомы ртути, бомбардируемые элек- тронами с энергией 4,86 эВ, должны яв- ляться источником ультрафиолетового излучения с X 255 нм. Опыт действи- тельно обнаруживает одну ультрафио- летовую линию с X 254 нм. Таким об- разом, опыты Франка и Герца экспери- ментально подтвердили не только пер- вый, но и второй постулат Бора. Эти опыты имели огромное значение в раз- витии атомной физики.
Таким образом, если теория верна, то атомы ртути, бомбардируемые элек- тронами с энергией 4,86 эВ, должны яв- ляться источником ультрафиолетового излучения с X 255 нм. Опыт действи- тельно обнаруживает одну ультрафио- летовую линию с X 254 нм. Таким об- разом, опыты Франка и Герца экспери- ментально подтвердили не только пер- вый, но и второй постулат Бора. Эти опыты имели огромное значение в раз- витии атомной физики.
§ 212. Спектр атома водорода по Бору
 Постулаты, выдвинутые Бором, по- зволили рассчитать спектр атома водо- рода и водородоподобных систем — систем, состоящих из ядра с Ze одного электрона (например, ионы
Постулаты, выдвинутые Бором, по- зволили рассчитать спектр атома водо- рода и водородоподобных систем — систем, состоящих из ядра с Ze одного электрона (например, ионы
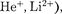 а также теоретически вычис- лить постоянную Ридберга.
а также теоретически вычис- лить постоянную Ридберга.
Следуя Бору, рассмотрим движение электрона в водородоподобной системе, ограничиваясь круговыми стационарны- ми орбитами. Решая совместно уравне-
т v2 Ze2

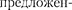
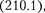 нис (208.1) —-— ,
нис (208.1) —-— ,
 |
ное Резерфордом, и уравнение
получим выражение для радиуса п-и стационарной орбиты:
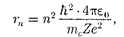 (212.1) где п= 1,2,3,... .
(212.1) где п= 1,2,3,... .
Из выражения 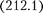 следует, что
следует, что
радиусы орбитрастут пропорциональ- но квадратам целых чисел.
Для атома водорода (Z = 1) радиус первой орбиты электрона при п = 1, на- зываемый первым воровским радиу- сом 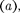 равен
равен
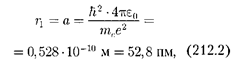
что соответствует расчетам на основа- нии кинетической теории газов.
Полная энергия электрона в водоро- доподобной системе складывается из
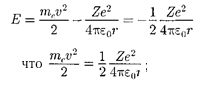
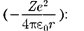

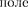 его кинетической энергии ( по- тенциальной энергии в электростати- ческом ядра (
его кинетической энергии ( по- тенциальной энергии в электростати- ческом ядра (
[учли, см. (208.1)].
Учитывая квантованные для радиуса n-й стационарной орбиты значения (212.1), получим, что энергия электро- на может принимать только следующие дозволенные дискретные значения:
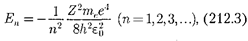 |
где знак «--»означает, что электрон на- ходится всвязанном состоянии.
Изформулы (212.3) следует, что энергетические состояния атома обра- зуют последовательность энергетиче- ских уровней, изменяющихся в зависи-

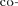 мости от значения Целое число п в выражении
мости от значения Целое число п в выражении 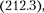 определяющее энер- гетические уровни атома, называется главным квантовым числом. Энерге- тическое состояние с п = 1 является основным (нормальным) состояни- ем; состояния с п > 1 являются воз- бужденными. Энергетический уро- вень, соответствующий основному стоянию атома, называется основным (нормальным) уровнем; все остальные уровни являются возбужденными.
определяющее энер- гетические уровни атома, называется главным квантовым числом. Энерге- тическое состояние с п = 1 является основным (нормальным) состояни- ем; состояния с п > 1 являются воз- бужденными. Энергетический уро- вень, соответствующий основному стоянию атома, называется основным (нормальным) уровнем; все остальные уровни являются возбужденными.
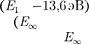 Придавая п различные целочислен- ные значения, получим для атома водо- рода
Придавая п различные целочислен- ные значения, получим для атома водо- рода 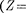 1), согласно формуле
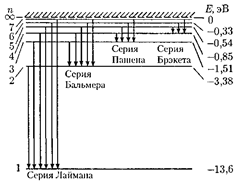
1), согласно формуле 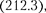 возможные уровни энергии, схемати- чески представленные на рис. 297. Энергия атома водорода с увеличени- ем п возрастает и энергетические уров- ни сближаются к границе, соответству- ющей значению п — ос. Атом водорода обладает, таким образом, минимальной энергией = при п= 1 и мак- симальной = 0) при п = оо. Следо- вательно, значение — 0 соответству- ет ионизации атома (отрыву от него электрона). Согласно второму постула- ту Бора [см. (210.2)], при переходе ато- ма водорода (Z = 1) из стационарного состояния п в стационарное состояние т с меньшей энергией испускается квант
возможные уровни энергии, схемати- чески представленные на рис. 297. Энергия атома водорода с увеличени- ем п возрастает и энергетические уров- ни сближаются к границе, соответству- ющей значению п — ос. Атом водорода обладает, таким образом, минимальной энергией = при п= 1 и мак- симальной = 0) при п = оо. Следо- вательно, значение — 0 соответству- ет ионизации атома (отрыву от него электрона). Согласно второму постула- ту Бора [см. (210.2)], при переходе ато- ма водорода (Z = 1) из стационарного состояния п в стационарное состояние т с меньшей энергией испускается квант
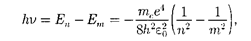 |
откуда частота излучения
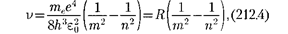
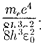 где R =
где R =
Воспользовавшись при вычислении R современными значениями универ- сальных постоянных, получим величи- ну, совпадающую с экспериментальным значением постоянной Ридберга в эм- 396
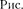 297
297
пирических формулах для атома водо- рода (см. § 209). Это совпадение убеди- тельно доказывает правильность полу- ченной Бором формулы (212.3) для энергетических уровней водородопо- добной системы.

 Подставляя, например, в формулу (212.4) т = 1 п = 2,3,4,..., получим группу линий, образующих серию Лай- мана (см. § 209) и соответствующих пе- реходам электронов с возбужденных уровней (?г = 2,3,4,...) на основной (т= 1). Аналогично, при подстановке т = 2,3,4,5,6 соответствующих им значений п получим серии Бальмера, Пашена, Брэкета, Пфунда и Хэмфри (часть из них схематически представле- на па рис. 297), описанные в § 209. Сле- довательно, по теории Бора, количе- ственно объяснившей спектр атома во- дорода, спектральные серии соответ- ствуют излучению, возникающему в результате перехода атома в данное со- стояние из возбужденных состояний, расположенных выше данного.
Подставляя, например, в формулу (212.4) т = 1 п = 2,3,4,..., получим группу линий, образующих серию Лай- мана (см. § 209) и соответствующих пе- реходам электронов с возбужденных уровней (?г = 2,3,4,...) на основной (т= 1). Аналогично, при подстановке т = 2,3,4,5,6 соответствующих им значений п получим серии Бальмера, Пашена, Брэкета, Пфунда и Хэмфри (часть из них схематически представле- на па рис. 297), описанные в § 209. Сле- довательно, по теории Бора, количе- ственно объяснившей спектр атома во- дорода, спектральные серии соответ- ствуют излучению, возникающему в результате перехода атома в данное со- стояние из возбужденных состояний, расположенных выше данного.
 Спектр поглощения атома водорода является линейчатым, но содержит при нормальных условиях только серию
Спектр поглощения атома водорода является линейчатым, но содержит при нормальных условиях только серию 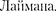 Он также объясняется теорией Бора. Так как свободные атомы водоро- да обычно находятся в
Он также объясняется теорией Бора. Так как свободные атомы водоро- да обычно находятся в
нии (стационарное состояние с наимень-
шей энергией при п = 1), то при сообще- нии атомам извне определенной энергии могут наблюдаться лишь переходы ато- мов из основного состояния в возбуж- денные (возникает серия Лаймана).
Теория Бора была крупным шагом в развитии атомной физики и явилась важным этапом в создании квантовой механики. Однако эта теория обладает внутренними противоречиями (с одной стороны, применяет законы классичес- кой физики, а с другой — основывается на квантовых постулатах).
В теории Бора рассмотрены спект- ры атома водорода и водородоподобных систем и вычислены частоты спект- ральных линий, однако эта теория не смогла объяснить интенсивности спек- тральных линий и ответить на вопрос: почему совершаются те или иные пере- ходы? Серьезным недостатком теории Бора была невозможность описания с ее помощью спектра атома гелия — од- ного из простейших атомов, непосред- ственно следующего за атомом водо- рода.
Контрольные вопросы
•  Почему атома оказалась несостоятельной?
Почему атома оказалась несостоятельной?
• Почему из различных серий спектральных линий атома водорода первой была изучена серия Бальмера?
• 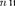
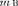 Какой смысл имеют числа обобщенной формуле Бальмера?
Какой смысл имеют числа обобщенной формуле Бальмера?
• Чему равна частота излучения атома водорода, соответствующая коротковолновой гра- нице серии Брэкета?
• Разъясните смысл постулатов Бора. Как с их 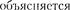 линейчатый спектр атома?
линейчатый спектр атома?
• На каких участках кривой рис. 296 наблюдаются упругие и пеупругие столкновения электронов с атомами?
• Какие основные выводы можно сделать на основании опытов Франка и Герца?
• Атом водорода находится в состоянии с п — 5. Сколько линий содержит его спектр излу- чения?
• 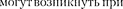 Пользуясь моделью Бора, укажите спектральные линии, которые переходе атома водорода из состояний с п = 3 и п — 4.
Пользуясь моделью Бора, укажите спектральные линии, которые переходе атома водорода из состояний с п = 3 и п — 4.
•  Нанесите шкалу длин волн три линии каждой из первых двух спектральных серий атома водорода.
Нанесите шкалу длин волн три линии каждой из первых двух спектральных серий атома водорода.
• Почему спектр поглощения атома водорода содержит только серию Лаймана?
• 
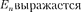 Покажите, что формулу (212.3) можно записать в виде =
Покажите, что формулу (212.3) можно записать в виде = 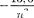 , где в электрон-вольтах.
, где в электрон-вольтах.
ЗАДАЧИ
27.1.  Определите максимальную и минимальную энергии фотона в ультрафиолетовой серии спектра атома водорода (серии Лаймана).
Определите максимальную и минимальную энергии фотона в ультрафиолетовой серии спектра атома водорода (серии Лаймана). 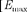 = 13,2 эВ,
= 13,2 эВ, 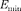 10,2 эВ)
10,2 эВ)
27.2. Определите длину волны, соответствующую границе серии Бальмера. [364 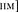
27.3. 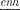 Используя теорию
Используя теорию 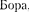 определите орбитальный магнитный момент электрона, движущегося по второй орбите атома водорода.
определите орбитальный магнитный момент электрона, движущегося по второй орбите атома водорода. 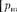 = = 1,8 • 10~23 А • м'2]
= = 1,8 • 10~23 А • м'2]
 21
21  Используя теорию
Используя теорию 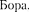 определите изменение орбитального механического мо- мента электрона при переходе его из возбужденного состояния (п = 2) в основное с испус- каниемфотона с длиной волны X = 1,212 • 10~7м. [AL = = 1,05 •
определите изменение орбитального механического мо- мента электрона при переходе его из возбужденного состояния (п = 2) в основное с испус- каниемфотона с длиной волны X = 1,212 • 10~7м. [AL = = 1,05 • 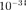 Дж • с]
Дж • с]
27.5. Определите потенциал ионизации атома водорода. [13,6 В]
27.6. 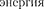 Основываясь на том, что ионизации атома водорода
Основываясь на том, что ионизации атома водорода 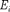 — 13,6 эВ, опреде- лите второй потенциал возбуждения этого атома. [12,1 В]
— 13,6 эВ, опреде- лите второй потенциал возбуждения этого атома. [12,1 В]
27.7. 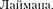 Основываясь на том, что энергия ионизации атома водорода
Основываясь на том, что энергия ионизации атома водорода 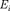 = 13,6 эВ, опреде- лите в электрон-вольтах этюргию фотона, соответствующую самой длинноволновой линии серии [10,2 эВ]
= 13,6 эВ, опреде- лите в электрон-вольтах этюргию фотона, соответствующую самой длинноволновой линии серии [10,2 эВ]
Глава 28
ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
§213. Корпускулярно-волновой дуализм свойств вещества
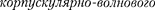 Французский ученый Луи де Бройль (1892 — 1987), осознавая существую- щую в природе симметрию и развивая представления о двойственной корпус- кулярно-волновой природе света, выд- винул в 1923 г. гипотезу об универсаль- ности дуализ-
Французский ученый Луи де Бройль (1892 — 1987), осознавая существую- щую в природе симметрию и развивая представления о двойственной корпус- кулярно-волновой природе света, выд- винул в 1923 г. гипотезу об универсаль- ности дуализ-
ма. Де Бройль утверждал, что не толь- ко фотоны, но и электроны и любые другие частицы материи наряду с кор- пускулярными обладают также волно- выми свойствами.

 Итак, согласно де Бройлю, с каждым микрообъектом связываются, с одной стороны, корпускулярные характерис- тики — энергия Е и импульс ас дру- гой — волновые характеристики — час- тота v длина волны X. Количествен- ные соотношения, связывающие кор- пускулярные и волновые свойства час- тиц, такие же, как для фотонов:
Итак, согласно де Бройлю, с каждым микрообъектом связываются, с одной стороны, корпускулярные характерис- тики — энергия Е и импульс ас дру- гой — волновые характеристики — час- тота v длина волны X. Количествен- ные соотношения, связывающие кор- пускулярные и волновые свойства час- тиц, такие же, как для фотонов:

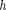 Е (213.1)
Е (213.1)
Смелость гипотезы де Бройля зак- лючалась именно в том, что соотноше- ние (213.1) постулировалось не только для фотонов, но и для других микроча- стиц (в частности, электронов). Таким образом, любой частице, обладающей
импульсом, сопоставляют
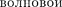 процесс, длина волны которого опреде- ляется по формуле де Бройля:
процесс, длина волны которого опреде- ляется по формуле де Бройля:
(213.2)
р
Вскоре гипотеза де Бройля была под- тверждена экспериментально. В 1927 г. американские физики К.Дэвиссон (1881-1958) и Л.Джермер (1896—
 1971) обнаружили, что пучок электро- нов, рассеивающийся от естественной дифракционной решетки — кристалла никеля, — дает отчетливую дифрак- ционную картину. Дифракционные максимумы соответствовали формуле Вульфа — Брэггов (182.1), брэгговская длина волны оказалась в точности рав- ной длине волны, вычисленной по фор- муле (213.2).
1971) обнаружили, что пучок электро- нов, рассеивающийся от естественной дифракционной решетки — кристалла никеля, — дает отчетливую дифрак- ционную картину. Дифракционные максимумы соответствовали формуле Вульфа — Брэггов (182.1), брэгговская длина волны оказалась в точности рав- ной длине волны, вычисленной по фор- муле (213.2).
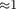 В дальнейшем формула де Бройля была подтверждена опытами П. С. Тар- таковского и Г. Томсона, наблюдавших дифракционную картину при прохож- дении пучка быстрых электронов (энер- гия
В дальнейшем формула де Бройля была подтверждена опытами П. С. Тар- таковского и Г. Томсона, наблюдавших дифракционную картину при прохож- дении пучка быстрых электронов (энер- гия 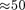 кэВ) через металлическую фольгу
кэВ) через металлическую фольгу 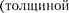
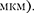
Так как дифракционная картина ис- следовалась для потока электронов, то необходимо было доказать, что волно- вые свойства присущи не только пото- ку большой совокупности электронов, но и каждому электрону в отдельности.
Это удалось экспериментально под- твердить в 1948 г. российскому физику  А.
А.  (1907- 1991).
(1907- 1991).  по-
по-
казал, что даже в случае столь слабо- го электронного пучка, когда каждый электрон проходит через прибор неза- висимо от других (промежуток време- ни между двумя электронами в 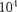 раз больше времени прохождения электро- ном прибора), возникающая при дли- тельной экспозиции дифракционная картина не отличается от дифракцион- ных картин, получаемых при короткой экспозиции для потоков электронов, в десятки миллионов раз более интенсив- ных. Следовательно, волновые свой- ства частиц не являются свойством их коллектива, а присущи каждой части- це в отдельности.
раз больше времени прохождения электро- ном прибора), возникающая при дли- тельной экспозиции дифракционная картина не отличается от дифракцион- ных картин, получаемых при короткой экспозиции для потоков электронов, в десятки миллионов раз более интенсив- ных. Следовательно, волновые свой- ства частиц не являются свойством их коллектива, а присущи каждой части- це в отдельности.
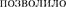 Впоследствии дифракционные яв- ления обнаружили также для нейтро- нов, протонов, атомных и молекуляр- ных пучков. Это окончательно послу- жило доказательством наличия волно- вых свойств микрочастиц и описывать движение микрочастиц в виде волнового процесса, характеризу- ющегося определенной длиной волны, рассчитываемой по формуле де Брой- ля
Впоследствии дифракционные яв- ления обнаружили также для нейтро- нов, протонов, атомных и молекуляр- ных пучков. Это окончательно послу- жило доказательством наличия волно- вых свойств микрочастиц и описывать движение микрочастиц в виде волнового процесса, характеризу- ющегося определенной длиной волны, рассчитываемой по формуле де Брой- ля 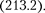 Открытие волновых свойств микрочастиц привело к появлению и развитию новых методов исследования структуры веществ, таких, как электро-
Открытие волновых свойств микрочастиц привело к появлению и развитию новых методов исследования структуры веществ, таких, как электро-
нография и нейтронография (см. § 182), а также к возникновению новой отрас- ли науки — электронной оптики (см.
§ 169).
 Экспериментальное доказательство наличия волновых свойств микрочас- тиц привело к выводу, что перед нами универсальное явление — общее свой- ство материи. Но тогда волновые свой- ства должны быть присущи и макроско- пическим телам. Почему же они не об- наружены экспериментально? Напри- мер, частице массой 1 г, со
Экспериментальное доказательство наличия волновых свойств микрочас- тиц привело к выводу, что перед нами универсальное явление — общее свой- ство материи. Но тогда волновые свой- ства должны быть присущи и макроско- пическим телам. Почему же они не об- наружены экспериментально? Напри- мер, частице массой 1 г, со
скоростью 1 м/с, соответствует волна де Бройля с X = 6,62 • 10~31м. Такая дли- на волны лежит за пределами доступ- ной наблюдению области (периодичес- ких структур с периодом d м не существует). Поэтому считается, что макроскопические тела проявляют только одну сторону 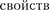 — корпускулярную и не проявляют вол- новую.
— корпускулярную и не проявляют вол- новую.
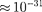
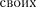 Представление о двойственной кор- пускулярно-волновой природе частиц вещества углубляется еще тем, что на частицы вещества переносится связь между полной энергией частицы и час- тотой:
Представление о двойственной кор- пускулярно-волновой природе частиц вещества углубляется еще тем, что на частицы вещества переносится связь между полной энергией частицы и час- тотой:
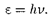 (213.3)
(213.3)
Это свидетельствует о том, что соот- ношение между энергией и частотой в формуле 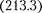 имеет характер универ- сального соотношения, справедливого как для фотонов, так и для любых дру- гих микрочастиц. Справедливость же соотношения
имеет характер универ- сального соотношения, справедливого как для фотонов, так и для любых дру- гих микрочастиц. Справедливость же соотношения 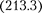 вытекает из согла- сия с опытом тех теоретических резуль- татов, которые получены с его помощью в квантовой механике, атомной и ядер- ной физике.
вытекает из согла- сия с опытом тех теоретических резуль- татов, которые получены с его помощью в квантовой механике, атомной и ядер- ной физике.
 Подтвержденная экспериментально гипотеза де Бройля о
Подтвержденная экспериментально гипотеза де Бройля о
 волновом дуализме свойств вещества коренным образом изменила представ- ления о свойствах микрообъектов. Всем микрообъектам присущи как корпуску- лярные, так и волновые свойства; в то же время любую из микрочастиц нельзя считать ни частицей, ни волной в клас- сическом понимании. Современная трактовка
волновом дуализме свойств вещества коренным образом изменила представ- ления о свойствах микрообъектов. Всем микрообъектам присущи как корпуску- лярные, так и волновые свойства; в то же время любую из микрочастиц нельзя считать ни частицей, ни волной в клас- сическом понимании. Современная трактовка
дуализма может быть выражена слова- ми академика В. А. Фока (1898 — 1974):
«Можно сказать, что для атомного объекта существует потенциальная воз- можность проявлять себя, в зависимо- сти от внешних условий, либо как вол-
на, либо как частица, либо промежу- точным образом. Именно в этой по- тенциальной возможности различных проявлений свойств, присущих микро- объекту, и состоит дуализм «волна — частица». Всякое иное, более букваль- ное, понимание этого дуализма в виде какой-нибудь модели неправильно.» (в сб.: Философские вопросы совре- менной физики. — М.: Изд-во АН СССР, 1959).
§ 214. Некоторые свойства волн де Бройля
 Рассмотрим свободно движущуюся со скоростью v частицу массой Вы- числим для нее фазовую и групповую скорости волн де Бройля. Фазовая ско- рость, согласно (154.8),
Рассмотрим свободно движущуюся со скоростью v частицу массой Вы- числим для нее фазовую и групповую скорости волн де Бройля. Фазовая ско- рость, согласно (154.8),
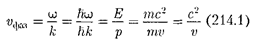 |
(Е = 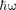 р —
р — 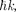 где к волно-
где к волно-

 X
X
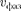

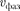 вое число). Так как с > v, то фазовая скорость волн де Бройля > (это возможно, так как не характеризу- ет ни скорости «сигнала», ни скорости перемещения энергии).
вое число). Так как с > v, то фазовая скорость волн де Бройля > (это возможно, так как не характеризу- ет ни скорости «сигнала», ни скорости перемещения энергии).
