Продольные и поперечные волны
Колебания, возбужденные в какой- либо точке среды (твердой, жидкой или газообразной), распространяются в ней с конечной скоростью, зависящей от свойств среды, передаваясь от одной точки среды к другой. Чем дальше расположена частица среды от источ- ника колебаний, тем позднее она нач-
нет колебаться. Иначе говоря, фазы колебаний частиц среды и источника тем больше отличаются друг от дру- га, чем больше это расстояние. При изучении распространения колебаний не учитывается дискретное (молеку- лярное) строение среды и среда рас- сматривается как сплошная, т.е. не- прерывно распределенная в простран- стве и обладающая упругими свой- ствами.
Процесс распространения колеба- ний в сплошной среде называется вол- новым процессом (или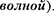 
При распространении волны частицы среды не движутся вместе с волной, а колеб- лются около своих положений равно- весия. Вместе с волной от частицы к частице среды передаются лишь состо- яние колебательного движения и его энергия. Поэтому основным свойством всех волн, независимо от их природы, является перенос энергии без переноса вещества.
Среди разнообразных волн, встреча- ющихся в природе и технике, выделя- ются следующие их типы: волны на по- верхности жидкости, упругие и элек- тромагнитныеволны. Упругими (или механическими) волнами называются механические возмущения, распростра- няющиеся в упругой среде. Упругие волны бывают продольные попереч- ные. В продольных волнах частицы среды колеблются в направлении рас- пространения волны, в поперечных — в плоскостях, перпендикулярных на- правлению распространения волны.
|
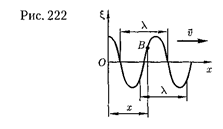
Упругая волна называется гармо- нической, если соответствующиеей ко- лебания частиц среды являются гармо- ническими. На рис. 222 представлена гармоническая поперечная волна, рас- пространяющаяся со скоростью v
оси х, т. е. приведена зависимость меж- ду смещением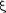 
частиц среды, участву- ющих в волновом процессе, и расстоя- нием х этих частиц (например, части- цы В) от источника колебаний О для какого-то фиксированного момента времени
Приведенный графикфункции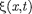 
напоминает график гармонического ко- лебания, однако они различны по суще- ству. График волны дает зависимость смещения всехчастиц среды от рассто- яния до источника колебаний в данный момент времени, а график колебаний — зависимость смещения данной частицы отвремени (см. рис. 202).
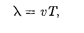Расстояние между ближайшими ча- стицами, колеблющимися в одинако- вой фазе, называется длиной волны X (рис. 222). Длина волны равна тому рас- стоянию, на которое распространяется определенная фаза колебания за пери- од, т.е.
газообразных телах. Поперечные волны могут возбуждаться в среде, в которой возникают упругие силы при деформа- ции сдвига, т.е. в твердых телах; в жид-
или, учитывая, что Т =
тота колебаний,
v = Xv.
1 , где у — час-
костях и газах возникают только про- дольныеволны, автвердыхтелах— как продольные, такипоперечные.
Если рассмотреть волновой процесс подробнее, то становится ясным, что ко- леблются не только частицы, располо- женные вдоль оси х, но и совокупность частиц, расположенных в некотором объеме, т. е. волна, распространяясь от источника колебаний, охватывает все новые и новые области пространства. Геометрическое место точек, до кото- рых доходят колебания к моменту вре- мени t, называется волновым фрон-
том. Геометрическое место точек, ко- леблющихся в одинаковой фазе, назы- вается волновойповерхностью, Волно- выхповерхностей можно провести бес- численное множество, а волновой фронт в каждый момент времени — один. Вол- новой фронт также волновой поверхностью. Волновые поверхности могут быть любой формы, а в простей- шем случае они представляют собой со- вокупность плоскостей, параллельных друг другу, или совокупность концент- рических сфер. Соответственно волна называется плоской или сферической.
§ 154. Уравнение бегущей волны.