И его решение. Автоколебания
Рассмотрим свободные затухаю- щие колебания — колебания, амплиту- ды которых из-за потерь энергии реаль- ной колебательной системой с течени- ем времени уменьшаются. Простейшим механизмом уменьшения энергии коле- баний является ее превращение в теп- лоту вследствие трения в механических
 системах, а также оми- ческих потерь и излучения электромаг-
системах, а также оми- ческих потерь и излучения электромаг-
нитнои энергии в электрических коле- бательных системах.
Закон затухания 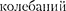 опреде- ляется свойствами колебательных сис- тем. Обычно рассматривают линейные системы — идеализированные реаль- ные системы, в которых параметры, определяющие физические свойства
опреде- ляется свойствами колебательных сис- тем. Обычно рассматривают линейные системы — идеализированные реаль- ные системы, в которых параметры, определяющие физические свойства
+ 0. (146.3)
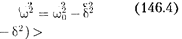
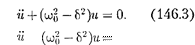 Решение уравнения (146.3) зависит от знака коэффициента перед искомой величиной. Рассмотрим случай, когда этот коэффициент положителен:
Решение уравнения (146.3) зависит от знака коэффициента перед искомой величиной. Рассмотрим случай, когда этот коэффициент положителен:
(146.4)
системы, в ходе процесса не изменяют-
[если (из
0, то такое обозначе-
ся. Линейными системами являются, например, пружинный маятник при ма- лых растяжениях пружины (когда спра- ведлив закон Гука), колебательный контур, индуктивность, емкость и со- противление которого не зависят ни от тока в контуре, ни от напряжения.
Различные по своей природе линей- ные системы описываются идентичны- ми линейными дифференциальными уравнениями, что позволяет подходить к изучению колебаний различной фи- зической природы с единой точки зре- ния, а также проводить их моделирова- ние, в том числе и на ЭВМ.
Дифференциальное уравнение свободных затухающих колебаний линейной системы задается в виде
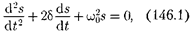

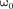 где s —колеблющаяся величина, опи- сывающая тот или иной физический процесс; б const — коэффициент за- тухания, —циклическая частота свободных незатухающих колебаний той же колебательной системы, т.е. при б — 0(при отсутствии потерь энергии) называется собственной частотой колебательной системы.
где s —колеблющаяся величина, опи- сывающая тот или иной физический процесс; б const — коэффициент за- тухания, —циклическая частота свободных незатухающих колебаний той же колебательной системы, т.е. при б — 0(при отсутствии потерь энергии) называется собственной частотой колебательной системы.
Решение уравнения 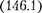 рассмот- рим в виде
рассмот- рим в виде
ние мы вправе сделать]. Тогда получим


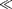 уравнение типа (142.1) +
уравнение типа (142.1) + 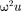 0, ре- шением которого является функция и=
0, ре- шением которого является функция и= 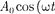 +
+ 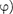 [см. (140.1)]. Таким образом, решение уравнения (146.1) в случае малых затуханий
[см. (140.1)]. Таким образом, решение уравнения (146.1) в случае малых затуханий 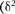
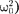
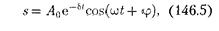 + (146.5)
+ (146.5)
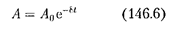 где
где
— амплитуда затухающих колеба-
ний; 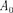 — начальная амплитуда.
— начальная амплитуда.
 Зависимость (146.5) показана па рис.
Зависимость (146.5) показана па рис.  сплошной линией, а зависи- мость (146.6) — штриховыми
сплошной линией, а зависи- мость (146.6) — штриховыми
Промежуток времени т = -, в течение
которого амплитуда затухающих коле- баний уменьшается в е раз, называется временем релаксации.
 Затухание нарушает периодичность колебаний, поэтому затухающие коле- бания не являются периодическими и, строго говоря, к ним неприменимо по- нятие периода или частоты. Однако если затухание мало, то можно услов- но пользоваться понятием периода как промежутка времени между двумя пос-
Затухание нарушает периодичность колебаний, поэтому затухающие коле- бания не являются периодическими и, строго говоря, к ним неприменимо по- нятие периода или частоты. Однако если затухание мало, то можно услов- но пользоваться понятием периода как промежутка времени между двумя пос-
где
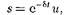 (146.2)
(146.2)
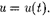
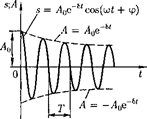 После нахождения первой и второй
После нахождения первой и второй
производных выражения (146.2) и под- становки их в (146.1) получим
ледующими максимумами (или мини- мумами) колеблющейся физической величины (см. рис. 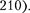 Тогда период затухающих колебаний с учетом фор- мулы (146.4) равен
Тогда период затухающих колебаний с учетом фор- мулы (146.4) равен
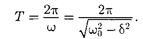 |
Если A(t) и 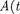 + T) — амплитуды двух последовательных колебаний, со- ответствующих моментам времени, от- личающимся на период, то отношение
+ T) — амплитуды двух последовательных колебаний, со- ответствующих моментам времени, от- личающимся на период, то отношение
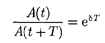
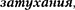 называется декрементом
называется декрементом
а его логарифм
ских (в качестве примера рассмотрим пружинный маятник) и электромагнит- ных (в качестве примера рассмотрим электрический колебательный контур).
1. Свободные затухающие колеба- ния пружинного маятника. Для пру- жинного маятника (см. § 142) массой т, совершающего малые колебания под действием упругой силы F= 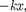 сила трения пропорциональна скорости, т. е.
сила трения пропорциональна скорости, т. е.
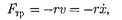 |
где г 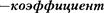 сопротивления; знак «-» указывает на противополож- ные направления силы трения и скоро- сти.
сопротивления; знак «-» указывает на противополож- ные направления силы трения и скоро- сти.
При данных условиях закон движе- ния маятника будет иметь вид
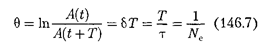
— логарифмическим декрементом затухания; 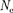 — число колебаний, со- вершаемых за время уменьшения амп- литуды в е раз. Логарифмический дек- ремент затухания — постоянная вели- чина для данной колебательной систе- мы.
— число колебаний, со- вершаемых за время уменьшения амп- литуды в е раз. Логарифмический дек- ремент затухания — постоянная вели- чина для данной колебательной систе- мы.
Для характеристики колебательной системы пользуются понятием доб- ротности Q, которая при малых зна- чениях логарифмического декремента
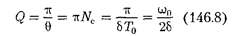 |
(так как затухание мало (б2 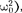 то
то
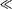 Т принято равным
Т принято равным 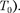
Из формулы (146.8) следует, что добротность пропорциональна числу колебаний 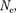 совершаемых системой за время релаксации.
совершаемых системой за время релаксации.
Выводы, полученные для свободных затухающих колебаний линейных сис- тем, применимы для колебаний различ- ной физической природы — механиче-
(146.9)
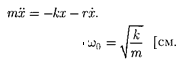 Используя формулу
Используя формулу
(142.2)] и принимая, что коэффициент затухания

получим идентичное уравнению (146.1) дифференциальное уравнение затухаю- щих колебаний маятника:
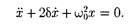
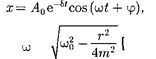 Извыражений (146.1) и(146.5) вы- текает, что колебания маятника подчи- няются закону
Извыражений (146.1) и(146.5) вы- текает, что колебания маятника подчи- няются закону
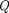
 гдечастота = [см. (146.4)]. Добротность пружинного маятника, согласно (146.8) и (146.10),
гдечастота = [см. (146.4)]. Добротность пружинного маятника, согласно (146.8) и (146.10), 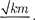
2. Свободные затухающие колеба- ния в электрическом колебательном контуре.Дифференциальное уравне- ние свободных затухающих колебаний
 заряда в контуре (при R 0) имеет вид [см. (143.2)]
заряда в контуре (при R 0) имеет вид [см. (143.2)]
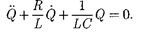 |
Учитывая выражение (143.4) и прини- мая коэффициент затухания
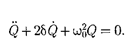 Извыражений (146.1) и (146.5) выте- кает, что колебания заряда совершают- ся позакону
Извыражений (146.1) и (146.5) выте- кает, что колебания заряда совершают- ся позакону
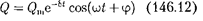
с частотой, согласно (146.4),
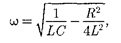
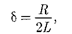
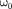 (146.11) (146.13)
(146.11) (146.13)
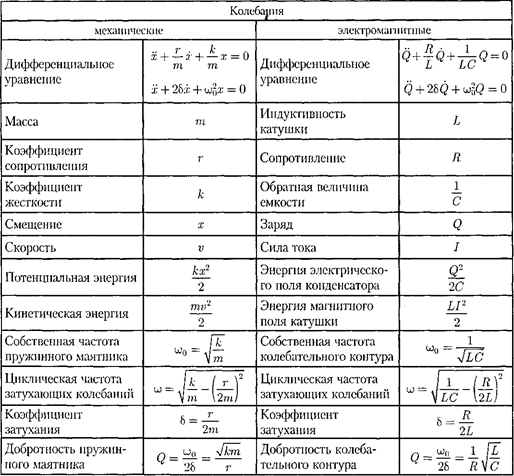
дифференциальное уравнение (143.2) можно записать в идентичном уравне- нию (146.1) виде
меньшей собственной частоты конту- ра [см. (143.4)]. При R = 0 формула (146.13) переходит в (143.4).
 |
 Т а б л ц а 7
Т а б л ц а 7Логарифмический декремент зату- хания определяется формулой (146.7), а добротность колебательного контура [см. 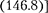
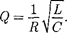 (146.14)
(146.14)
В табл. 7 произведено сопоставление затухающих колебаний пружинного маятника и колебаний в электрическом колебательном контуре.
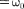
 В заключение отметим, что при уве- личении коэффициента затухания 6 пе- риод затухающих колебаний растет и при 8 обращается в бесконечность, т.е. движение перестает быть периоди- ческим. В этом случае колеблющаяся величина асимптотически приближает- ся к нулю, когда t со. Данный про- цесс будет апериодическим, а не коле- бательным.
В заключение отметим, что при уве- личении коэффициента затухания 6 пе- риод затухающих колебаний растет и при 8 обращается в бесконечность, т.е. движение перестает быть периоди- ческим. В этом случае колеблющаяся величина асимптотически приближает- ся к нулю, когда t со. Данный про- цесс будет апериодическим, а не коле- бательным.
Огромный интерес для техники пред- ставляет возможность поддерживать колебания незатухающими. Для этого необходимо восполнять потери энергии реальной колебательной системы. Осо- бенно важны и широко применимы так называемые автоколебания — незату- хающие колебания, поддерживаемые в
 системе за счет посто- янного внешнего источника энергии, причем свойства этих колебаний опре- деляются самой системой.
системе за счет посто- янного внешнего источника энергии, причем свойства этих колебаний опре- деляются самой системой.
Автоколебания принципиально от- личаются от свободных незатухающих колебаний, происходящих без последу- ющих внешних воздействий, а также от вынужденных колебаний (см. § 147), происходящих под действием периоди- ческой силы. Автоколебательная систе- ма сама управляет внешними воздей- ствиями, обеспечивая согласованность поступления энергии определенными порциями в нужный момент времени (в такт с ее колебаниями).
Примером автоколебательной сис- темы могут служить часы. Храповой механизм подталкивает маятник в такт с колебаниями. Энергия, переда- ваемая при этом маятнику, берется либо за счет раскручивающейся пру- жины, либо за счет опускающегося груза. Колебания воздуха в духовых инструментах и органных трубах так- же возникают вследствие автоколе- баний, поддерживаемых воздушной струей.
 системами яв- ляются также двигатели внутреннего сгорания, паровые турбины, ламповые генераторы и т.д.
системами яв- ляются также двигатели внутреннего сгорания, паровые турбины, ламповые генераторы и т.д.
§ 147. Дифференциальное уравнение вынужденных колебаний (механических и электромагнитных)
И его решение
Чтобы в реальной колебательной системе получить незатухающие коле- бания, надо компенсировать потери энергии. Такая компенсация возможна с помощью какого-либо периодически действующего фактора 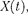 изменяю- щего по гармоническому закону:
изменяю- щего по гармоническому закону:
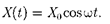
Если рассматривать механические колебания, то роль X(t) играет внешняя вынуждающая сила
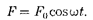 (147.1)
(147.1)
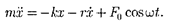 С учетом (147.1) закон движения для пружинного маятника
С учетом (147.1) закон движения для пружинного маятника 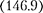 запи- шется в виде
запи- шется в виде
Используя (142.2) и (146.10), при- дем к уравнению
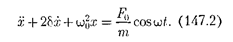
Если рассматривать электрический колебательный контур, то роль 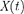 иг- рает подводимая к контуру внешняя периодически изменяющаяся по гармо- ническому закону ЭДС или
иг- рает подводимая к контуру внешняя периодически изменяющаяся по гармо- ническому закону ЭДС или 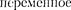 напряжение
напряжение
пой форме (см. § 140). Заменим правую часть уравнения (147.5) на комплекс- ную величину 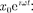
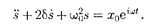 (147.6)
(147.6)
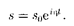 Частное решение этого уравнения бу- дем искать в виде
Частное решение этого уравнения бу- дем искать в виде
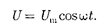
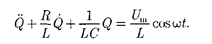
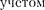 Тогда уравнение (143.2) с (147.3) можно записать в виде
Тогда уравнение (143.2) с (147.3) можно записать в виде
(147.3)
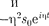
 Подставляя выражение для s его про- изводных
Подставляя выражение для s его про- изводных  =
= 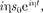 — ) в уравнение (147.6), получим
— ) в уравнение (147.6), получим

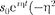 +
+ 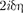 +
+ 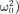 = (147.7)
= (147.7)
Так как это равенство должно быть
Используя (143.4) и (146.11), при- дем к уравнению
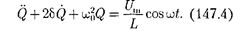 |
Колебания, возникающие под дей- ствием внешней периодически изменя- ющейся силы или внешней периодиче- ски изменяющейся ЭДС, называются
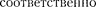 вынужденными меха- ническими и вынужденными элект- ромагнитными колебаниями.
вынужденными меха- ническими и вынужденными элект- ромагнитными колебаниями.
Уравнения (147.2) и (147.4) можно свести к линейному неоднородному дифференциальному уравнению
справедливым для всех моментов вре- мени, то время t из него должно исклю- чаться. Отсюда следует, что т| = со. Учи- тывая это, из уравнения (147.7) найдем величину и умножим ее числитель и знаменатель на 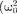
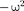 —
— 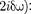

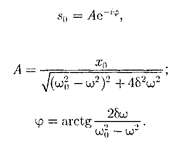
 Это комплексное число удобно пред- ставить в экспоненциальной форме:
Это комплексное число удобно пред- ставить в экспоненциальной форме:
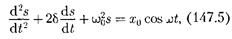
применяя впоследствии его решение для вынужденных колебаний конкрет- ной физической природы 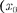 в случае
в случае
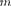
|
где
(147.8)
(147.9)
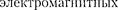 случае
случае
U ).
Следовательно, решение уравнения (147.6) в комплексной форме примет

 Решение уравнения (147.5) равно сумме общего решения (146.5) одно- родного уравнения (146.1) частного решения неоднородного уравнения. Частное решение найдем в комплекс-
Решение уравнения (147.5) равно сумме общего решения (146.5) одно- родного уравнения (146.1) частного решения неоднородного уравнения. Частное решение найдем в комплекс-
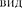
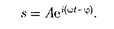 Его вещественная часть, являющая- ся решением уравнения (147.5), равна
Его вещественная часть, являющая- ся решением уравнения (147.5), равна
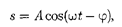 (147.10)
(147.10)
где 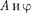 задаются соответственно фор- мулами (147.8) и (147.9).
задаются соответственно фор- мулами (147.8) и (147.9).
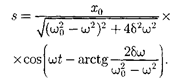 Таким образом, частное решение неоднородного уравнения (147.5) име- ет вид
Таким образом, частное решение неоднородного уравнения (147.5) име- ет вид
(147.11)
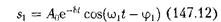 Решение уравнения (147.5) равно сумме общего решения однородного уравнения
Решение уравнения (147.5) равно сумме общего решения однородного уравнения
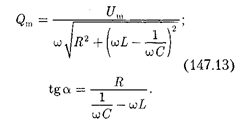
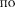 Дифференцируя
Дифференцируя 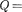
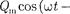 a) t, найдем силу тока в контуре при
a) t, найдем силу тока в контуре при
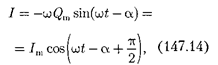 установившихся колебаниях:
установившихся колебаниях:
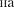

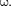 [см. (146.5)] и частного решения
[см. (146.5)] и частного решения 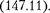 Слагаемое (147.12) играет существен- ную роль только в начальной стадии процесса (при установлении колеба- ний) до тех пор, пока амплитуда вынуж- денных колебаний не достигнет значе- ния, определяемого равенством (147.8). Графически вынужденные колебания представлены рис.
Слагаемое (147.12) играет существен- ную роль только в начальной стадии процесса (при установлении колеба- ний) до тех пор, пока амплитуда вынуж- денных колебаний не достигнет значе- ния, определяемого равенством (147.8). Графически вынужденные колебания представлены рис. 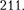 Следователь- но, в установившемся режиме вынуж- денные колебания происходят с часто- той и являются гармоническими; ам- плитуда и фаза колебаний, определяе- мые выражениями (147.8) и (147.9), также зависят от
Следователь- но, в установившемся режиме вынуж- денные колебания происходят с часто- той и являются гармоническими; ам- плитуда и фаза колебаний, определяе- мые выражениями (147.8) и (147.9), также зависят от
Запишем формулы (147.10), (147.8) и (147.9) для электромагнитных коле- баний, учитывая, что [см.
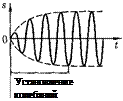 Рис.211
Рис.211
где
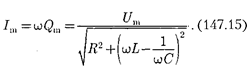
Выражение (147.14) может быть за- писано ввиде
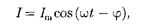

 где —сдвиг пофазе между
где —сдвиг пофазе между
током и приложенным напряжением [см. (147.3)].
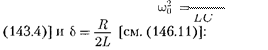 Всоответствии с выражением (147.13)
Всоответствии с выражением (147.13)
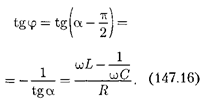
Изформулы (147.16) вытекает, что ток отстает пофазе от напряжения
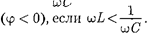
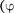 >0), если
>0), если 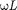 > ——,и опережает на- пряжение
> ——,и опережает на- пряжение
Формулы (147.15) PI (147.16) мож- но также получить с помощью вектор- ной диаграммы (см. § 149).
§ 148. Амплитуда и фаза вынужденных колебаний (механических
И электромагнитных).
Резонанс
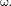 Рассмотрим зависимость амплиту- ды А вынужденных колебаний от час- тоты Механические и электромаг- нитные колебания будем рассматривать одновременно, называя колеблющуюся величину либо смещением (х) колеблю- щегося тела из положения равновесия, либо зарядом (Q) конденсатора.
Рассмотрим зависимость амплиту- ды А вынужденных колебаний от час- тоты Механические и электромаг- нитные колебания будем рассматривать одновременно, называя колеблющуюся величину либо смещением (х) колеблю- щегося тела из положения равновесия, либо зарядом (Q) конденсатора.
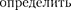
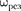
 Из формулы (147.8) следует, что амплитуда А смещения (заряда) имеет максимум. Чтобы резонан- сную частоту — частоту, при ко- торой амплитуда А смещения (заряда) достигает максимума, — нужно найти максимум функции (147.8), или, что то же самое, минимум подкоренного вы- ражения. Продифференцировав подко- ренное выражение и приравняв его нулю, получим условие, определяющее
Из формулы (147.8) следует, что амплитуда А смещения (заряда) имеет максимум. Чтобы резонан- сную частоту — частоту, при ко- торой амплитуда А смещения (заряда) достигает максимума, — нужно найти максимум функции (147.8), или, что то же самое, минимум подкоренного вы- ражения. Продифференцировав подко- ренное выражение и приравняв его нулю, получим условие, определяющее
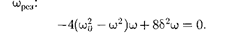
 Эторавенствовыполняется
Эторавенствовыполняется 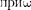 О,
О,
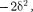
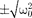 у которых только лишь по- ложительное значение имеет физиче- ский смысл. Следовательно, резонанс- ная частота
у которых только лишь по- ложительное значение имеет физиче- ский смысл. Следовательно, резонанс- ная частота
или близкой собственной частоте коле- бательной системы, называется резо- нансом (соответственно механи- ческим или электрическим). При б2 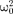 значение практически со- впадает с собственной частотой коле- бательной системы. Подставляя (148.1) в формулу (147.8), получим
значение практически со- впадает с собственной частотой коле- бательной системы. Подставляя (148.1) в формулу (147.8), получим
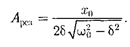
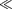
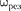
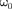 (148.2)
(148.2)
 На рис. 212 приведены
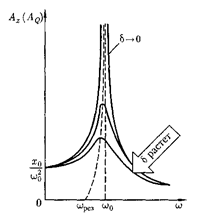
На рис. 212 приведены
 амплитуды вынужденных колебаний от частоты при различных значениях 8. Из (148.1) и (148.2) вытекает, что чем меньше 8, тем выше и правее лежит мак- симум данной кривой. Если со 0, то все кривые [см. также (147.8)] достига- ют одного и того же, отличного от нуля, предельного значения которое
амплитуды вынужденных колебаний от частоты при различных значениях 8. Из (148.1) и (148.2) вытекает, что чем меньше 8, тем выше и правее лежит мак- симум данной кривой. Если со 0, то все кривые [см. также (147.8)] достига- ют одного и того же, отличного от нуля, предельного значения которое
зывают статическим отклонением.
 В случае механических колебаний
В случае механических колебаний
— в случае электромагнитных —

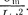 Если —> 0, то все кривые асимп- тотически стремятся к нулю. Приведен- ная совокупность кривых называется резонансными кривыми.
Если —> 0, то все кривые асимп- тотически стремятся к нулю. Приведен- ная совокупность кривых называется резонансными кривыми.
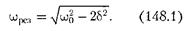
 Явление резкого возрастания амп- литуды вынужденных колебаний при приближении частоты вынуждающей силы (частоты вынуждающего пере-
Явление резкого возрастания амп- литуды вынужденных колебаний при приближении частоты вынуждающей силы (частоты вынуждающего пере-
менного напряжения) к частоте, равной Рис.212
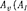
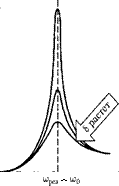 Рис.213
Рис.213
максимальна при = и равна 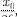
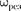
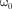 т.е. чем больше коэффициент затуха- ния б, тем ниже максимум резонансной кривой. Используя формулы (142.2), (146.10) и (143.4), (146.11), получим,
т.е. чем больше коэффициент затуха- ния б, тем ниже максимум резонансной кривой. Используя формулы (142.2), (146.10) и (143.4), (146.11), получим,
что амплитуда скорости при механиче- ском резонансе равна
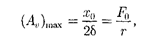
аамплитуда тока при электрическом резонансе
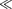 Из формулы (148.2) вытекает, что при малом затухании
Из формулы (148.2) вытекает, что при малом затухании 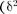
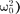 резо- нансная амплитуда смещения (заряда)
резо- нансная амплитуда смещения (заряда)
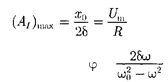
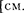 Из выражения tg =
Из выражения tg =
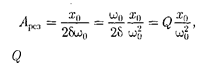

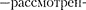 где — добротность колебательной системы [см. (146.8)];
где — добротность колебательной системы [см. (146.8)];
ное выше статическое отклонение.
Отсюда следует, что добротность 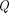 характеризует резонансные свойства колебательной системы: чем больше Q,
характеризует резонансные свойства колебательной системы: чем больше Q,

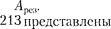 больше
больше
На рис. резонанс-
ные кривые для амплитуды скорости (тока). Амплитуда скорости (тока)
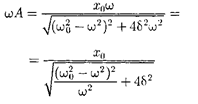
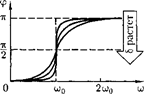 Рис.214
Рис.214
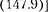 следует, что если затухание в системе отсутствует (8 = 0), то только в этом случае колебания и вынуждаю- щая сила (приложенное переменное на- пряжение) имеют одинаковые фазы; во всех других случаях 0.
следует, что если затухание в системе отсутствует (8 = 0), то только в этом случае колебания и вынуждаю- щая сила (приложенное переменное на- пряжение) имеют одинаковые фазы; во всех других случаях 0.





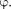




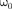

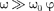
 Зависимость от при разных ко- эффициентах 8 графически представле- на на рис.
Зависимость от при разных ко- эффициентах 8 графически представле- на на рис.  из которого следует, что при изменении изменяется и сдвиг фаз Из формулы (147.9) вытекает, что при — 0 0, а при = не зависимо от значения коэффициента затухания Ф = —, т.е. сила (напряже- ние) опережает по фазе колебания на —. При дальнейшем увеличении сдвиг фаз возрастает и при е. фаза колебаний почти противополож- на фазе внешней силы (переменного на- пряжения). Семейство кривых, изобра- женных нарис. 214, называется фазо- выми резонансными кривыми.
из которого следует, что при изменении изменяется и сдвиг фаз Из формулы (147.9) вытекает, что при — 0 0, а при = не зависимо от значения коэффициента затухания Ф = —, т.е. сила (напряже- ние) опережает по фазе колебания на —. При дальнейшем увеличении сдвиг фаз возрастает и при е. фаза колебаний почти противополож- на фазе внешней силы (переменного на- пряжения). Семейство кривых, изобра- женных нарис. 214, называется фазо- выми резонансными кривыми.
Явления резонанса могут быть как вредными, так и полезными. Например, при конструировании машин и различ- ного рода сооружений необходимо, что- бы собственная частота их колебаний
 совпадала с возможных внешних воздействий, в противном случае возникнут вибрации, которые могут вызвать серьезные разрушения. С другой стороны, наличие резонанса позволяет обнаружить даже очень сла- бые колебания, если их частота совпа- дает с частотой собственных колебаний прибора. Так, радиотехника, приклад- ная акустика, электротехника исполь- зуют явление резонанса.
совпадала с возможных внешних воздействий, в противном случае возникнут вибрации, которые могут вызвать серьезные разрушения. С другой стороны, наличие резонанса позволяет обнаружить даже очень сла- бые колебания, если их частота совпа- дает с частотой собственных колебаний прибора. Так, радиотехника, приклад- ная акустика, электротехника исполь- зуют явление резонанса.
Рис.215
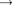
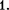 Переменный ток, текущий через резистор сопротивлениемR (L О,
Переменный ток, текущий через резистор сопротивлениемR (L О,
 0) (рис. 215,
0) (рис. 215,  При выполнении условия квазистационарности ток через резистор определяется законом Ома:
При выполнении условия квазистационарности ток через резистор определяется законом Ома:
§149.Переменныйток

 вынужденные элек- тромагнитные колебания (см. § 147) можно рассматривать как протекание в цепи, содержащей резистор, катушку индуктивности и конденсатор перемен- ного тока. Переменный ток можно считать квазистационарным, е. для него мгновенные силы тока во всех сечениях цепи практически одина- ковы, так как их изменения происходят достаточно медленно, а электромагнит- ные возмущения распространяются по цепи со скоростью, равной скорости света.
вынужденные элек- тромагнитные колебания (см. § 147) можно рассматривать как протекание в цепи, содержащей резистор, катушку индуктивности и конденсатор перемен- ного тока. Переменный ток можно считать квазистационарным, е. для него мгновенные силы тока во всех сечениях цепи практически одина- ковы, так как их изменения происходят достаточно медленно, а электромагнит- ные возмущения распространяются по цепи со скоростью, равной скорости света.
Для мгновенных значений квазиста- ционарных токов выполняются закон Ома и вытекающие из пего правила Кирхгофа, которые будут использова- ны применительно к переменным то- кам (эти законы уже использовались при рассмотрении электромагнитных колебаний).
 Рассмотрим последовательно про- цессы, происходящие участке цепи, содержащем резистор, катушку индук- тивности и конденсатор, к концам ко- торого приложено переменное напря- жение
Рассмотрим последовательно про- цессы, происходящие участке цепи, содержащем резистор, катушку индук- тивности и конденсатор, к концам ко- торого приложено переменное напря- жение
где

 Для наглядного изображения соот- ношений между переменными токами и напряжениями воспользуемся
Для наглядного изображения соот- ношений между переменными токами и напряжениями воспользуемся
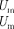 дом векторных диаграмм.
дом векторных диаграмм. 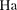 рис.
рис. 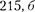 дана векторная диаграмма амплитуд- ных значенийтока
дана векторная диаграмма амплитуд- ных значенийтока 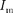 и напряжения
и напряжения
на резисторе (сдвиг фаз между 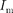 и равен нулю).
и равен нулю).
 2. Переменный ток, текущий через катушку индуктивностьюL (R 0,
2. Переменный ток, текущий через катушку индуктивностьюL (R 0,

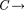 0) (рис. 216, а). Если в цепи прило- жено переменное напряжение
0) (рис. 216, а). Если в цепи прило- жено переменное напряжение 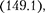 то в ней потечет переменный ток, в резуль- тате чего возникнет
то в ней потечет переменный ток, в резуль- тате чего возникнет 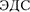 самоиндук- ции [см. (126.3)]
самоиндук- ции [см. (126.3)] 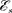 —L— . Тогда за-
—L— . Тогда за-
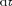
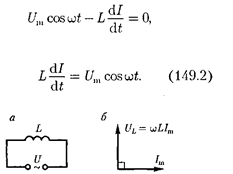 кон Ома [см. (100.3)] для рассматрива- емого участка цепи имеет вид
кон Ома [см. (100.3)] для рассматрива- емого участка цепи имеет вид
откуда
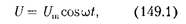
где 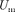 — амплитуда напряжения.
— амплитуда напряжения.
Рис.216
Так как внешнее напряжение приложе- но к катушке индуктивности, то
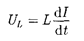 (149.3)
(149.3)
есть падение напряжения на катушке. Из уравнения (149.2) следует, что
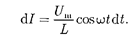
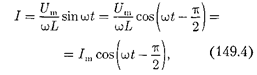 После интегрирования, учитывая, что постоянная интегрирования равна нулю (так как отсутствует постоянная состав- ляющая тока), получим
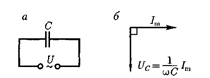
После интегрирования, учитывая, что постоянная интегрирования равна нулю (так как отсутствует постоянная состав- ляющая тока), получим
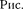 217
217
 L —> 0)
L —> 0) 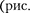 217,
217, 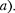 Если переменное напряжение (149.1) приложено к кон- денсатору, то он все время перезаряжа- ется, и в цепи течет переменный ток. Так как все внешнее напряжение при- ложено к конденсатору, а сопротивле- нием подводящих проводов можно пре- небречь,
Если переменное напряжение (149.1) приложено к кон- денсатору, то он все время перезаряжа- ется, и в цепи течет переменный ток. Так как все внешнее напряжение при- ложено к конденсатору, а сопротивле- нием подводящих проводов можно пре- небречь,
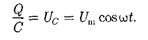 |
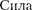 тока
тока
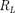 где
где 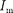 = Величина
= Величина
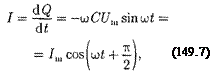 (149.5)
(149.5)
 называется реактивным индуктив- ным сопротивлением (или индуктив- ным сопротивлением). Из выражения (149.5) вытекает, что для постоянного тока
называется реактивным индуктив- ным сопротивлением (или индуктив- ным сопротивлением). Из выражения (149.5) вытекает, что для постоянного тока 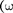 — 0) катушка индуктивности не имеет сопротивления. Подстановка зна- чения
— 0) катушка индуктивности не имеет сопротивления. Подстановка зна- чения 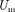 =
= 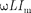 в выражение (149.2) с учетом (149.3) приводит к следующе- му значению падения напряжения на катушке индуктивности:
в выражение (149.2) с учетом (149.3) приводит к следующе- му значению падения напряжения на катушке индуктивности:
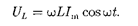 (149.6)
(149.6)
Сравнение выражений (149.4) и (149.6) приводит к выводу, что падение напряжения 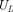 опережаетпофазеток /,
опережаетпофазеток /,

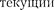 через катушку, на —, что и по- казано на векторной диаграмме (рис.
через катушку, на —, что и по- казано на векторной диаграмме (рис.
3.  Переменный ток, текущий через конденсатор емкостью С
Переменный ток, текущий через конденсатор емкостью С  0, 274
0, 274
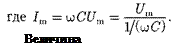
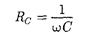
называется реактивным емкостным сопротивлением (или емкостным со- противлением). Для постоянного тока

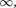
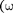 0)
0) 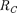 = т. е. постоянный ток че- рез конденсатор течь не может. Паде- ние напряжения на конденсаторе
= т. е. постоянный ток че- рез конденсатор течь не может. Паде- ние напряжения на конденсаторе
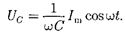 (149.8)
(149.8)
Сравнение выражений (149.7) и 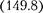 приводит к выводу, что падение напряжения
приводит к выводу, что падение напряжения 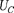 отстает по фазе от те-
отстает по фазе от те-
кущего через конденсатор тока 1 на —.
Это показано на векторной диаграмме (рис. 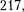 б).
б).
4.  Цепь переменного тока, содер- жащая последовательно включенные резистор, катушку индуктивности и конденсатор.На рис. 218, а представ- лен участок цепи, содержащий резистор сопротивлением R, катушку индуктив- ностью L конденсатор емкостью С, к концам которого приложено пере- менное напряжение (149.1). В цепи возникнет переменный ток, который вызовет на всех элементах цепи соот- ветствующиепадениянапряжения
Цепь переменного тока, содер- жащая последовательно включенные резистор, катушку индуктивности и конденсатор.На рис. 218, а представ- лен участок цепи, содержащий резистор сопротивлением R, катушку индуктив- ностью L конденсатор емкостью С, к концам которого приложено пере- менное напряжение (149.1). В цепи возникнет переменный ток, который вызовет на всех элементах цепи соот- ветствующиепадениянапряжения 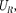
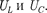
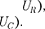
 На рис. 218,6 представлена вектор- ная диаграмма амплитуд падений на- пряжений на резисторе ( катушке (
На рис. 218,6 представлена вектор- ная диаграмма амплитуд падений на- пряжений на резисторе ( катушке ( 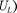 конденсаторе (
конденсаторе (
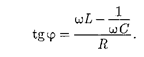
 Амплитуда
Амплитуда 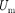 приложенного на- пряжения должна быть равна вектор- ной сумме амплитуд этих падений на- пряжений. Как видно из рис. 218, б, угол определяет разность фаз между напряжением и силой тока. Из рисун- ка следует, что [см. также формулу (147.16)]
приложенного на- пряжения должна быть равна вектор- ной сумме амплитуд этих падений на- пряжений. Как видно из рис. 218, б, угол определяет разность фаз между напряжением и силой тока. Из рисун- ка следует, что [см. также формулу (147.16)]
(149.9)
Из прямоугольного треугольника полу-
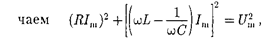
откуда амплитуда силы тока имеет зна- чение
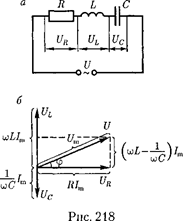
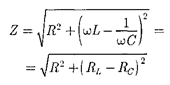
 где и
где и 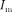 определяются соответственно формулами (149.9) и (149.10). Величина
определяются соответственно формулами (149.9) и (149.10). Величина
(149.12)
называется полным сопротивлением
цепи, а величина
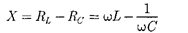
— реактивным сопротивлением.
Рассмотрим частный случай, когда в цепи отсутствует конденсатор. В дан- ном случае падения напряжений 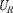 и
и 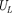 в сумме равны приложенному на- пряжению U. Векторная диаграмма для данного случая представлена на рис. 219, из которого следует, что
в сумме равны приложенному на- пряжению U. Векторная диаграмма для данного случая представлена на рис. 219, из которого следует, что
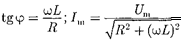
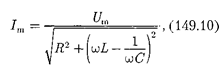 .(149.13)
.(149.13)
совпадающее с (147.15).
Следовательно, если напряжение в цепи изменяется по закону U =
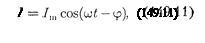 —
— 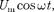 тов цепи течет ток
тов цепи течет ток
Рис.219
 275
275
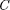 Выражения (149.9) и (149.10) совпа- дают с (149.13), если в них —— = 0, т.е.
Выражения (149.9) и (149.10) совпа- дают с (149.13), если в них —— = 0, т.е.
С= оо. Следовательно, отсутствие кон- денсатора в цепи означает, что С= оо, а не 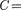 0. Данный вывод можно тракто- вать следующим образом: сближая об- кладки конденсатора до их полного со- прикосновения, получим цепь, в кото- рой конденсатор отсутствует [расстоя- ние между обкладками стремится к нулю, а емкость — к бесконечности; см. (94.3)].
0. Данный вывод можно тракто- вать следующим образом: сближая об- кладки конденсатора до их полного со- прикосновения, получим цепь, в кото- рой конденсатор отсутствует [расстоя- ние между обкладками стремится к нулю, а емкость — к бесконечности; см. (94.3)].
§ 150. Резонанс напряжений
Если вцепи переменного тока, со- держащей последовательно включен- ные конденсатор, катушку индуктивно- сти ирезистор (см. рис. 218),
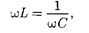 (150.1)
(150.1)
 то сдвиг фаз между током и напряже- нием (149.9) обращается в нуль
то сдвиг фаз между током и напряже- нием (149.9) обращается в нуль 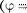 0), т.е. изменения тока и напряжения про- исходят синфазно. Условию (150.1) удовлетворяет частота
0), т.е. изменения тока и напряжения про- исходят синфазно. Условию (150.1) удовлетворяет частота
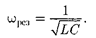 (150.2)
(150.2)
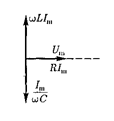
 В данном случае полное сопротивление цепи Z (149.12) становится минималь- ным, равным активному сопротивле- нию R цепи, и ток в цепи определяется этим сопротивлением, принимая мак- симальные (
В данном случае полное сопротивление цепи Z (149.12) становится минималь- ным, равным активному сопротивле- нию R цепи, и ток в цепи определяется этим сопротивлением, принимая мак- симальные (
