Механические и электромагнитные колебания

§ 140. Гармоническиеколебания и их характеристики

Колебаниями называются движе- ния или процессы, которые характери- зуются определенной повторяемостью во времени. Колебательные процессы широко распространены в природе и технике, например качание маятника часов, переменный электрический ток и т.д. При колебательном движении маятника изменяется координата его центра масс, в случае переменного тока колеблются напряжение и ток в цепи.

Физическая природа колебаний мо- жет быть разной, поэтому различают колебания механические, электромаг- нитные и др. Однако различные коле- бательные процессы описываются оди- наковыми характеристиками и одина- ковыми уравнениями. Отсюда следует целесообразность единого подхода к изучению колебаний различной физи- ческой природы. Например, единый под- ход к изучению механических и элект- ромагнитных колебаний применялся английским физиком Д.У.Рэлеем (1842-1919), А.Г.Столетовым, рус- ским инженером-экспериментатором П.Н.Лебедевым (1866-1912). Боль-

шой вклад в развитие теории колебаний внесли Л. И. Мандельштам (1879 — 1944) и его ученики.

Колебания называются свободны- ми (или собственными), если они со- вершаются за счет первоначально сооб- щенной энергии при последующем от- сутствии внешних воздействий на ко- лебательную систему (систему, совер- шающую колебания).

Простейшим типом колебаний яв- ляются гармонические колебания — колебания, при которых колеблющая- ся величина изменяется со временем по закону синуса (косинуса). Рассмотре- ние гармонических колебаний важно по двум причинам: 1) колебания, встреча- ющиеся в природе и технике, часто близки к гармоническим; 2) различные периодические процессы (процессы, повторяющиеся через равные проме- жутки времени) можно представить как наложение гармонических колебаний. Гармонические колебания величины s описываются уравнением типа

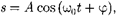(140.1)

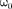где А — максимальное значение колеб- лющейся величины, называемое ампли- тудой колебания; — круговая (цик- лическая) частота.

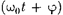Периодически изменяющийся аргу- мент косинуса называется фазой колебания. Она определяет сме- щение колеблющейся величины от по- ложения равновесия в данный момент времени t. Величина в уравнении гар- монических колебаний называется на- чальной фазой. Она определяет смеще- ние колеблющейся величины от поло- жения равновесия в начальный момент времени (t = 0).

Значение начальной фазы определя- ется выбором начала отсчета времени. Так как косинус изменяется в пределах от +1 до —1, то s может принимать зна- чения от +А до — А.

Определенные состояния системы, совершающей гармонические колеба- ния, повторяются через промежуток времени Т, называемый периодом ко- лебания, за который фаза колебания получает приращени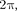е т. е.

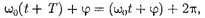
откуда

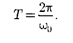(140.2)

Величина, обратная периоду колеба- ний,

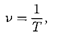(140.3)

т.е. число полных колебаний, совер- шаемых вединицу времени, называет- ся частотой колебаний. Сравнивая (140.2) и(140.3), получим

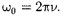Единица частоты — герц(Гц): 1 Гц —частота периодического процесса, при которой за 1с совершается один цикл процесса.

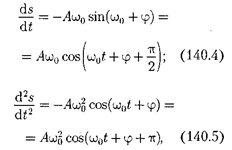Запишем первую и вторую произ- водные повремени от гармонически колеблющейся величины s:

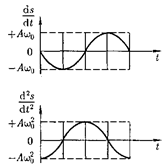Рис. 200

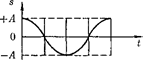
т.е. имеем гармонические колебания с той же циклической частотой. Амплиту- ды величин (140.4) и (140.5) соответ- ственно равны 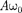и 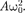Фаза величи-

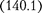
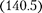
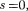ны (140.4) отличается от фазы величи- ны на 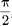, а фаза величины отличается от фазы величины (140.1) на тт. Следовательно, в моменты времени, когда 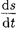приобретает наибольшие значения; когда s достигает максималь- ного отрицательного значения, то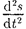

имеет наибольшее положительное зна-

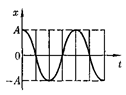
чение (рис. 200; начальная фаза = 0). Из выражения (140.5) следует диф- ференциальное уравнение гармони-

ческих колебаний

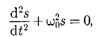(140.6)

Решением этого уравнения является выражение (140.1).

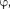
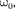
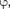
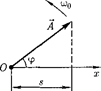
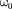Гармонические колебания изобра- жаются графически методом враща- ющегося вектора амплитуды, или методом векторных диаграмм. Для этого из произвольной точки О, выб- ранной на оси х, под углом равным начальной фазе колебания, откладыва- ется вектор 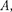модуль которого равен амплитуде А рассматриваемого колеба- ния (рис. 201). Если этот вектор приве- сти во вращение с угловой скоростью равной циклической частоте колеба- ний, то проекция конца вектора будет перемещаться по оси и принимать зна- чения от —А до А, а колеблющаяся ве- личина будет изменяться со временем по закону 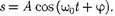Таким об- разом, гармоническое колебание мож- но представить проекцией на некото- рую произвольно выбранную ось векто- ра амплитуды 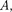отложенного из про- извольной точки оси под углом рав- ным начальной фазе, и вращающегося с угловой скоростью вокруг этой точки.

В физике часто применяется другой метод, который отличается от метода вращающегося вектора амплитуды лишь по форме. В этом методе колеблющую- ся величину представляют комплекс- ным числом. Согласно формуле Эйле- ра, для комплексных чисел

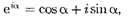(140.7)

где 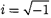—мнимая единица. Поэто- му уравнение гармонического колеба- ния (140.1) можно записать вкомплек- сной форме:

Рис.201

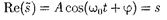представляет собой гармоническое ко- лебание. Обозначение Reвещественной части условимся опускать и (140.8) бу- дем записывать в виде

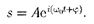
В теории колебаний принимается, что колеблющаяся величина s равна вещественнойчасти комплексного вы- ражения, стоящего в этом равенстве справа.

§ 141. Механические гармонические колебания

Пусть материальная точка соверша- ет прямолинейные гармонические ко- лебания вдоль оси координат х около положения равновесия, принятого за начало координат.

Тогда зависимость координаты х от времени t задается уравнением, анало- гичным уравнению (140.1), где s = х:

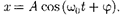(141.1)

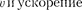
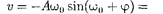Согласно выражениям (140.4) и (140.5), скорость о,колеб- лющейся точки соответственно равны

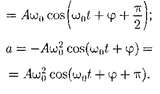
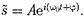(140.8)

Вещественная часть выражения (140.8)

(141.2)

Сила F= та, действующая на колеб- лющуюся материальную точку мас- т, с учетом (141.1) и 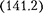равна

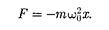
Следовательно, сила пропорцио- нальна смещению материальной точки из положения равновесия и направле- на в противоположную сторону (к по- ложению равновесия).

Кинетическая энергия материаль- ной точки, совершающей прямолиней- ные гармонические колебания, равна

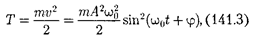
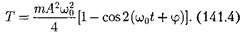
Потенциальная энергия матери- альной точки, совершающей гармони- ческие колебания под действием упру- гой силы F, равна

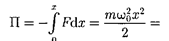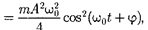(141.5)

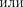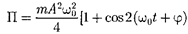(141.6)

Сложив (141.3) и (141.5), получим формулу для полной энергии:

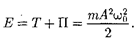(141.7)

Полная энергия остается постоян- ной, так как при гармонических коле- баниях справедлив закон сохранения механической энергии, поскольку упру- гая сила консервативна.

Рис. 202

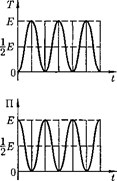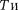
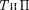Из формул (141.4) и (141.6) следу- ет, что П изменяются с частотой 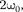т. е. с частотой, которая в два раза пре- вышает частоту гармонического коле- бания. 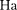рис. 202 представлены графи- ки зависимости х, от времени. Так

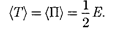
как (sin2 a) = (cos2 а) -, то из формул (141.3), (141.5) и (141.7) следует, что

§ 142. Гармонический осциллятор.Пружинный, физический и математический маятники

Гармоническим осциллятором на- зывается система, совершающая коле- бания, описываемые уравнением вида (140.6):

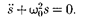(142.1)

Колебания гармонического осцил- лятора являются важным примером периодического движения и служат

точной или приближенной моделью вомногих задачах классической и кванто- вой физики. Примерами гармоническо- го осциллятора являются пружинный, физический и математический маятни- ки, колебательный контур (для токов и напряжений малых, что элемен- ты контура можно было бысчитать линейными; см. §146).

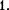Пружинныймаятник — это груз массой т, подвешенный наабсолютно упругой и совершающий гар- монические колебания под действием упругой силы F — 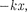где к — жест- кость пружины. Уравнение движения маятника вотсутствие сил трения

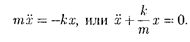
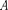Извыражений (142.1) и(140.1) сле- дует, что пружинный маятник соверша- ет гармонические колебания позакону х = 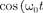+ 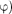с циклической час- тотой

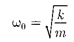(142.2)

и периодом

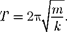(142.3)

Формула (142.3) справедлива для упругих колебаний в пределах, в кото- рых выполняется закон Гука [см. 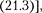т.е. когда масса пружины мала посрав- нению с массой тела.

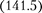Потенциальная энергия пружинно- го маятника, согласно и(142.2),

203

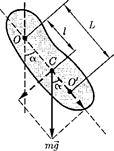дящей через точку О, не совпадающую с центром масс Стела (рис. 203).

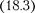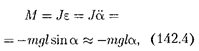
Если маятник отклонен из положе- ния равновесия на некоторый угол а, то в соответствии с уравнением динами- ки вращательного движения твердого тела в отсутствие сил трения вра- щающий момент М можно записать в ви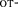де

где 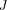—момент инерции маятника носительно оси, проходящей через точ- ку подвеса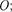 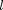— расстояние между ней и центром масс маятника.

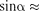Вращающий момент стремится вер- нуть маятник в положение равновесия ив этом отношении аналогичен упру- гой силе. Поэтому так же, как смеще- нию и упругой силе, моменту 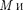уг- ловому смещению априписывают про- тивоположные знаки. При малых коле- баниях маятника (малых отклонениях маятника изположения равновесия) а.Тогда уравнение 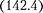мож-

но записать в виде

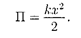
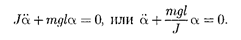
2. Физическиймаятник — это твер- дое тело, совершающее под действием силы тяжести колебания вокруг не- подвижной оси, прохо-

9 Курс физики

Принимая

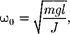(142.5)

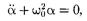получим уравнение Момент инерции математического маятника

идентичное с (142.1), решение которо- го [см. (140.1)] известно:

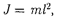
где / — длина маятника.

(142.8)

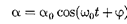I.(142.6)

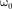Извыражения (142.6) следует, что при малых колебаниях физический ма- ятник совершает гармонические коле- бания с циклической частотой [см. (142.5)] и периодом

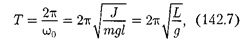J

где L = —- — приведенная длина фи-

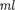
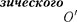маятника.

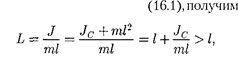Точка на продолжении прямой ОС, отстоящая от точки О подвеса ма- ятника нарасстоянии приведенной дли- ныL,называетсяцентромкачанийфи- зического маятника (см. рис. 203). При- меняя теорему Штейнера

т.е. 00' всегда больше ОС. Точка под- веса О маятника и центр качаний О' обладают свойством взаимозаменяе- мости: если точку подвеса перенести в центр качаний, то прежняя точка О под- веса станет новым центром качаний, и период колебаний физического маят- ника не изменится.

3. Математический маятник — это идеализированная система, состоя- щая из материальной точки массой т, подвешенной на нерастяжимой невесо- мой нити, и колеблющаяся под действи- ем силы тяжести.

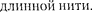Хорошим приближением математи- ческого маятника является небольшой тяжелый шарик, подвешенный на тон- кой

Так как математический маятник можно представить как частный случай физического маятника, предположив, что вся его масса сосредоточена в одной точке — центре масс, то, подставив вы- ражение (142.8) в формулу (142.7), по- лучим выражение для периода малых колебаний математического маятника

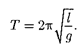(142.9)

Сравнивая формулы (142.7) и (142.9), видим, что если приведенная длина L физического маятника равна длине / математического маятника, то периоды колебаний этих маятников одинаковы. Следовательно, приведенная длина физического маятника — это длина такого математического маятника, пе- риод колебаний которого совпадает с периодом колебаний данного физичес- кого маятника.

§ 143. Свободные гармонические колебания в колебательном контуре

Среди различных физических явле- ний особое место занимают электро- магнитные колебания, при которых электрические величины (заряды, токи) периодически изменяются и которые сопровождаются взаимными превраще- ниями электрического и магнитного Для возбуждения и поддержа- ния электромагнитных колебаний ис- пользуется колебательный контур — цепь, состоящая из включенных после- довательно катушки индуктивностью L,

конденсатора емкостью С резистора сопротивлением R.

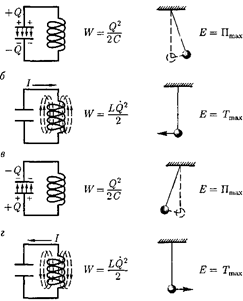
Рассмотрим последовательные ста- дии колебательного процесса в идеали- зированном контуре, сопротивление которого пренебрежимо мало (R 0). Для возбуждения в контуре колебаний конденсатор предварительно заряжают, сообщая его обкладкам заряды ± Q. Тог- да в начальный момент времени t = 0 (рис. 204, а) между обкладками конден- сатора возникнет электрическое поле,

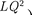энергия которого 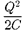[см. (95.4)]. Если замкнуть конденсатор на катушку ин- дуктивности, он начнет разряжаться, и в контуре потечет возрастающий со вре- менем ток /. В результате энергия элек- трического поля будет уменьшаться, а энергия магнитного поля катушки (она

равна ——) — возрастать.

Так как R 0, то, согласно закону сохранения энергии, полная энергия

204

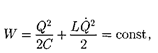так как она на нагревание не расходу- ется. Поэтому в момент t = Т ,когда

—

конденсатор полностью разрядится, энергия электрического поля обраща- ется в нуль, аэнергия магнитного поля (а следовательно, иток) достигает наи- большего значения (рис. 204, б). Сэто- го момента ток в контуре будет убывать, следовательно, начнет ослабевать маг- нитное поле катушки, и в ней будет ин- дуцироваться ток, который течет (со- гласно правилу Ленца) в том же направ- лении, что и ток разрядки конденсато- ра. Конденсатор начнет перезаряжать- ся, возникнет электрическое поле, стре- мящееся ослабить ток, который в кон- це концов обратится в нуль, азаряд на обкладках конденсатора достигнет мак- симума (рис. 204, в). Далее те же про- цессы начнут протекать в обратном на- правлении (рис. 204, система к мо- менту времени t — Гпридет в первона- чальное состояние (см. рис. 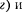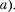204, Пос- ле этого начнется повторение рассмот- ренного цикла разрядки и зарядки кон- денсатора.

Если быпотерь энергии не было, то в контуре совершались быпериодичес- кие незатухающие колебания, т. е. пери- одически изменялись (колебались) бызаряд Q на обкладках конденсатора, напряжение U наконденсаторе и сила тока /, текущего через катушку индук- тивности. Следовательно, в контуре возникают электромагнитные колеба- ния, причем колебания сопровождают- ся превращениями 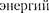электричес- кого и магнитного полей.

Электромагнитные колебания в ко- лебательном контуре можно сопоста- вить с механическим колебаниями ма- ятника (рис. 204), сопровождающими-

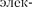
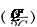ся взаимными превращениями потен- циальной и кинетической энергий ма- ятника. В данном случае энергия

трического поля конденсатора

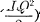аналогична потенциальной энергии ма- ятника, энергия магнитного поля ка-

тушки ( — энергии,

сила тока в контуре — скорости движе- ния маятника. Индуктивность L игра- ет роль массы т, а сопротивление кон- тура — роль силы трения, действующей на маятник.

Согласно закону Ома, для контура, содержащего катушку индуктивнос- тью L, конденсатор емкостью Си рези- стор сопротивлением R,

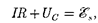
где IR — напряжение на резисторе;

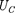= — — напряжение на конденсато-

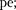
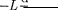
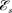— ЭДС самоиндукции,

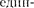возникающая в катушке при протека- нии в ней переменного тока —

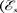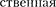ЭДС в контуре).

Следовательно,

ми. Тогда из (143.2) получим диффе- ренциальное уравнение свободных гар- монических колебаний заряда в контуре:

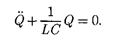
Из выражений (142.1) и (140.1) вы- текает, что заряд Q совершает гармони- ческие колебания по закону

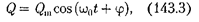
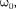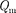где — амплитуда колебаний заряда конденсатора с циклической частотой называемой собственной часто-

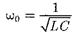той контура, т. е.

(143.4)

периодом

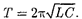(143.5)

Формула (143.5) впервые была по- лучена У.Томсоном и называется фор- мулой Томсона. Сила тока в колеба- тельном контуре [см. (140.4)]

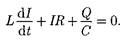(143.1)

Разделив (143.1) на L подставив

/ Q — Q, получим

dt

алыюе уравнение колебаний заряда Q

в контуре:

где амплитуда силы тока.

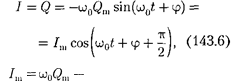Напряжение на конденсаторе

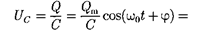
(143.7)

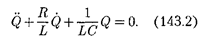где ния.

напряже-

В данном колебательном контуре внешние ЭДС отсутствуют, поэтому рассматриваемые колебания представ- ляют собой свободные колебания (см.

§ 140). Если сопротивление R — 0, то свободные электромагнитные колеба- ния в контуре являются гармонически-

Из выражений (143.3) и (143.6) вы-

текает, что колебания тока / опережа- ют по фазе колебания заряда Q на —,

т.е., когда ток достигает максимально- го значения, заряд (а также и напряже- ние [см. (143.7)] обращается в нуль, и наоборот.

§ 144. Сложение гармонических колебаний одного направления и одинаковой частоты. Биения

Колеблющееся тело может участво- вать в нескольких колебательных про- цессах, тогда необходимо найти резуль- тирующее колебание, иными словами, колебания необходимо сложить. Сло- жим гармонические колебания одного направления и одинаковой частоты:

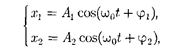воспользовавшись методом вращающе- гося вектора амплитуды (см. § 140). По- строим векторные диаграммы этих ко- лебаний (рис. 205). Так как векторы 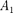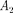вращаются с одинаковой угловой скоростью то разность фаз 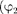— 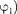между ними остается постоянной. Оче- видно, что уравнение результирующе-

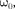го колебания будет

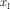х = 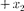= 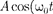+ 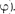(144.1)

В выражении (144.1) амплитуда А начальная фаза соответственно зада- ются соотношениями

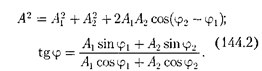
Таким образом, тело, участвуя в двух гармонических колебаниях одного на- правления и одинаковой частоты, совер- шает также гармоническое колебание в том же направлении и с той же часто- той, что и складываемые колебания. Амплитуда результирующего колеба- ния зависит от разности фаз 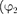— 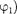складываемых колебаний.

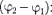Проанализируем выражение (144.2) в зависимости от разности фаз

Рис. 205

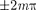1) - (т = 0, 1, 2, ...),

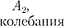тогда А = + т.е. амплитуда ре- зультирующего А равна сум- ме амплитуд складываемых колебаний;

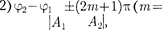= 0,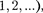

тогда А — — т.е. амплитуда ре- зультирующего колебания равна разно- сти амплитуд складываемых колебаний. Для практики особый интерес пред- ставляет случай, когда два складывае- мых гармонических колебания одина- кового направления мало отличаются по частоте. В результате сложения этих колебаний получаются колебания с пе- риодически изменяющейся амплиту- дой. Периодические изменения ампли- туды колебания, возникающие при сло- жении двух гармонических колебаний с близкими частотами, называются би-

Ениями.

Пусть амплитуды складываемых ко- лебаний равны А, а частоты равны и

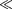
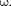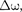+ причем 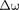Начало отсче- та выберем так, чтобы начальные фазы обоих колебаний были равны нулю:

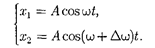Складывая эти выражения и учиты- вая, что 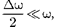найдем

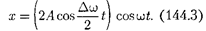
Результирующее колебание (144.3) можно рассматривать как гармониче-

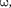ское с частотой амплитуда 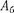кото- рого изменяется по следующему пери- одическому закону:

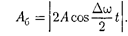(144.4)

Частота изменения 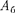в два раза больше частоты изменения косинуса (так как берется по модулю), т.е. час- тота биений равна разности частот складываемых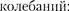

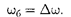
Период биений

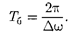Характер зависимости (144.3) пока- зан на рис. 206, где сплошные линии дают график результирующего колеба- ния (144.3), а огибающие их штрихо- вые — график медленно меняющейся по уравнению (144.4) амплитуды.

Определение частоты тона [звука оп- ределенной высоты (см. § 158)] биений между эталонным и измеряемым колеба- ниями— наиболееширокоприменяемый на практике метод сравнения измеряемой величины с эталонной. Метод биений используется для настройки музыкаль- ных инструментов, анализа слуха и т.д.

Любые сложные периодические ко- лебания s = f(t) можно представить в виде суперпозиции одновременно совер-

шающихся гармонических колебаний с различными амплитудами, различными начальными фазами, а также частотами, кратными циклической частоте

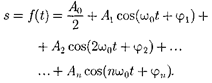
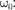(144.5)

Представление периодической фун- кции в виде (144.5) связывают с поня- тием гармонического анализа слож- ного периодического колебания, или разложения Фурье1. Слагаемые ряда Фурье, определяющие гармонические колебания с частотами на- зываются первой (или основной), вто- рой, третьей т. д. гармониками слож- ного периодического колебания.

§ 145. Сложение взаимно перпендикулярныхколебаний

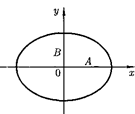
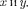Рассмотрим результат сложения двух гармонических колебаний одинаковой частоты происходящих во взаимно перпендикулярных направлениях вдоль осей Для простоты начало отсче- та выберем так, чтобы начальная фаза первого колебания была равна нулю, и запишем

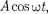х =

(145.1)

у =

где а — разность фаз обоих колебаний; А 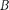— амплитуды складываемых ко- лебаний.

Уравнение траектории результиру- ющего колебания находится исключе- нием из выражений параметра t.

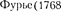
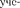Рис. 206

Ж. — 1830) — французский

Записывая складываемые колебания в виде

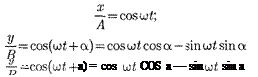В

заменяя во втором уравнении

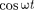X .

Рис. 208

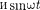на —на

А

получим пос-

(рис. 207, б). Результирующее колеба-

ле несложных преобразований уравне- ние эллипса, оси которого ориентирова- ны относительно координатных осей произвольно:

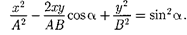(145.2)

Так как траектория результирующе- го колебания имеет форму эллипса, то такие колебания называются эллипти- ческиполяризованными.

Ориентация эллипса и размеры его осей зависят от амплитуд складывае- мых колебаний и разности фаз а. Рас- смотрим некоторые частные случаи, представляющие физический интерес: 1)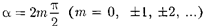

В данном случае эллипс вырождается в

отрезокпрямой

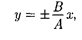(145.3)

где знак « + » соответствует нулю и четным значениям т (рис. 207, а), а знак « —» — нечетным значениям т

207

ние является гармоническим колебани-

ем с частотой и амплитудой 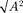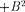, совершающимся вдоль прямой [см. (145.3)], составляющей с осью х угол

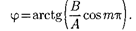Вданном случае

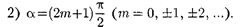
имеемделос поляризованны- миколебаниями;

В данном случае уравнение примет вид

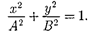(145.4)

Это уравнение эллипса, оси которого совпадают с осями координат, а его по- луоси равны соответствующим амп- литудам (рис. 208). Кроме того, если А = В, то эллипс [см. (145.4)] вырож- дается в окружность. Такие колебания называются поляризован- нымиколебаниями или колебаниями, поляризованными по кругу.

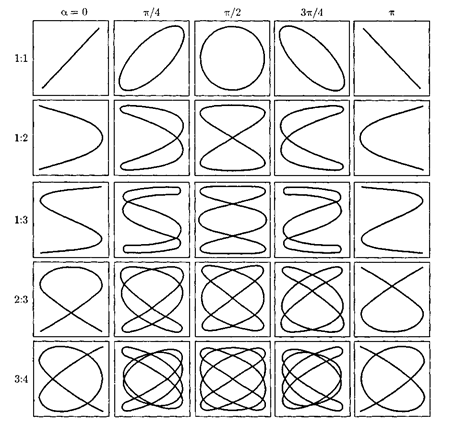
Если частоты складываемых взаим- но перпендикулярных колебаний раз- личны, то замкнутая траектория ре- зультирующего колебания довольно сложна. Замкнутые траектории, про- черчиваемые точкой, совершающей од- новременно два взаимно перпендику- лярных колебания, называются фигу- рами Вид этих кривых за- висит от соотношения амплитуд, частот и разности фаз складываемых колеба-

Ж. Лиссажу (1822-1880) - французский физик.

209

ний. На рис. 209 фигуры Лиссажу для различных

частот (указаны слева) и разностей фаз (указаны вверху; разность фаз прини- мается равной

Отношение частот складываемых колебаний равно отношению числа пе- ресечений фигур Лиссажу с прямыми, параллельными осям координат. По виду фигур можно определить неизве- стную частоту по известной или опре- делить отношение частот складывае- мых колебаний. Поэтому анализ фигур Лиссажу — широко используемый ме- тод исследования соотношений частот и разности фаз складываемых колеба- ний, а также формы колебаний.