Напряженность электростатического поля

Если в пространство, окружающее электрический заряд, внести другой за- ряд, то на него будет действовать куло- новская сила, следовательно в про- странстве, окружающем электрические

заряды, существует силовое поле. Со- гласно представлениям современной физики, поле реально существует и на- ряду с веществом является одной из форм существования материи, посред- ством которого осуществляются опре- деленные взаимодействия между мак- роскопическими телами или частица- ми, входящими в состав вещества. Вдан- ном случае говорят об электрическом поле —поле, посредством которого вза- имодействуют электрические заряды. Вданной главе будем рассматривать электрические поля, которые создают- ся неподвижными электрическими за- рядами и называются электростати- ческими.

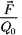Для обнаружения и опытного иссле- дования электростатического поля ис- пользуется пробный точечный поло- жительный заряд — такой заряд, ко- торый не искажает исследуемое поле (не вызывает перераспределения заря- дов, создающих поле). Если в поле, со- здаваемое зарядом Q, поместить проб- ный заряд Qo, то на него действует сила F, различная в разных точках ноля, ко- торая, согласно закону Кулона (78.2), пропорциональна пробному заряду Qo.

Поэтому отношение не зависит от

Qoи характеризует электростатическое поле в той точке, где пробный заряд находится. Эта величина называется напряженностью и является силовой характеристикой электростатическо - го поля.

Напряженность электростати- ческого поля в данной точке есть фи- зическая величина, определяемая си- лой, действующей на пробный единич- ный положительный заряд, помещен- ный в эту точку поля:

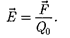(79.1)

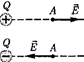Как следует из формул (79.1) и (78.1), напряженность поля точечного заряда в вакууме

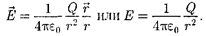(79.2)

Направление вектора Е совпадает с направлением силы, действующей на положительный заряд. Если поле созда- ется положительным зарядом, то век- тор Ё направлен вдоль радиуса-векто- ра от заряда во внешнее пространство (отталкивание пробного положитель- ного заряда); если иоле создается отри- цательным зарядом, то вектор Ё на- правлен к заряду (рис. 120).

Из формулы (79.1) следует, что еди- ница напряженности электростатиче- ского поля — ньютон на кулон(Н/Кл): 1 Н/Кл — напряженность такого поля, которое на точечный заряд 1 Кл дей- ствует с силой в 1 Н; 1 Н/Кл = 1 В/м, где В (вольт) — единица потенциала электростатического поля (см. § 84).

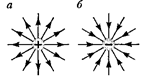
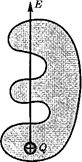
Графически электростатическое поле изображают с помощью линий на- пряженности — линии, касательные к которым в каждой точке совпадают с направлением вектора Ё (рис. 121). Им приписывается направление, совпадаю- щее с направлением вектора 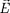в рас- сматриваемой точке линии. Так как в каждой данной точке пространства век- тор напряженности имеет лишь одно направление, то линии напряженности никогда не пересекаются.

Для однородного поля (когда век- тор напряженности в любой точке по- стоянен по модулю и направлению) ли- нии напряженности параллельны век- тору напряженности. Если поле созда- ется точечным зарядом, то линии на- пряженности — радиальные прямые, выходящие из заряда, если он положи- телен (рис. а), и входящие в него, если заряд отрицателен (рис. 121, б).

Рис. 120 Рис. 121

Вследствие большой наглядности гра- фический способ представления элек- тростатического поля широко применя- ется в электротехнике.

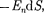Чтобы с помощью линий напряжен- ности можно было характеризовать не только направление, но и значение на- пряженности электростатического поля, условились проводить их с определен- ной густотой (рис. число линий напряженности, пронизывающих еди- ницу площади поверхности, перпенди- кулярную линиям напряженности, дол- жно быть равно модулю вектора Е. Тог- да число линий напряженности, прони- зывающих элементарную площадку dS, нормаль которой образует угол а с вектором Ё, равно 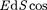a где 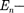проекция вектора Ё на нормаль п

площадке 123). Величина

называется потоком вектора напря- женности сквозь площадку dS. Здесь = dSn — вектор, модуль которого ра- вен dS, а направление совпадает с на- правлением нормали п площадке. Выбор направления вектора п (а следо- вательно, и dS) условен, так как его можно направить в любую сторону. Единицапотокавекторанапряженнос- тиэлектростатическогополя—вольт- метр(В•м).

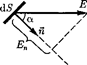Рис. 122 Рис. 123

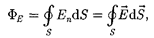Для произвольной замкнутой повер- хности S поток вектора Е сквозь эту поверхность

(79.3)

где интеграл берется по замкнутой по- верхности S. Поток вектора Е является алгебраической величиной: зависит не только от конфигурации поля Ё, но и от выбора направления Для замкну- тых поверхностей за положительное на- правление нормали принимается внеш- няя нормаль, т.е. нормаль, направлен- ная наружу области, охватываемой по- верхностью.

В истории развития физики имела место борьба двух теорий: дальнодей- ствия и близкодействия. В теории даль- нодействия принимается, что электри- ческие явления определяются мгновен- ным взаимодействием зарядов на лю- бых расстояниях. Согласно теории близкодействия, все электрические яв- ления определяются изменениями по- лей зарядов, причем эти изменения рас- пространяются в пространстве от точ- ки к точке с конечной скоростью.

Применительно к электростатичес- ким полям обе теории дают одинаковые результаты, хорошо согласующиеся с опытом. Переход же к явлениям, обус- ловленным движением электрических зарядов, приводит к несостоятельнос- ти теории дальнодействия, поэтому со- временной теорией взаимодействия за- ряженных частиц является теория близкодействия.

§ 80. Принцип суперпозиции электростатических полей.

Поле диполя

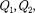Рассмотрим систему неподвижных точечных зарядов •••> 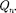Экспе-

риментально установлено, что сила вза- имодействия двух точечных зарядов не изменяется в присутствии других заря- дов. Тогда результирующая сила F, дей- ствующая со стороны поля на пробный заряд 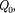равна векторной сумме сил 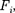приложенных к нему со стороны каж- дого из зарядов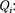

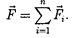(80.1)

Согласно (79.1), F = 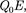где Е - напряженность результирующего поля, а 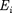—напряженность поля, создавае- мого зарядом 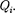Подставляя последние выражения в (80.1), получаем

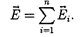(80.2)

Формула (80.2) выражает принцип суперпозиции (наложения) электро- статических полей, согласно которо- му напряженность Ё результирующего поля, создаваемого системой зарядов, равна геометрической сумме напряжен- ностей полей, создаваемых в данной точке каждым из зарядов в отдельности. Отметим, что принцип суперпози- ции является обобщением опытных данных и, возможно, нарушается на

малых расстояниях 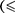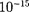м).

Принцип суперпозиции позволяет рассчитать электростатические поля любой системы неподвижных зарядов, поскольку если заряды не точечные, то их можно всегда мысленно разделить на малые части, считая каждую из них точечным зарядом.

Применим принцип суперпозиции для расчета электростатического поля электрического диполя. Электриче- ский диполь — система двух равных по модулю разноименных точечных заря- дов (+Q, — Q), расстояние 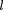между ко- торыми значительно меньше расстоя-

Рис. 124

ния до рассматриваемых точек поля. Вектор, направленный по оси диполя (прямой, проходящей через оба заряда) от отрицательного заряда к положи- тельному и равный расстоянию между ними, называется плечом диполя 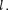Вектор

ля в точке А направлена по оси диполя и по модулю равна

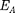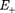= - Е_.

Обозначив расстояние от точки А до середины оси диполя через на осно- вании формулы (79.2) для случая ваку- ума можно записать

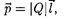(80.3)

совпадающий по направлению с плечом диполя и равный произведению заряда

\Q\ на плечо Г, называется электриче-

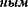ским моментом диполя или диполь- моментом(рис. 124).

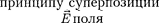Согласно

(80.2), напряженность диполя в произвольной точке

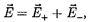
где 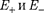— напряженности полей, со- здаваемых соответственно положитель- ным и отрицательным зарядами.

Воспользовавшись этой формулой, рассчитаем напряженность поля в про- извольной точке на продолжении оси диполя и на перпендикуляре к середи- не его оси.

1. Напряженность поля на продол- жении оси диполя в точке 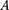(рис. 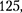а). Как видно из рисунка (рисунок не в масштабе), напряженность поля дипо-

Рис. 125

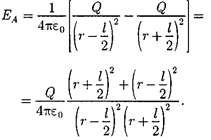Согласно определению диполя, поэтому

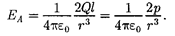
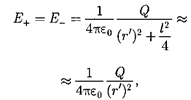
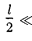
2. Напряженность поля на перпен- дикуляре, восставленном к оси из его середины, в точке В [рис. 125, б (рису- нок не в масштабе)]. Точка В равноуда- лена от зарядов, поэтому

(80.4)

где 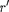— расстояние от точки В до сере- дины плеча диполя.

Из подобия равнобедренных треу- гольников, опирающихся на плечо ди- поля и вектор получим

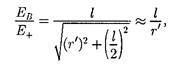
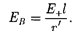
откуда

(80.5)

Подставив в выражение (80.5) зна- чение (80.4), получим

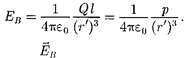
Вектор имеет направление, про- тивоположное вектору электрического момента диполя (вектор направлен от отрицательного заряда к положитель- ному).

§ 81. Теорема Гаусса дляэлектростатическогополя в вакууме

Вычисление напряженности поля системы электрических зарядов с помо- щью принципа суперпозиции электро- статических полей можно значительно упростить, используя выведенную не- мецким ученым К.Гауссом (1777 — 1855) теорему, определяющую поток вектора напряженности электрическо- го поля сквозь произвольную замкну- тую поверхность.

В соответствии с формулой (79.3) поток вектора напряженности сквозь сферическую поверхность радиуса охватывающую точечный заряд Q, на- ходящийся в ее центре (рис. 126), равен

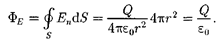
Этот результат справедлив для замк- нутой поверхности любой формы. Дей- ствительно, если окружить сферу (рис.

126) произвольной замкнутой поверх- ностью, то каждая линия напряженно- сти, пронизывающая сферу, пройдет и сквозь эту поверхность.

Рис. 126 Рис. 127

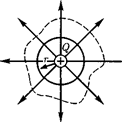
Если замкнутая поверхность произ- вольной формы охватывает заряд (рис. 127), то при пересечении любой выб- ранной линии напряженности с поверх- ностью она то входит в нее, то выходит из нее. Нечетное число пересечений при вычислении потока в конечном счете сводится к одному пересечению, так как поток считается положительным, если линии напряженности выходят из по- верхности, и отрицательным для ли- ний, входящих в поверхность. Если зам- кнутая поверхность не охватывает за- ряда, то поток сквозь нее равен нулю, так как число линий напряженности, входящих в поверхность, равно числу линий напряженности, выходящих из нее.

Таким образом, для поверхности любой формы, если она замкнута и зак- лючает в себя точечный заряд Q, поток

вектора Е будет равен —, т. е.

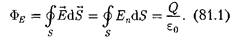Знак потока совпадает со знаком за- ряда Q.

Рассмотрим общий случай произ- вольной поверхности, окружающей п зарядов. В соответствии с принципом суперпозиции (80.2) напряженность Ё

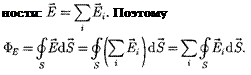поля, создаваемого всеми зарядами, равна сумме напряженностей 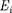полей, создаваемых каждым зарядом вотдель-

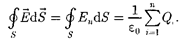Согласно (81.1), каждый из интегра- лов, стоящий под знаком суммы, равен 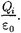Следовательно,

(81.2)

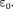Формула (81.2) выражает теоре- му Гаусса для электростатическо- го поля в вакууме: поток вектора на- пряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгеб- раической сумме заключенных внут- ри этой поверхности зарядов, делен- ной па Эта теорема выведена мате- матически для векторного поля лю- бой природы русским математиком 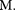В. Остроградским (1801-1862), а затем независимо от него примени- тельно к электростатическому полю — К. Гауссом.

В общем случае электрические заря-

ды могут быть «размазаны» с некото- рой объемной плотностью р =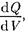

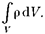различной в разных местах простран- ства. Тогда суммарный заряд, заклю- ченный внутри замкнутой поверхнос- ти S, охватывающей некоторый объем

V, равен Используя этот ре-

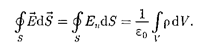зультат, теорему Гаусса (81.2) можно записать так:

§ 82. Применение теоремы Гаусса к расчету некоторых электростатических полей в вакууме

1. 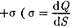Поле равномерно заряженной беско- нечной плоскости.Бесконечная плоскость (рис. 128) заряжена с постоянной поверх- ностной плотностью — за- ряд, приходящийся на единицу поверхнос- ти). Линии напряженности перпендикуляр- ны рассматриваемой плоскости и направле- ны от нее в обе стороны.

В качестве замкнутой поверхности мыс- ленно построим цилиндр, основания кото- рого параллельны заряженной плоскости, а ось перпендикулярна ей. Так как образую-

щие цилиндра параллельны линиям напря- женности (cos = 0), то поток вектора на- пряженности сквозь боковую поверхность цилиндра равен нулю, а полный поток сквозь цилиндр равен сумме потоков сквозь его основания (площади оснований равны и для основания 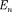совпадает с Е), т.е. ра- вен 2ES. Заряд, заключенный внутри пост- роенной цилиндрической поверхности, ра- вен 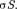Согласно теореме Гаусса (81.2),

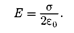
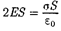,откуда

(82.1)

Следует отметить, что это формула спра- ведлива только для малых (по сравнению с размерами плоскости) расстояний от плос- кости, так как только тогда плоскость мож- но считать бесконечной. Из формулы (82.1) следует, что поле равномерно заряженной плоскостиоднородно.

2. Поледвух бесконечных параллель- ных разноименно заряженных плоскостей(рис. 129). Пусть плоскости заряжены рав-

Рис. 128

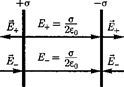Рис. 129

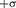
разноименными зарядами с повер- хностными плотностями и Поле та- ких плоскостей найдем как суперпозицию полей, создаваемых каждой из плоскостей в отдельности. На рисунке верхние стрелки соответствуют полю от положительно заря- женной плоскости, нижние — от отрица- тельно заряженной. Слева и справа от плос- костей поля вычитаются (линии напряжен- ности направлены навстречу друг другу), поэтому здесь напряженность поля Е = 0. 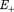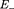Вобласти между плоскостями Е — + 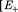и Е_ определяются по формуле (82.1)].

Поэтому результирующая напряженность

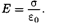(82.2)

Таким образом, результирующая напря- женность поля в области между плоскостя- ми описывается формулой (82.2), а вне объема, ограниченного плоскостями, равна нулю.

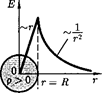
3. 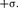Поле равномерно заряженной сфе- рической поверхности.Сферическая по- верхность радиусом R с общим зарядом Q заряжена равномерно с поверхностной плотностью Благодаря равномерному распределению заряда по поверхности поле, создаваемое им, обладает сферической сим- метрией. Поэтому линии напряженности направлены радиалыю (рис. 130). Построим мысленно сферу радиусом г, имеющую об-

щий центр с заряженной сферой. Если > R, то внутрь поверхности попадает весь заряд Q, создающий рассматриваемое поле, и, по те- ореме Гаусса (81.2), 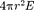= —, откуда

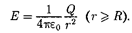(82.3)

При r> R поле убывает с расстоянием по такому же закону, как у точечного заря- да. График зависимости 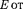приведен на рис. 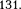Если 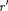< R, то замкнутая поверх- ность не содержит внутри зарядов, поэтому внутри равномерно заряженной сферичес- кой поверхности электростатическое поле отсутствует (Е— 0).

4.Полеобъемнозаряженногошара.Шар радиусом R с общим зарядом Q заряжен рав-

—

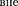заряд, приходящийся на единицу объема). Учитывая соображения симметрии (см. п. 3), можно показать, что для напряженно- сти поля шара получится тот же резуль- тат, что и в предыдущем случае [см. (82.3)]. Внутри шара напряженность поля будет другая. Сфера радиусом 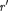< R. охватывает за-

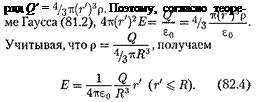
Таким образом, напряженность поля вне равномерно заряженного шара описывает- ся формулой (82.3), а внутри него изменяет- ся линейно с расстоянием 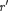согласно выра- жению (82.4). График зависимости 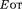для рассмотренного случая приведен на рис.

5. Поле равномерно заряженного беско- нечного цилиндра (нити).Бесконечный ци- линдр радиусом R (рис. заряжен равно-

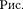132

Рис.130 Рис. 131

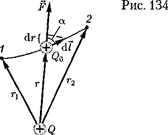
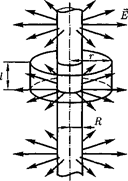Рис. 133

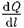мерно с линейной плотностью т (т = —

заряд, приходящийся на единицу длины). Из соображений симметрии следует, что ли- нии напряженности будут направлены по радиусам круговых сечений цилиндра с оди- наковой густотой во все стороны относи- тельно оси цилиндра.

В качестве замкнутой поверхности мыс- ленно построим коаксиальный цилиндр ра- диусом и высотой (см. рис. 133). Поток вектора Е сквозь торцы коаксиального ци- линдра равен нулю (торцы параллельны ли- ниям напряженности), а сквозь боковую по- верхность равен 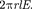По теореме Гаусса

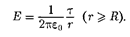(81.2), при 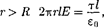откуда

(82.5)

Если < 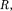то замкнутая поверхность за- рядов внутри не содержит, поэтому в этой области Е = 0. Таким образом, напряжен- ность поля вне равномерно заряженного бесконечного цилиндра определяется выра- жением (82.5), внутри же его поле отсут- ствует.

§ 83. Циркуляция вектора напряженности электростатического поля

Если в электростатическом поле то- чечного заряда Q из точки 1 в точку 2

вдоль произвольной траектории (рис.

134) перемещается другой точечный за- ряд 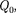то сила, приложенная к заряду, совершает работу. Работа силы F на элементарном перемещении 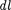равна

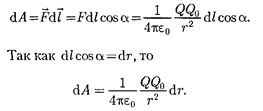
Работа при перемещении заряда 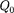из точки 1 вточку 2

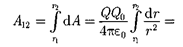
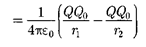(83.1)

не зависит от траектории перемещения, а определяется только положениями начальной 1 и конечной 2 точек. Сле- довательно, электростатическое поле точечного заряда является потенци- альным, а электростатические силы — консервативными (см. § 12).

Из формулы (83.1) следует, что ра- бота, совершаемая при перемещении электрического заряда во внешнем электростатическом поле по любому замкнутому пути L, равна нулю, т. е.

(83.2)

Если в качестве заряда, переносимо- го в электростатическом поле, взять единичный точечный положительный заряд, то элементарная работа сил поля на пути 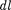равна 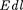— 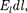где =

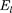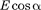= — проекция вектора Ё на на- правление элементарного перемеще- ния. Тогда формулу (83.2) можно запи- сать в виде

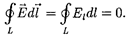(83.3)

Интеграл 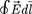= 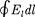называет-

L L

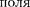ся циркуляцией вектора напряжен- ности. Таким образом, циркуляция вектора напряженности электростати- ческого вдоль любого замкнутого контура равна нулю. Силовое поле, об- ладающее свойством (83.3), называет- ся потенциальным. Из обращения в нуль циркуляции вектора Е следует, что линии напряженности электроста- тического поля не могут быть замкну- тыми, они начинаются и кончаются на зарядах (соответственно на положи- тельных или отрицательных) или же уходят в бесконечность.

Формула (83.3) справедлива только для электростатического поля. В даль- нейшем будет показано, что для поля движущихся зарядов (поля, изменяю- щегося со временем) условие (83.3) не выполняется (для него циркуляция вектора напряженности отлична от нуля).

§84. Потенциал электростатического поля

Тело, находящееся в потенциальном поле сил (а электростатическое поле является потенциальным), обладает потенциальной энергией, за счет кото- рой силами поля совершается работа

(см. § 12). Работа консервативных сил совершается за счет убыли потенциаль- ной энергии [см. (12.2)]. Тогда работу (83.1) сил электростатического поля можно представить как разность потен- циальных энергий, которыми обладает точечный заряд 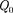в начальной и конеч- ной точках поля заряда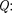

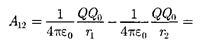
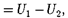(84.1)

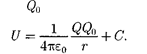откуда следует, что потенциальная энер- гия заряда в поле заряда Q равна

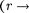
Потенциальная энергия 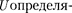ется с точностью до постоянной С. Зна- чение постоянной обычно выбирается так, чтобы при удалении заряда на бес- конечность оо) потенциальная энергия обращается в нуль ( U= 0), тог- да С = 0 и потенциальная энергия за- ряда 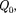находящегося в поле заряда Q на расстоянии от него, равна

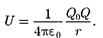(84.2)

Для одноименных зарядов 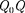> 0 и потенциальная энергия их взаимодей- ствия (отталкивания) положительна, для разноименных зарядов 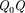< 0 и потенциальная энергия их взаимодей- ствия (притяжения) отрицательна.

Если поле создается системой п то- чечных зарядов 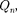то работа электростатических сил, совершаемая над зарядом 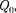равна алгебраической сумме работ сил, обусловленных каж- дым из зарядов в отдельности. Поэто- му потенциальная энергия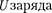 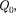находящегося в этом поле, равна сум- ме потенциальных энергий 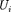каждого из зарядов:

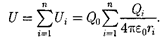(84.3)

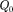Из формул (84.2) и (84.3) вытекает, что отношение — не зависит от 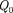и

является энергетической характерис- тикойэлектростатическогополя,назы- ваемой потенциалом:

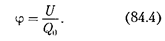
Потенциал в какой-либо точке электростатического поля есть физиче- ская величина, определяемая потенци- альной энергией единичного положи- тельного заряда, помещенного в эту точку. Из формул (84.4) и (84.2) следует, что потенциал поля, создаваемого то-

чечным зарядом Q, равен

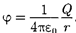(84.5)

Работа, совершаемая силами элект- ростатического поля при перемещении заряда 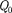ИЗ ТОЧКИ 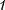в точку 2 [см. (84.1), (84.4), (84.5)], может быть представле- на как

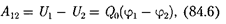
т. е. равна произведению перемещаемо- го заряда на разность потенциалов в начальной и конечной точках.

Разность потенциалов двух точек 1 в 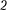в электростатическом поле определя- ется работой, совершаемой силами поля, при перемещении единичного положи- тельного заряда из точки 1 в точку 2.

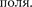При решении конкретных задач фи- зический смысл имеет разность потенци- алов между двумя точками электроста- тического

Работа сил поля при перемещении заряда 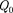ИЗ ТОЧКИ 1 в точку 2 может быть записана также в виде

(84.7)

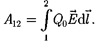Приравняв (84.6) и(84.7), придем к

выражению для разности потенциалов:

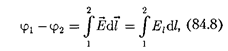где интегрирование можно произво- дить вдоль любой линии, соединяющей начальную и конечную точки, так как работа сил электростатического поля не зависит от траектории перемещения.

Если перемещать заряд 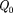из произ- вольной точки запределы поля, т. е. на бесконечность, где, поусловию, потен- циал равен нулю, то работа сил элект- ростатического поля, согласно (84.6), 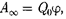откуда

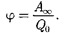(84.9)

Таким образом, потенциал — физи- ческая величина, определяемая рабо- той по перемещению единичного поло- жительного заряда при удалении его из данной точки поля на бесконечность. Эта работа численно равна работе, со- вершаемой внешними силами (против сил электростатического поля) по пе- ремещению единичного положитель- ного заряда из бесконечности в данную точку поля.

Из выражения (84.4) и (84.6) следу- ет, что единица потенциала иразности потенциалов — вольт (В): 1 В — потен- циал такой точки поля, в которой заряд в 1 Кл обладает потенциальной энер- гией 1 Дж (1 В = 1 Дж/Кл). Учитывая размерность вольта, можно показать, что введенная в § 79 единица напряжен- ности электростатического поля дей- ствительно равна 1 В/м: 1 Н/Кл —

= •м/(Кл • м)= •м) 1 В/м.

Из формул (84.3) и (84.4) вытекает, что если поле создается несколькими зарядами, то потенциал поля системы зарядов равен алгебраической сумме потенциалов полей всех этих зарядов:

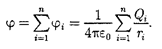§85.Напряженность как градиент потенциала.