Магнитный поверхностный эффект в плоском листе

Переменное электромагнитное поле быстро за­тухает по мере проникновения в толщу проводящей среды. Это приводит к не­равномерному распреде­лению поля по сечению магнитопровода, и следова­тельно, к неравномерному распределе­нию магнитного потока по сечению: на оси магнитопровода плотность магнитного потока наименьшая, а у поверхно­сти — наибольшая.

Для более равномерного распределения магнитного потока по сечению магнитопро­вода и для уменьшения потерь на вихревые токи, магнитопроводы трансформаторов соби­раются из отдельных тонких листов электротехнической стали, изолированных друг от друга. Исследуем распространение переменного поля в таком листе.

Рассмотрим поле в стальном листе при прохождении вдоль листа переменного магнитного потока .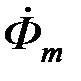

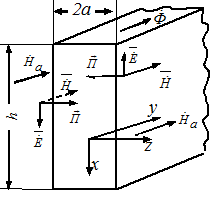
Рис.5.1

Лист (рис.5.1) имеет толщину 2а, высоту h (h >> 2а) и весьма большую протяженность в направлении, перпендикулярном рисунку. Средняя плотность магнитного потока по сечению листа

.

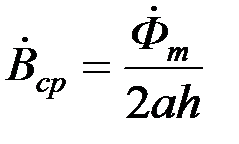Задача состоит в определении законов изменения 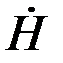и Ė по сечению листа. В силу симметрии Напряжённость магнитного поля на поверхности листа на левой и на правой поверхностях листа одинаковы. Обозначим ее через 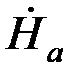и будем полагать известной (в дальнейшем выразим ее через ).

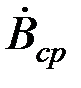Так как толщина листа 2а много меньше высоты листа h, то искажающим влиянием краев листа можно в первом приближении пренебречь и считать, что в лист с двух сторон проникает плоская электромагнитная волна.

Расположим оси координат декартовой системы в соответствии с рис. 5.1. Примем, как и прежде, 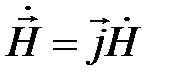. Общее решение для 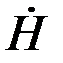таково

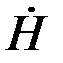=Ċ₁e^pz+Ċ₂e^-pz.

Из граничных условий найдем постоянные интегрирования. Для точек, находящихся на левой стороне листа, т.е.:

при z = –а 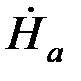= Ċ₁e^-pа+ Ċ₂e^pа; (5.1)

при z = + а 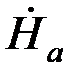= Ċ₁e^pа+ Ċ₂e^-ра. (5.2)

Совместное решение уравнений (5.1) и (5.2) относительно Ċ₁ и Ċ₂дает Ċ₁= Ċ₂= 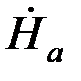/( e^pа+ e^-pа)= 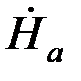/2ch pa.

Следовательно, в произвольной точке

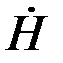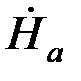= /2ch pa·( e^pz+ e^-pz)= 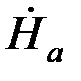ch pz/ ch pa. (5.3)

Напряжённость электрического поля

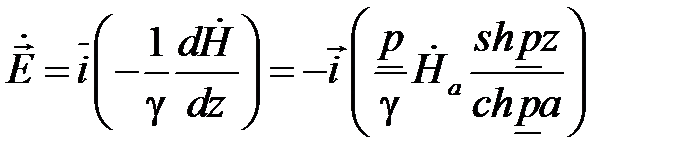(5.4)

Вектор Пойнтинга направлен к средней плоскости листа (внутрь листа), т.е. поток энергии электромагнитного поля поступает из диэлектрика внутрь листа.

Ток, возникающий при прохождении по листу переменного магнитного потока называют вихревым током. Вектор плотности этого тока 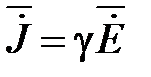в любой точке листа коллинеарен с вектором 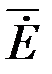в этой же точке и изменяется по тому же закону (5.4).

Магнитная индукция 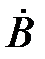в произвольной точке

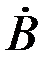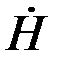=μ = μ 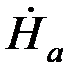сh pz/ch pa.

Среднее значение магнитной индукции в листе

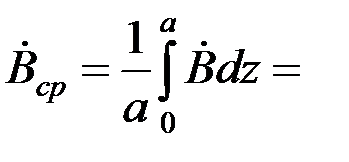(μ 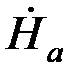sh pа) /(apch pa) = (μ 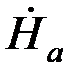th pa) /ap. (5.5)

Если считать 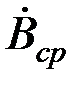известной и равной 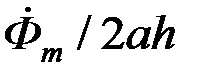, то из выражения (5.5) может быть найдена Напряжённость поля 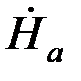на поверхности листа

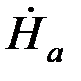=ap 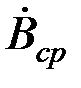/(μ th pa).

Отношение среднего значения магнитной индукции по сечению листа 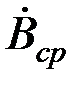к напряженности поля на поверхности листа 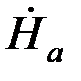называют комплексной магнитной проницаемостью и обозначают .

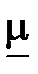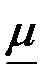=(μ th pa)/ар ( = ).

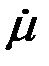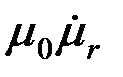При больших значениях pа имеем th pa »1 и комплексная магнитная проницаемость 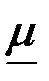оказывается равной 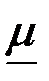= 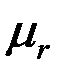/ ра.

Явление неравномерного распределения поля по сечению проводящего тела, вызванное затуханием электромагнитной волны, называют поверхностным эффектом. Если вдоль листа направлен магнитный поток, то поверхностный эффект часто называют магнитным, если вдоль плоской шины направлен переменный ток, то наблюдающийся при этом поверхностный эффект часто называют электрическим поверхностным эффектом.

Природа их одна и та же.

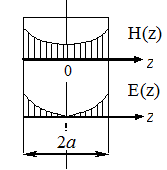
Рис.5.2

На рис.5.2 построены две кривые. Первая из них дает характер изменения модуля напряженности магнитного поля в функции от z. В средней плоскости листа Н до нуля не снижается, так как ch 0≠0. Кривая H (z) строится по уравнению (6.14). Вторая кривая на рис.5.2 дает характер изменения модуля напряженности электрического поля в функции от z. Кривая плотности вихревых токов 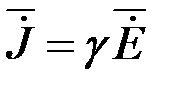качественно повторяет кривую Ė от z (разница только в масштабе).