Соответствия электростатического (электрического) поля и магнитного поля постоянного тока
Проведем уравнения и граничные условия для электростатического поля, электрического поля в проводящей среде, а также магнитного поля постоянного тока в области, где нет токов ( 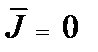 ), в однородной изотропной среде. Результаты сравнения представлены в табл.4.1.
), в однородной изотропной среде. Результаты сравнения представлены в табл.4.1.
Т а б л и ц а 4.1
| № п/п | Электростатическое поле | Электрическое поле в проводящей среде | Магнитное поле постоянного тока |
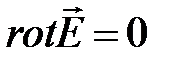 | 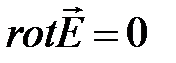 | 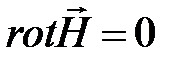 , , | |
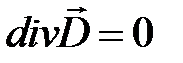 | 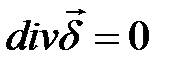 | 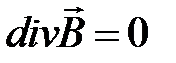 | |
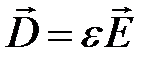 | 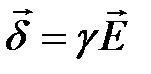 | 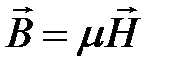 | |
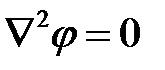 | 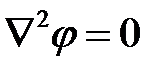 | 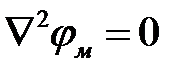 | |
1) 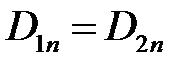 2) 2) 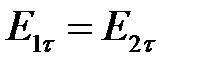 . . | 1) 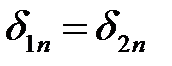 2) 2) 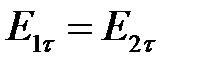 | 1) 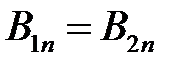 , 2) , 2) 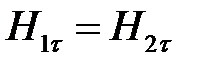 . . |
Здесь необходимо также упомянуть о двух типах взаимного соответствия электростатического (электрического) поля и магнитного поля постоянного тока в областях, не занятых током.
Первый тип соответствия возникает, когда распределения линейных зарядов в электростатическом поле и линейных токов в магнитном поле одинаковы.
Т а б л и ц а 4.1
| № п/п | Электростатическое поле | Электрическое поле в проводящей среде | Магнитное поле постоянного тока |
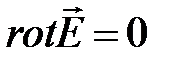 | 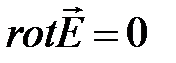 | 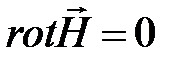 , , | |
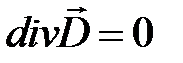 | 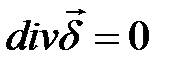 | 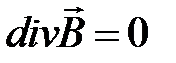 | |
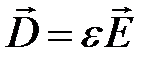 | 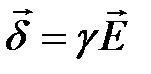 | 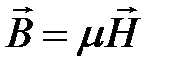 | |
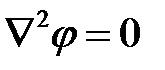 | 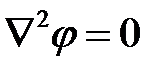 | 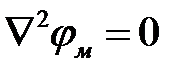 | |
1) 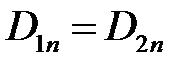 2) 2) 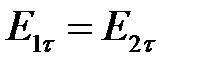 . . | 1) 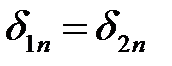 2) 2) 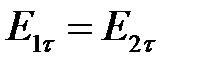 | 1) 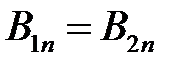 , 2) , 2) 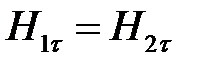 . . |
В табл.4.2 приведены решения для электростатического поля линейного заряда и магнитного поля линейного тока.
Таблица.4.2
| Электростатическое поле | Магнитное поле |
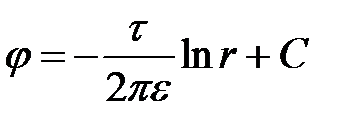 | 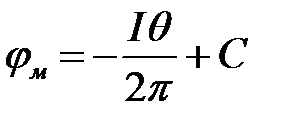 |
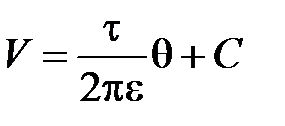 | 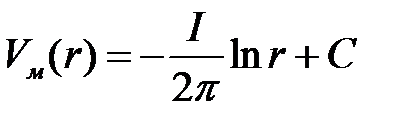 |
В этом случае соответствуют картины электростатического и магнитного полей (рис. 4.7).
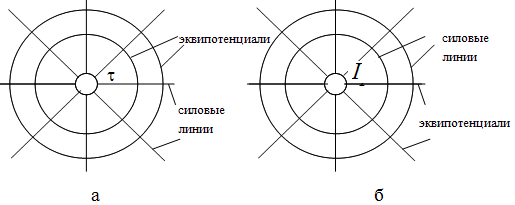
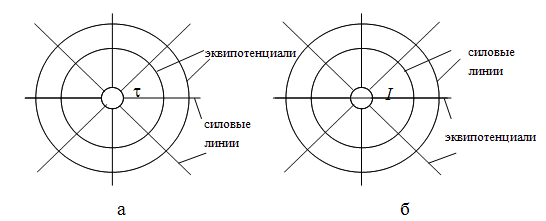
Рис. 4.7. К соответствию электростатического и магнитногополя
Различие между ними заключается лишь в том, что на месте линий напряженности электрического поля располагаются линии равного магнитного потенциала и на месте линий равного электрического потенциала располагаются линии напряженности магнитного поля.
Второй тип соответствия возникает, когда одинакова форма граничных эквипотенциальных поверхностей в электростатическом поле и в магнитном поле постоянного тока. В этом случае картины поля оказываются совершенно одинаковыми.
Рассмотренные свойства магнитного поля постоянного тока расширяют область применения метода электростатической аналогии: при расчёте магнитного поля в области вне проводников с постоянными токами можно воспользоваться готовыми аналитическими решениями соответствующих задач электростатики и электрического поля в проводящей среде.
Поток вектора Пойтинга в коаксиальном кабеле
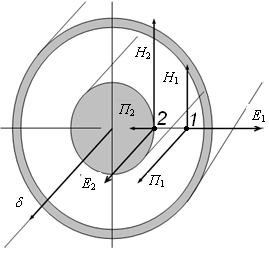
К кабелю (рис.4.8) приложено постоянное напряжение U и протекает ток I.
Особенностью режима работы коаксиального кабеля является то, что его электрическое и магнитное поле не выходит за пределы наружной оболочки.
Рассмотрим режим точки 1, расположенной в диэлектрике на расстоянии r от оси кабеля. Линейная плотность заряда: 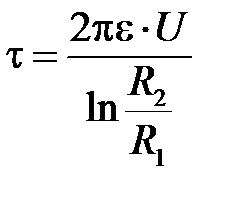 .Радиальная составляющая напряженности электрического поля:
.Радиальная составляющая напряженности электрического поля:
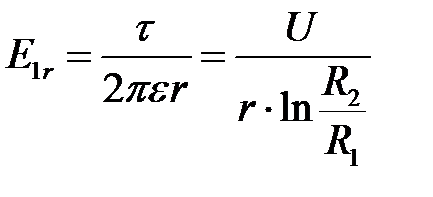
 .
.
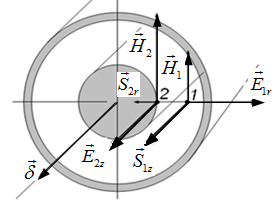
Рис.4.8. Коаксиальный кабель
Вектор напряженности магнитного поля имеет только угловую составляющую : 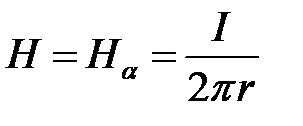 .
.
Векторы поля 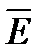 и
и 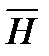 направлены под углом в 90о друг к другу.
направлены под углом в 90о друг к другу.
Вектор Пойтинга: 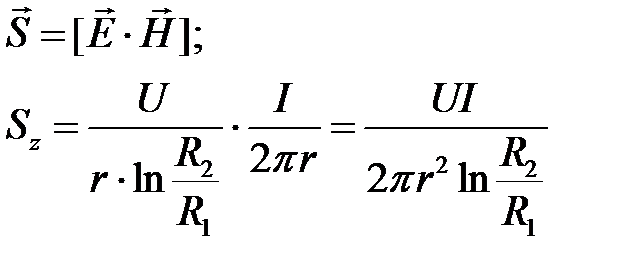 .
.
Поток вектора Пойтинга через поперечное сечение диэлектрика:
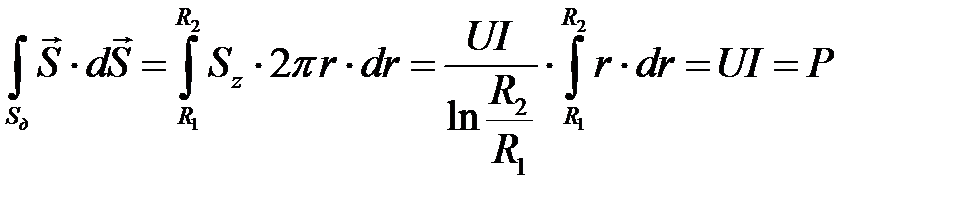 .
.
Поток вектора Пойтинга через поперечное сечение диэлектрика равен передаваемой мощности Р, т. е. энергия от источника к приемнику передается электромагнитным полем, сосредоточенным в диэлектрике между жилой и оболочкой.
Рассмотрим режим точки 2, расположенной на наружной поверхности жилы.
Плотность тока в жиле кабеля: 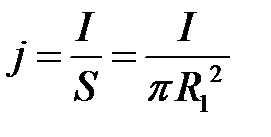 .
.
Составляющая напряженности электрического поля по оси z: 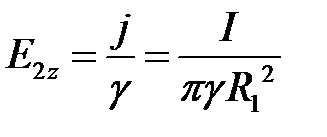 .
.
Напряжённость магнитного поля: 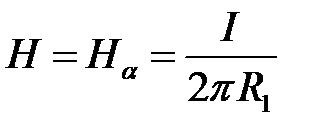 .
.
Векторы поля 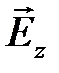 и
и 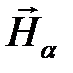 направлены под углом в 90о друг к другу.
направлены под углом в 90о друг к другу.
Радиальная составляющая вектора Пойтинга: 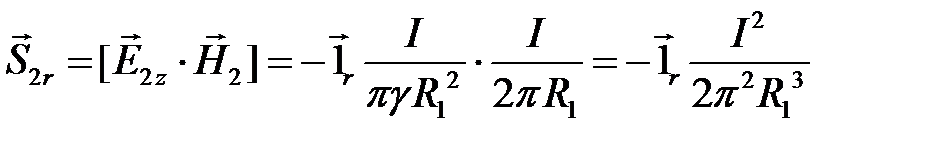 .
.
Поток вектора Пойтинга через боковую поверхность внутренней жилы:
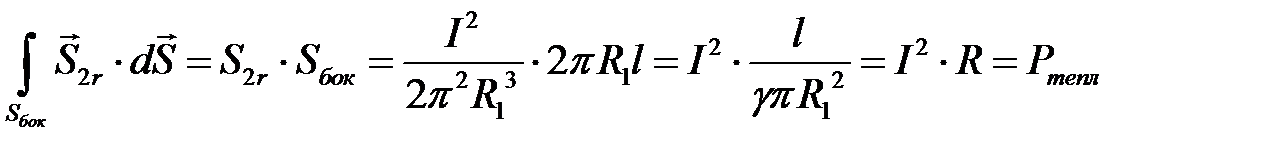 .
.
Поток вектора Пойтинга через наружную поверхность жилы направлен внутрь провода и равен мощности тепловых потерь в жиле.
