Метод средних потенциалов для расчёта потенциальных коэффициентов и емкостей ёмкостей в системе проводов

В электростатическом поле потенциал проводника одинаков во всех его точках, заряд же распределяется по поверхности проводника неравномерно.

В методе методом средних потенциалов полагается, что заряд распределяется равномерно по поверхности проводников и для линейных проводников — равномерно по их длине. Вычисляется распределение потенциала по поверхности или по длине проводников, и в формулу для емкости вводится среднее значение вычисленных таким образом потенциалов проводников. Этот метод в ряде случаев, например при вычислении емкости системы, образованной параллельными проводами, дает достаточно точные результаты. Объясняется это тем, что неравномерность распределения заряда заметно сказывается лишь на концах таких проводов.

Предположим, что имеются два отрезка проводов, длины которых l₁ и l₂ (рис.2.18). Требуется вычислить потенциальный коэффициент α₁₂. Предположим, что q₁ = 0 и q₂ = 0. При этом имеем 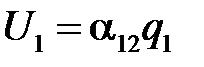. Полагаем, что заряд q₂ распределен равномерно вдоль второго провода с линейной плотностью τ₂ = q₂/l₂.

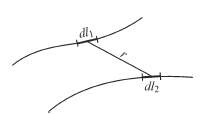
Рис.2.18

Потенциал в некоторой точке первого провода, определяемый зарядом q₂, будет равен

.

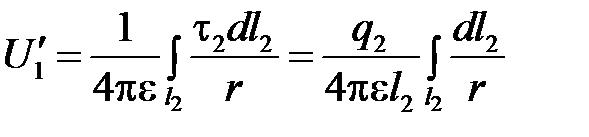причем интегрирование производится вдоль всего второго провода. Среднее значение потенциала первого провода получается в результате интегрирования вдоль первого провода:

.

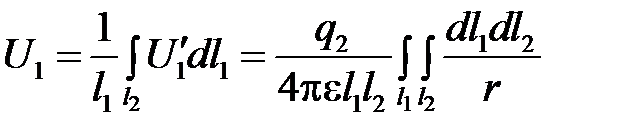Таким образом, искомый потенциальный коэффициент определяется формулой

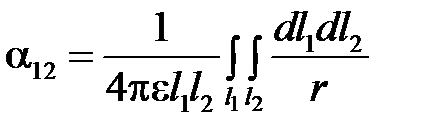
Выражение для потенциального коэффициента с одинаковыми индексами, например α₁₁ для прямолинейного отрезка провода круглого сечения, может быть найдено путем следующих рассуждений. Предполагаем соответственно принятому допущению, что заряд, находящийся на поверхности провода, равномерно распределен по длине провода. Находим потенциал 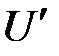, создаваемый этим зарядом в разных точках оси провода, и вычисляем среднее значение U потенциала вдоль оси. Пусть r — расстояние от кольцевого элемента поверхности проводника, имеющего длину 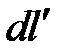в направлении оси проводника (рис.2.19), до элемента dl оси проводника, l — длина проводника и r₀ — радиус его сечения. Потенциал 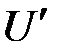в некоторой точке оси, определяемый всем зарядом q проводника, равен

.

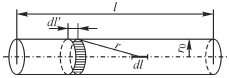
Рис.2.19

Среднее значение потенциала вдоль всей оси будет

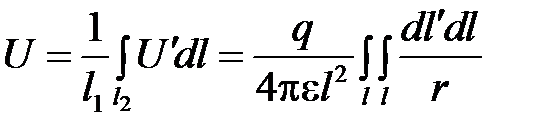
Следовательно,

.

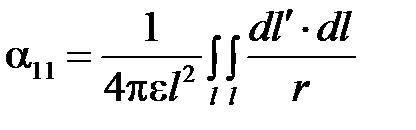причем наименьшее значение r есть r₀.

В качестве примера определим, пользуясь методом средних потенциалов, потенциальный коэффициент α₁₂ для параллельных отрезков проводов, расположенных на расстоянии D друг от друга и имеющих одинаковые длины l₁ = l₂ = l, причем начала отрезков лежат на одном перпендикуляре к ним. Оси координат расположим так, как показано на рис.2.20.

Имеем

.

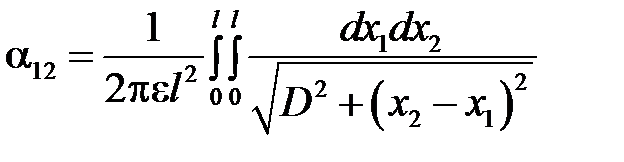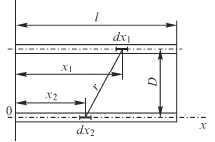
Рис.2.20

После вычислений, получим

.

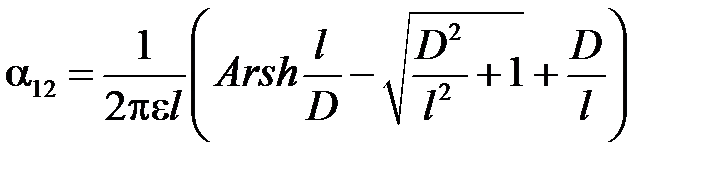При вычислении коэффициентов α₁₁ и α₂₂ с одинаковыми индексами для прямолинейного проводника, имеющего круглое сечение радиуса r₀, результат интегрирования приведет к формуле, которая получается из только что полученной формулы путем замены D на r₀. Следовательно,

.

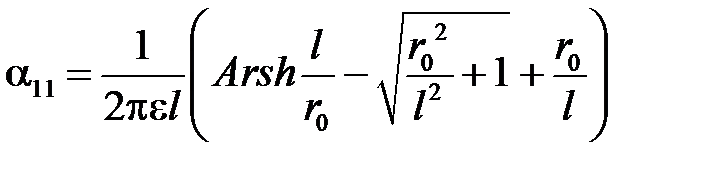Так как при выводе этой формулы наличие другого провода не учитывалось, то емкость уединенного цилиндра конечной длины получается из выражения

.

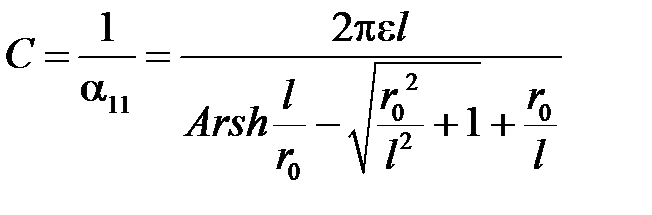Заметим, что имеет место соотношение

(*)

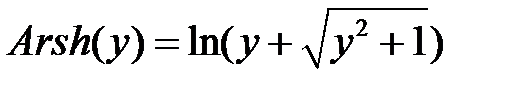С учетом (*) при 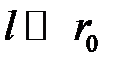будет

.

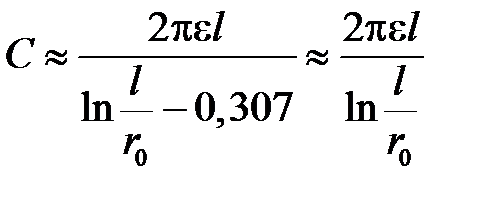Емкость между цилиндрами найдется:

,

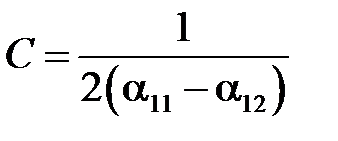где α₁₂ и α₁₁ находятся по только что полученным формулам.

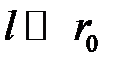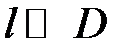При и имеем

.

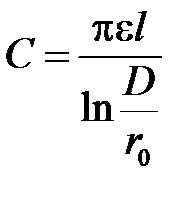Вопросы для самопроверки

1. Является ли электростатическое поле непрерывным?

2. Напишите уравнение, показывающее, что электрическое поле возникает в области, где расположен заряд. Дайте физическое толкование понятиям градиента и дивергенции.

3. Как изменяется напряженность электростатического поля при переходе из одной среды в другую?

4. Какие поля называют потенциальными?

6. Могут ли быть замкнутыми силовые линии в электростатическом поле?

7. Каким свойством обладает силовая трубка?

8. Изложите основные принципы графического построения картины поля?

Как по картине поля определить напряженность электрического поля? При решении каких задач целесообразно применять теоремуГаусса в интегральной форме?Какой радиус должен иметь уединенный металлический шар в воздухе, чтобы на нем можно было разместить заряд величиной 1 кулон? Пробивная напряженность воздуха 30 кВ/см.

9.

10. Какой физический смысл придается 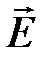и φ? Какая интегральная и дифференциальная связь существует между ними?

11. Определить модуль вектора напряженности электрического поля

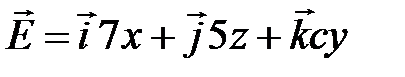,(В/м)

в точке с координатами x=2 (м), y=3 (м), z=4 (м).

13. Определить объемную плотность зарядовρ(мкКл/м3)

при потенциале: 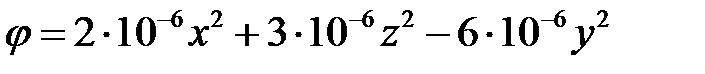,В.

2.