Граничное условие для номальной составляющей на поверхности раздела двух проводящих сред

Условия для векторов d и Е при переходе границы раздела проводящих сред получают так же, как условия для векторов электрического поля на границе раздела двух диэлектриков.

На границе раздела двух сред с различными проводимостями и вы­делим точку и окружим ее элементарным цилиндром, у которого высота бесконечно мала по сравнению с линейными размерами оснований (рис.1.8а).

Из Принцип непрерывности тока в интегральной форме аналогично предыдущему имеем или .

На границе раз­дела двух сред с различными проводимостями равны нормальные составляю­щие вектора плотности тока .

Для кастельных со­ставляющие вектора на­пряженности поля было получено ранеедля границы диэлектриков или .

На границе раздела двух сред с различными проводимостями и равны тангенциальные со­ставляющие вектора на­пряженности поля .

Получим соотношение, определяющее преломление векторов на границе проводящих сред сразличными свойствами:

.

Энергия электромагнитного поля.

Теорема Умова-Пойтинга

Плотность энергии электрического поля определяется

.

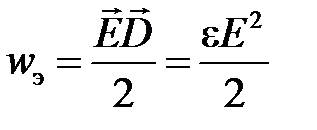Плотность энергии магнитного поля имеет вид .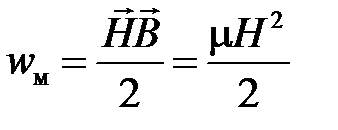

Плотность энергии электромагнитного поля может быть представлена как .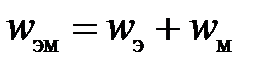

Энергия электромагнитного поля 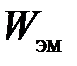в объеме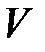

.

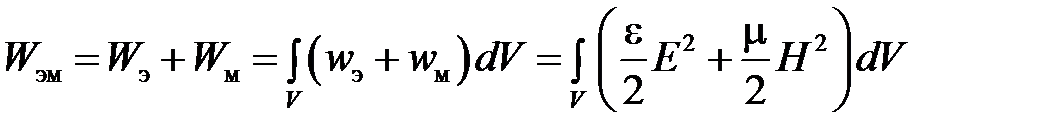Вектор Пойнтинга —вектор, равный векторному произведению напряженности электрического поля и напряженности магнитного поля, поток которого сквозь некоторую поверхность, представляет собой мгновенную электромагнитную мощность, передаваемую сквозь эту поверхность.

Вектор Пойнтинга 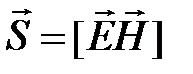характеризует величину и направление энергии, проходя­щей в единицу времени через единицу площади в на­правлении вектора Пойнтинга (рис.1.13).

Теорема Умова‒Пойтинга математически выражает закон сохранения энергии в электромагнитном поле.

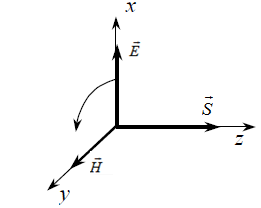
Рис.1.13. Вектор Пойнтинга

Выделим в переменном электромагнитном поле некоторый объем V, ограниченный поверхностью S. Внутри выделенного объема могут оказаться час­тично или полностью ис­точники и приемники электрической энергии в любых сочетаниях. Будем считать среду однородной и изотропной. Электромагнитное поле внутри объема описывается системой уравнений Максвелла:

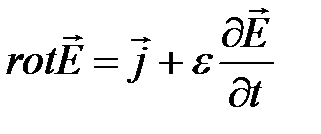, (1.8)

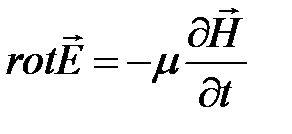, ( 1.9)

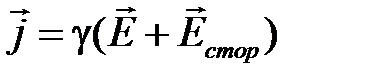. ( 1.10)

Здесь 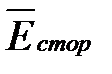— вектор стороннего электрического поля (внутри источников электрической энергии).

Умножим скалярно уравнение (1.8) на 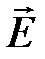а уравнение (1.9) на 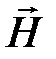, и вычтем почленно ле­вые и правые части уравнений:

.

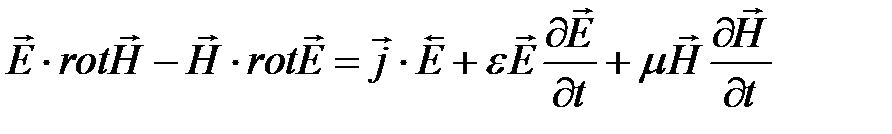Из курса математики известно, что

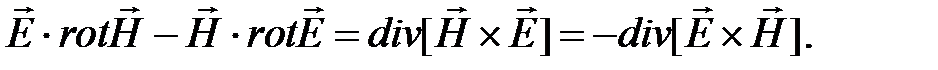
Преобразуем правые части уравнения. Из закона Ома (1.9) следует:

;

.

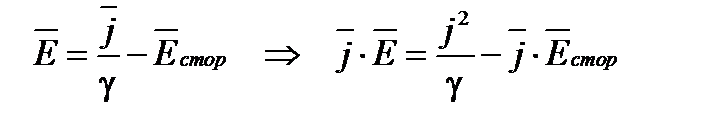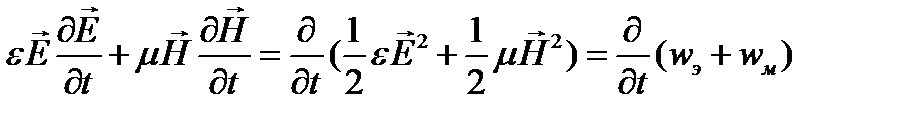После преобразования получим:

.

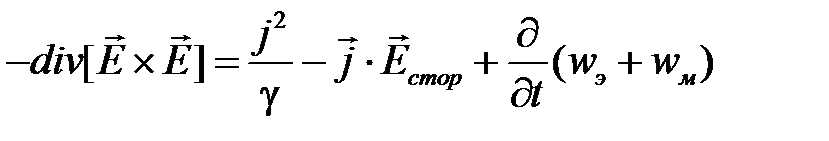Проинтегрируем все члены полученного уравнения по выделенному объ­ему V:

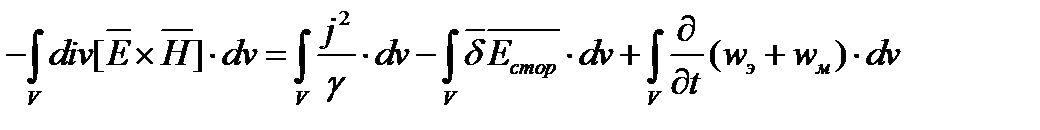
Преобразуем левую часть по теореме Остроградского -Гаусса:

.

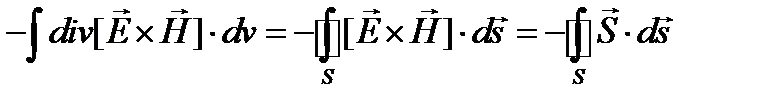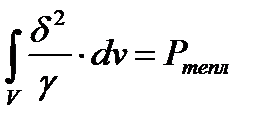— мощность тепловых потерь или потребляемая мощность в заданном объеме, эта мощность всегда положительна;

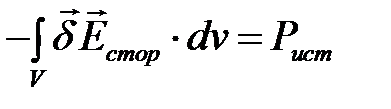— мощность источников энергии внутри объема, эта мощность от­рицательна, если векторы 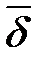и 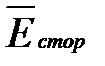совпадают, и положительна, если эти векторы не совпа­дают;

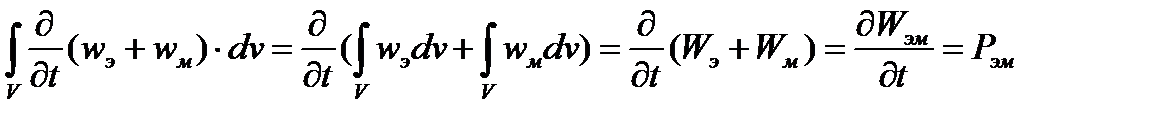— мощность элек­тро­магнитного поля в объеме — она положительна, если идет процесс накопления энергии в объеме, и от­рицательна, если идет процесс возврата энергии.

Таким образом, после принятых обозначений теорема Умова-Пойтинга получит вид:

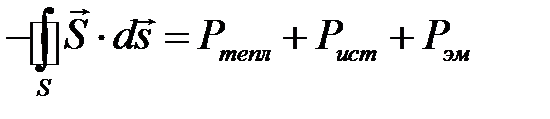
или

.

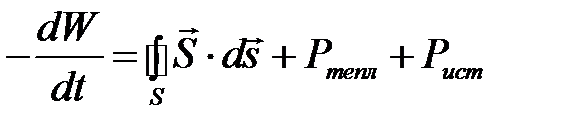Скорость изменения электромагнитной энергии, запасенной в объеме, равна сумме потока мощности через поверхность, ограничивающую этот объем, и мощности, поглощаемой или выделяемой протекающими в объеме токами.

Замечания.

1. В общем случае величина вектора Умова-Пойнтинга и дивергенция вектора Умова-Пойнтинга говорит только о наличии внутри выделенного объема электрических и магнитных полей. Наличие или отсутствие излучения показывает не дивергенция вектора Умова-Пойнтига, а только баланс энергии, согласно общему закону сохранения энергии.

2. Физический смысл «потока вектора Умова-Пойнтинга» в общем виде не определяет наличие излучения или поглощения электромагнитной энергии. Физический смысл имеет только поток вектора Умова-Пойнтинга в случае если магнитный поток В,входящий в уравнение Умова-Пойнтинга, создан в результате электрических токов при движении электрических зарядов под действием электрического поля, также входящего в то же самое уравнение. Другими словами, если магнитное поле существует независимо от внешнего электрического поля (например, для постоянных магнитов), то в этом случае теорема Умова-Пойнтинга недействительна. И поток вектора Умова-Пойнтинга в этом случае ничего не определяет, кроме наличия в выделенном объеме совместно отдельного электрического поля и отдельного магнитного поля.