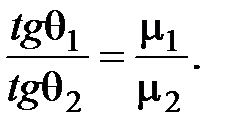Закон электромагнитной индукции

В интегральной форме.

Электродвижущая сила, возникающая в контуре при изменении магнитного потока сквозь поверхность, ограниченную этим контуром, равна скорости изменения потока, взятой со знаком "минус", т.е. (рис.1.6).

Рис.1.6. Контур в переменном магнитном поле

С учетом, что э.д.с. 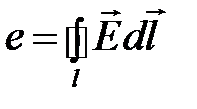и магнитный поток 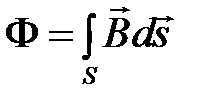закон можно представить в форме

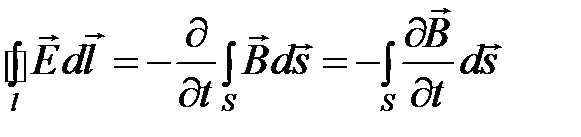. (1.2)

Левая часть уравнения (1.2) преобразуем по теореме Стокса:

.

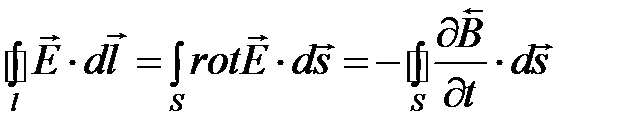Отсюда имеем дифференциальную форму закона электромагнитной индукции

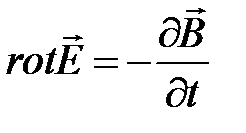или .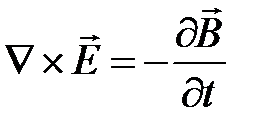

Из закона электромагнитной индукции следует, что любое изменение магнитного поля во времени вызывает возникновение в той же точке пространства связанного с ним поля электрического.

В декартовой системе координат операция записыватся так:

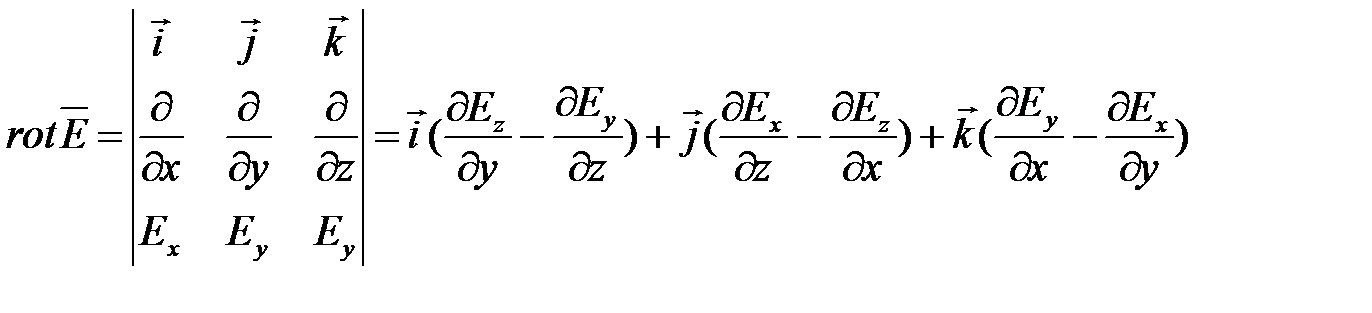
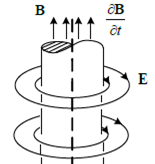
Рис.1.7. Магнитопровод с переменным магнитным потоком

На рис.1.7 изображено электрическое поле (концентрические окружности), обусловленное изменением магнитной индукции внутри ферромагнитного стержня. Как видно, линии вектора 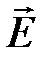охватывают линии вектора 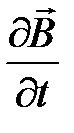и образуют с ним левовинтовую систему.

Принцип непрерывности магнитной индукции

Поток вектора магнитной индукции сквозь любую замкнутую поверхность равен нулю:

. (1.3)

Перейдем к дифференциальной форме записи уравнения (1.3), используя теорему Остроградского–Гаусса:

.

Отсюда имем принцип непрерывности магнитной индукции в дифференциальной форме:

или . (1.4)

В декартовой системе координат уравнение (1.4) записывается

.

1.2.4. Теорема Гаусса (постулат Максвелла)

В интегральной форме.

Поток вектора электрической индукции (вектора электрического смещения) сквозь произвольную замкнутую поверхность равен алгебраической сумме свободных зарядов, расположенных в объеме, ограниченном этой поверхностью (рис. 1.8):

, (1.5)

Рис.1.8. Электрическое поле объёмного заряда

Теорему Гаусса Максвелл обобщил (постулировал) и на переменные электрические поля.

Левую часть уравнения (1.5) преобразуем по теореме Остроградского‒Гаусса:

.

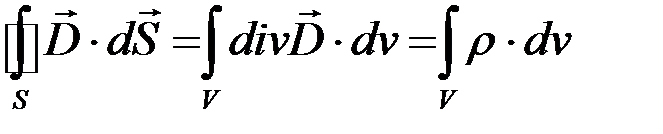Отсюда имеем теорему Гаусса в дифференциальной форме:

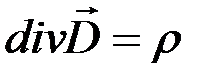. (1.6)

В декартовой системе координат уравнение (1.6) записывается

.

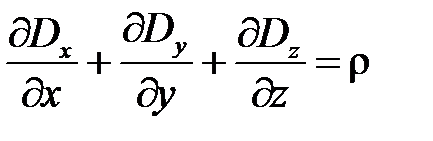Система уравнений Максвелла

Система уравнений Максвелла, наиболее полно и точно (насколько это известно) описывает все проявления электромагнитного поля.

, , , .

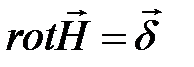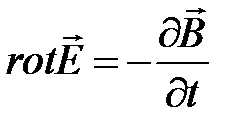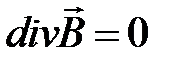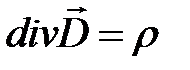Материальные уравне­ния:

, , .

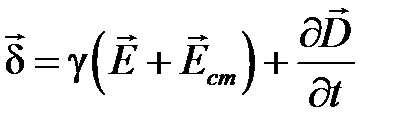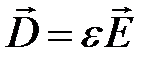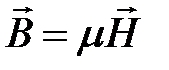Здесь 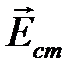― вектор стороннего электрического поля (внутри источников электрической энергии).

Уравнения в Максвелла, записанные в дифференциальной форме в выбранной системе координат, справедливы для областей, в которых вектора поля 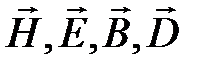непрерывны и дифференцируемы. На границе раздела сред с различными электрическими и магнитными свойствами, а также в точках поверхностей с распределениями на них поверхностных зарядов или тонких слоев токов, эти векторы терпят разрыв и их производные не существуют. На границе раздела сред дифференциальные уравнения теряют свой смысл. Для нахождения электромагнитного поля нужно добавить соотношениями, связывающими составляющие векторов 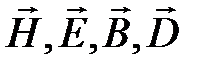по обе стороны поверхностей раздела сред. иназываемыми граничными условиями. Взаимосвязи между значе,ниями составляющих векторов в разных средах у поверхности раздела называют граничными условиями. Для получения граничных условий нужно использовать уравнения Максвелла в интегральной форме.

1.3.2.Граничные условия для векторов магнитного поля

Граничное условие для нормальных составляющих вектора индукции магнитного поля при переходе границы раздела с магнитными проницаемостям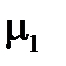и и 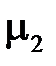выводятся так же, как для нормальных составляющих вектора электрического смещения.

Рассмотрим элементарный цилиндр, охватывающий точку на поверхности раздела сред с 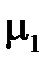и 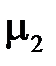, (рис. 1.11).

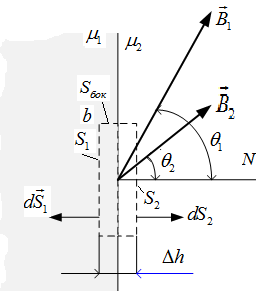
Рис.1.11. Векторы индукции магнитногоо поля на границе сред

Принцип непрерывности магнитного потока в интегральной форме 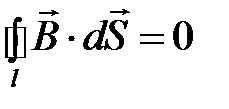, записанный для поверхности цилиндра, после интегрирования и преобразований приводит к уравнению

.

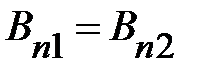На поверхности раздела равны нормальные составляющие вектора индукции магнитного поля.

Граничное условие для касательных составляющих вектора напряженности магнитного поля.

Для элементарного контура abcd (рис. 1.ё12), охватывающего точку на границе сред с 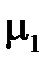и 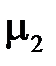применим закон полного тока в интегральной форме:

.

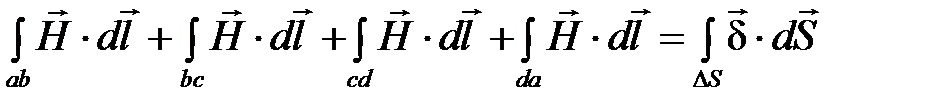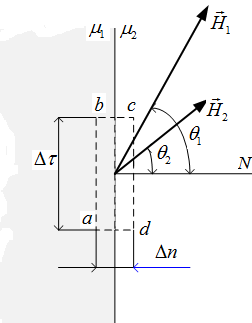
Рис.1.12

Пусть размеры сторон контура удовлетворяют условию .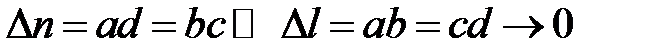

Пренебрегая вкладом в интеграл на боковых сторонах bc и da ввиду их малости и учитывая, что 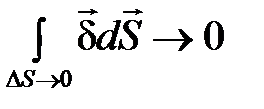, имеем:

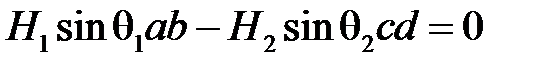
Принимая во внимание, что ab = cd, получаем H₁sinq₁ = H₂sinq₂ или

.

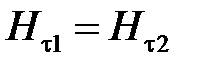На поверхности раздела равны касательные составляющие вектора напряженности магнитного поля.

Из условий на поверхности раздела для векторов 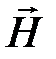и 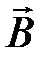получаем соотношение, определяющее преломление векторов на границе сред сразличными магнитными свойствами:

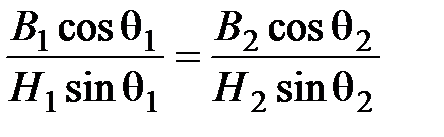или