Общие сведения теории электромагнитного поля
Солнышкин Н.И.
ТЕОРЕТИЧЕСКИЕ
ОСНОВЫ ЭЛЕКТРОТЕХНИКИ
Часть III
ОСНОВЫ ТЕОРИИ
ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
Псков
Псковский государственный университ
УДК 621.3.01 (075.8)
Солнышкин Н.И.
Теоретические основы электротехники. Часть 3. Теория электромагнитного поля: Учебное пособие. ―Псков: Псковский государственный университет, 2017. 50 с.
В пособии рассматриваются основные понятия и законы теории электромагнитного поля. Приводятся конкретные примеры, поясняющие излагаемый теоретический материал. Приводятся решения задач расчета электрических и магнитных полей.
Пособие предназначено для самостоятельной работы студентов-бакалавров электротехнических и электроэнергетических направлений всех форм обучения факультета вычислительной техники и электроэнергетики.
УДК 621.3.01 (075.8)
Солнышкин Н.И.
Ó Псковский государственный университет, 2017
Оглавление
Оглавление 3
Введение 6
1. Общие сведения теории электромагнитного поля 6
1.1. Векторные величины, 7
характеризующие электромагнитное поле 7
1.2. Уравнения Максвелла 10
1.2.1. Закон полного тока 10
1.2.2. Закон электромагнитной индукции 12
1.2.3. Принцип непрерывности магнитной индукции 14
1.2.4. Теорема Гаусса (постулат Максвелла) 14
1.2.5. Система уравнений Максвелла 15
1.3.2.Граничные условия для векторов магнитного поля 15
1.4.3. Граничное условие для номальной составляющей на поверхности раздела двух проводящих сред 17
1.5. Энергия электромагнитного поля. 18
Теорема Умова-Пойтинга 18
1.6. Частные виды электромагнитных полей 21
2. Электростатическое поле 22
2.1. Уравнения электростатического поля 22
2.2. Электрический потенциал 22
2.3. Потенциал заданного распределения заряда 23
2.4. Уравнение Пуассона и Лапласа 24
2.5. Граничные условия для векторов электрического поля 25
2.6. Теорема единственности решения 28
2.7. Электростатическое экранирование 28
2.8. Энергия электростатического поля 29
2.9. Плоскопараллельное электростатическое поле. 30
Функция потока. Картина поля 30
2.10. Расчёт электростатических полей 32
2.10.1. Графический метод построения картины 32
плоскопараллельного поля 32
2.10.2. Расчёт поля плоского конденсатора при наличии между 33
обкладками свободных зарядов 33
2.10.3. Поле линейного заряда и поле кругового 35
проводящего цилиндра 35
2.10.4. Поле и емкость цилиндрического конденсатора 36
2.10.5. Поле двух параллельных разноименно заряженных осей 37
2.10.6. Электростатическое поле и емкость разноименно заряженных параллельных цилиндров. Поле двухпроводной линии 39
2.10.7. Метод зеркальных изображений. Поле заряженной оси, расположенной вблизи плоской границы раздела двух диэлектриков 41
Рассмотрим поле оси, расположенной на расстоянии h от границы раздела двух диэлектриков с диэлектрическими проницаемостями e1 и e2 (рис.2.15а). 41
Поле заряженной оси, 43
расположенной вблизи проводящей плоскости 43
2.10.9. Потенциальные коэффициенты,коэффициенты 44
электростатической индукции и частичные ёмкости 44
системы проводников 44
2.10.10. Поле и ёмкость двухпроводной линии с учетом влияния земли 45
2.10.11. Электрическое поле и ёмкость трехфазной линии 48
2.11. Метод средних потенциалов для расчёта потенциальных коэффициентов и ёмкостей в системе проводов 50
Вопросы для самопроверки 53
Электрическое поле постоянного тока 53
3.1. Электрическое поле в диэлектрике, окружающем 54
проводники с постоянными токами 54
3.2.Электрическое поле постоянного тока в проводящей среде 55
3.2.1. Уравнения электрического поля постоянного тока 55
3.2.2. Граничные условия на поверхности раздела 56
двух проводящих сред 56
3.2.3. Метод электростатической аналогии 57
3.2.4. Расчёт тока утечки коаксиального кабеля 58
3.2.5. Заземлитель в виде шара 59
Вопросы для самопроверки 61
4. Магнитное поле постоянных токов 61
4.1. Уравнения магнитного поля дифференциальной форме 61
4. 2. Векторный потенциал магнитного поля 61
4.3. Выражение магнитного потока и энергии 63
через векторный потенциал 63
4.4.Граничные условия в магнитном поле 65
4.5. Скалярный потенциал магнитного поля 66
4.6.Плоскопараллельное магнитное поле 67
4.7.Магнитное поле и внутренняя индуктивность прямого провода 69
4.8.Соответствия электростатического (электрического) поля и магнитного поля постоянного тока 71
4.9. Поток вектора Пойтинга в коаксиальном кабеле 73
4.10. Магнитное поле и индуктивность двухпроводной линии 74
4.11.Общие выражения для взаимной и собственной индуктивностей контуров из линейных проводников 76
4.12.Метод участков расчёта индуктивностей 77
4.13. Индуктивности контуров, составленных из прямолирейных участков 79
4.14.Индуктивность трехфазной линии 80
4.15. Графический метод построения картины плоскопараллельногомагнитногополя поля 82
4.16.Поле токов вблизи плоских поверхностей ферромагнитных тел. Метод зеркальных изображений 84
4.17.Магнитное экранирование 85
Вопросы для самопроверки 86
5. Переменное электромагнитное поле 86
5.1.Уравнения Максвелла в комплексной форме 86
5.2. Плоская гармоническая волна в диэлектрике 87
5.3. Плоская гармоническая волна в проводящей среде 89
5.4. Магнитный поверхностный эффект в плоском листе 91
5.5.Электрический поверхностный эффект в плоской шине 94
5.6.Эффект близости 96
5.7. Поверхностный эффект в круглом проводе 98
5.8. Экранирование в переменном магнитном поле 102
Вопросы для самопроверки 103
Приложение 1. 104
Выражения градиента, дивергенции, ротора и лапласиана в различных системах координат 104
Литература 105
Оглавление 3
Введение 6
1. Общие сведения теории электромагнитного поля 6
1.1. Векторные величины, 7
характеризующие электромагнитное поле 7
1.2. Электрический ток. Виды плотности тока 8
1.3. Уравнения Максвелла 9
1.3.1.Закон полного тока 9
3.2. Закон электромагнитной индукции 10
1.3.3. Принцип непрерывности магнитной индукции 11
1.3.4. Теорема Гаусса (постулат Максвелла) 12
1.3.5. Система уравнений Максвелла 13
1.4.Граничные условия 13
1.4.1.Граничныеусловия для векторов электрического поля 13
1.4.2.Граничные условия для векторов магнитного поля 15
1.4.3.Граничные условия на поверхности раздела 17
двух проводящих сред 17
1.5.Энергия электромагнитного поля. 18
Теорема Умова-Пойтинга 18
1.6.Частные виды электромагнитных полей 20
2.Электростатическое поле 20
2.1.Уравнения электростатического поля 21
2.2. Электрический потенциал 21
2.3.Потенциал заданного распределения заряда 22
2.4.Уравнение Пуассона и Лапласа 22
2.5. Граничные условия для векторов электрического поля 23
2.6.Теорема единственности решения 24
2.7. Проводники в электростатическом поле. Электростатическое экранирование 24
2.8. Энергия электростатического поля 25
2.9. Плоскопараллельное электростатическое поле. 26
Функция потока. Картина поля 26
2.10.Расчёт электростатических полей 28
2.10.1. Графический метод построения картины 28
плоскопараллельного поля 28
2.10.2.Расчёт поля плоского конденсатора при наличии свободных зарядов 29
2.10.3. Поле линейного заряда и поле кругового проводящего цилиндра 31
2.10.4.Поле и емкость цилиндрического конденсатора 32
2.10.5. Поле двух параллельных разноименно заряженных осей 33
2.10.6.Электростатическое поле и емкость разноименно заряженных параллельных цилиндров. Поле двухпроводной линии 35
2.10.7. Метод зеркальных изображений. Поле заряженной оси, расположенной вблизи плоской границы раздела двух диэлектриков 37
2.10.8.Поле заряженной оси, 39
расположенной вблизи проводящей плоскости 39
2.10.9. Потенциальные коэффициенты,коэффициенты 40
электростатической индукции и частичные емкости 40
системы проводников 40
2.10.10.Поле и емкость двухпроводной линии с учетом влияния земли 41
2.10.11. Электрическое поле и емкость трехфазной линии 44
2.11. Метод средних потенциалов для расчёта потенциальных коэффициентов и емкостей в системе проводов 46
3. Электрическое поле постоянного тока 49
3.1. Электрическое поле в диэлектрике, окружающем 49
проводники с постоянными токами 49
3.2.Электрическое поле постоянного тока в проводящей среде 50
3.2.1. Уравнения электрического поля постоянного тока 50
3.2.2.Граничные условия на поверхности раздела 50
двух проводящих сред 50
3.2.3. Метод электростатической аналогии 51
3.2.4. Расчёт тока утечки коаксиального кабеля 52
3.2.5. Заземлитель в виде шара 53
4. Магнитное поле постоянных токов 54
4.1. Уравнения магнитного поля дифференциальной форме 55
4. 2. Векторный потенциал магнитного поля 55
4.3. Выражение магнитного потока и энергии 57
через векторный потенциал 57
4.4. Граничные условия в магнитном поле 58
4.5. Скалярный потенциал магнитного поля 58
4.6. Плоскопараллельное магнитное поле 60
4.7. Магнитное поле и внутренняя индуктивность прямого провода 61
4.8. Соответствия электростатического (электрического) поля и магнитного поля постоянного тока 64
4.9. Поток вектора Пойтинга в коаксиальном кабеле 65
4.10. Магнитное поле и индуктивность двухпроводной линии 67
4.11. Общие выражения для взаимной и собственной индуктивностей контуров из линейных проводников 68
4.12. Метод участков расчёта индуктивностей 69
4.13. Индуктивности контуров, составленных из прямолирейных участков 71
4.14. Индуктивность трехфазной линии 72
4.15. Графический метод построения картины поля 74
4.16. Поле токов вблизи плоских поверхностей ферромагнитных тел. Метод зеркальных изображений 76
4.17. Магнитное экранирование 77
Вопросы для самопроверки 78
5. Переменное электромагнитное поле 78
5.1. Уравнения Максвелла в комплексной форме 78
5.2. Плоская гармоническая волна в диэлектрике 79
5.3. Плоская гармоническая волна в проводящей среде 81
5.4. Магнитный поверхностный эффект в плоском листе 83
5.5. Электрический поверхностный эффект в плоской шине 86
5.6. Эффект близости 88
5.7. Поверхностный эффект в круглом проводе 90
5.8. Экранирование в переменном магнитном поле 94
Вопросы для самопроверки 95
Выражения градиента, дивергенции, ротора и лапласиана в различных системах координат 96
Литература 97
Введение
Основной задачей изучения дисциплины «Теория электромагнитного поля» является изучение одной из форм материи — электромагнитного поля и его проявлений в различных устройствах техники, усвоение современных методов моделирования электромагнитных процессов, методов анализа и расчёта электрических и магнитных полей, знание которых необходимо для понимания и успешного решения инженерных проблем будущей специальности.
Содержанием дисциплины является макроскопическая теория электромагнитного поля, основу теории, которой составляют сформулированные Максвеллом уравнения электродинамики.
Существует много важных практических случаев, когда анализ электромагнитных явлений может быть произведен только путём детального изучения электромагнитного поля. В качестве примеров можно указать на задачи в технике высоких напряжений, задачи о поверхностных эффектах, об излучении и распространении электромагнитных волн.
Расчёты электромагнитных полей являются основой для проектирования электромагнитных устройств и исследования процессов в них.
В пособии представлен материал третьей части курса «Теоретические основы электротехники», который охватывает следующие темы: уравнения электромагнитного поля, электростатическое поле, расчёт электрической ёмкости, электромагнитное поле постоянных токов, расчёт индуктивностей, переменное электромагнитное поле в диэлектрике, переменное электромагнитное поле в проводящей среде.
Векторные величины,
Векторы электрического поля
Для описания электрического поля используют векторы: вектор напряжённости электрического поля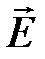 
,вектор поляризации 
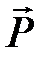, вектор электрического смещения (электрической индукции) 
.
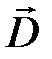1. Напряжённость электрического поля — физическая характеристика электрического поля, определяющая силовое воздействие поля на неподвижный электрический заряд.
Напряжённость электрического поля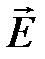 
является векторной величиной, численно равной отношению силы 
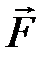, с которой электрическое поле действует на положительный заряд q, внесенный в рассматриваемую точку поля, к значению этого заряда, когда величина заряда стремится к нулю
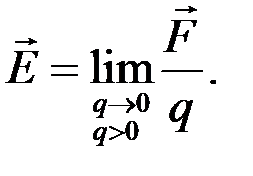
Сила взаимодействия зарядов, а следовательно, и напряжённость
электрического поля в различных средах различны. Это объясняется
поляризацией вещества ― ориентацией диполей относительно векторов поля (Рис. 1.1).
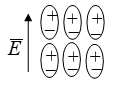
Рис. 1.1. Поляризация вещества
Поляризация характеризуется поляризованностью.
Поляризованность – это сумма всех дипольных моментов вещества, отнесенная к единице объема
Из-за поляризациидиэлектрика напряжённость электрического поля в диэлектрике уменьшается.
При несильных внешних электрических полях вектор поляризованности можно считать пропорциональным напряженности электрического поля
,
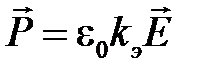где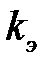 
— относительная диэлектрическая восприимчивость вещества;
ε0 — электрическая постоянная, равная 8,859·10–12 Ф/м.
Для характеристики электрического поля используется также вектор электрического смещения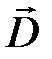 
, позволяющий исключить из рассмотрения свойства среды.
Вектор электрического смещения ― векторная величина, равная геометрической сумме вектора напряженности электрического поля в рассматриваемой точке, умноженной на электрическую постоянную, и вектора поляризованности в той же точке
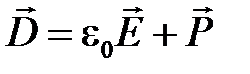
или
.
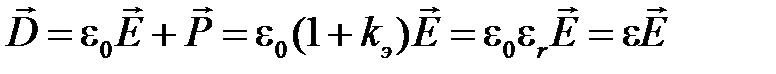Здесь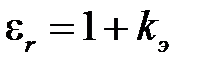 
― относительная диэлектрическая проницаемость среды;
ε ― абсолютная диэлектрическая проницаемость среды.
Векторы магнитного поля
Магнитное поле характеризуется векторами: магнитной индукцией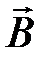 
, вектором намагниченности вещества 
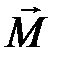, и вектором напряжённости магнитного поля 
.
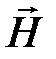Магнитная индукция ― векторная величина, характеризующая магнитное поле и определяющая силу, действующую на движущуюся электрически заряженную частицу со стороны магнитного поля.
Сила, действующая на движущийся заряд равна:
.
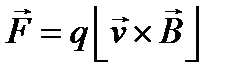Здесь q ― электрический заряд; v ― скорость.
Направление силы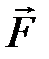 
находят по правилу векторного произведения (рис.1.2).
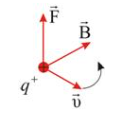
Рис. 1.2. Сила Лоренца
Сила 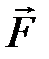максимальна, если вектор скорости 
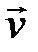перпендикулярен вектору индукции 
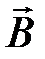.В этом случае
.
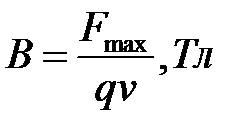Итак, магнитная индукция равна отношению силы, действующей на электрически заряженную частицу, к произведению заряда и скорости частицы, если направление скорости таково, что эта сила максимальна, и имеет направление, перпендикулярное к векторам силы и скорости, совпадающее с поступательным перемещением правого винта при вращении его от направления силы к направлению скорости частицы с положительным зарядом.
Магнитное поле действует, не только на отдельные движущиеся
заряды, но и на проводники, по которым течет электрический ток (рис.1.3).
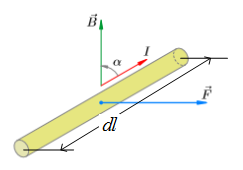
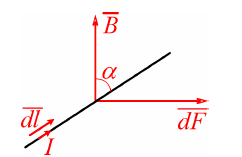
Рис.1.3. Проводник с током в магнитном поле
Например, сила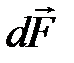 
, с которой однородное магнитное поле действует на элемент dl тонкого проводника с токм I равна
,
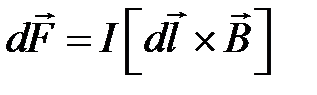где вектор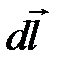 
направлен понаправлению тока в проводнике.
Направление силы d F → {\displaystyle d{\vec {F}}} определяется по правилу вычисления векторного произведения, которое удобно запомнить при помощи правила левой руки. Модуль силы Ампера можно найти по формуле:
d F = I B d l sin α , {\displaystyle dF=IBdl\sin \alpha ,}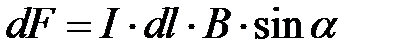 
,
где α {\displaystyle \alpha }a — угол между вектором магнитной индукции и направлением, вдоль которого течёт ток.
Полная сила F , действующая на проводник длиной l с током I, составит
.
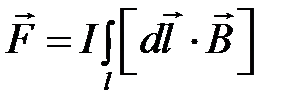Если проводник прямолинейный, а индукция B на оси проводника по-
стоянна и перпендикулярна направлению тока I, то модуль вектора си-
лы может быть рассчитан следующим образом
/
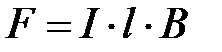
Направление силы d F → {\displaystyle d{\vec {F}}} определяется по правилу вычисления векторного произведения, которое удобно запомнить при помощи правила левой руки. Модуль силы Ампера можно найти по формуле:
d F = I B d l sin α , {\displaystyle dF=IBdl\sin \alpha ,}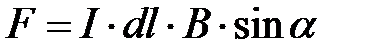 
,
где α {\displaystyle \alpha }a — угол между вектором магнитной индукции и направлением, вдоль которого течёт ток.
Величина индукции зависит от свойств среды. Под действием магнитного поля вещество может намагничиваеться. В этом случае появляется дополнительное поле, которое налагается на первичное поле. Намагничивание характеризуется намагниченностью.
Намагниченность ( 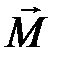) ―векторная величина, равная сумме магнитных моментов атомов в единице объема вещества: 
.
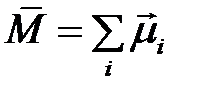Вектор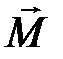 
измеряется в амперах на метр (А/м).
При рассмотрении многих процессов удобно ввести вектор напряженности магнитного поля.
Напряжённость магнитного поля ― векторная величина, равная геометрической разности магнитной индукции, деленной на магнитную постоянную, и намагниченности.
.
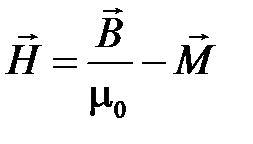Намагниченность связана с 
соотношением:
,
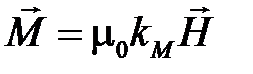где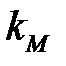 
― магнитная восприимчивость, характеризует свойство вещества намагничиваться в магнитном поле.
С вектором магнитной индукции напряжённость магнитного поля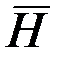 
связана соотношением:
,
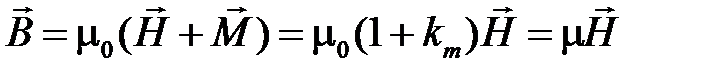где μ = μ0 μr ― абсолютная магнитная проницаемость;
μ0 = 4π∙10-7 Гн/м ― магнитная постоянная;
μr ― относительная магнитная проницаемость.
Уравнения Максвелла
Закон полного тока
В интегральной форме.
Циркуляция напряженности магнитного поля по любому замкнутому контуру равна полному току сквозь поверхность, ограниченную этим контуром (рис.1.4):
.
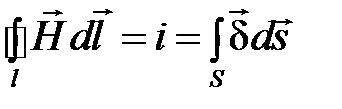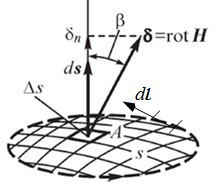
Рис. 1.4. Контур в магнитном поле
Левую часть уравнения преобразуем по теореме Стокса:
.
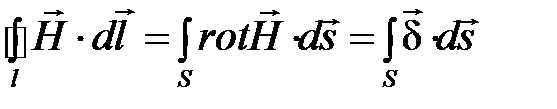Отсюда имеем дифференциальную форму закона полного тока:
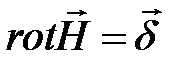или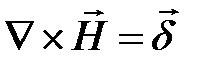 
, (1.1)
где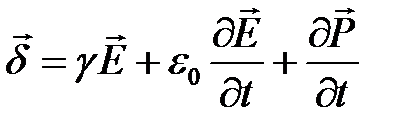 
― вектор плотности полного тока ;
―оператор пространственного дифференцирования ― оператор на́бла (оператор Гамильтона).
В декартовой системе координат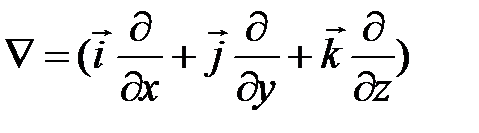 
и операция 
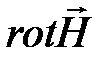записыватся так:
.
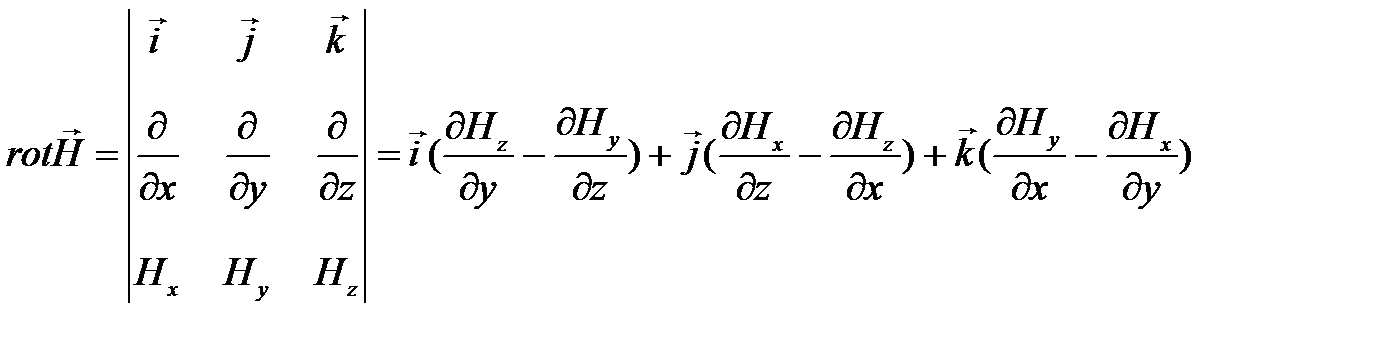Для наглядного представления о роторе вектора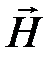 
на рис.1.3 изображены линии магнитного поля цилиндра с током плотностью δ. Эти линии ― концентрические окружности ― показывают, что поле вихревое.
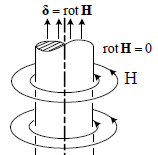
Рис.1.5. Цилиндрический проводник с током
.
Уравнение (1.1) представляет векторную запись трех уравнееий: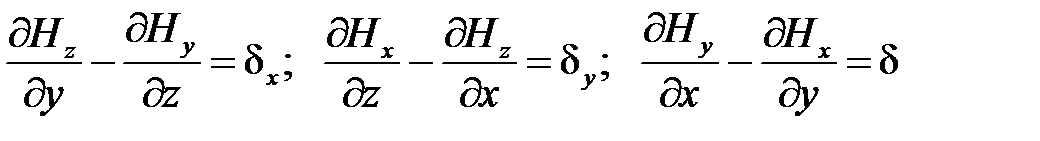 
.
Из закона полного тока видно, что магнитное поле порождается не только движущими зарядами (ток проводимости, ток переноса и ток поляризации), но и изменяющимся электрическим полем.
Возьмем операцию div от левой и правой части выражения закона полного тока:
.
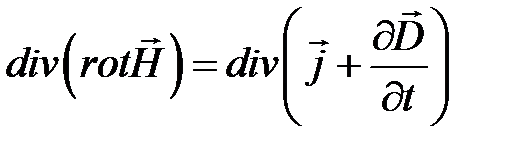Учитывая, что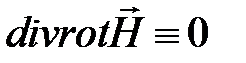 
, получаем
уравнение непрерывности плотности полного тока:
.
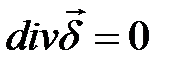Рис.1.6. Контур в переменном магнитном поле
С учетом, что э.д.с.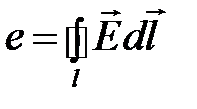 
и магнитный поток 
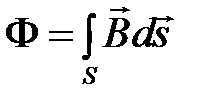закон можно представить в форме
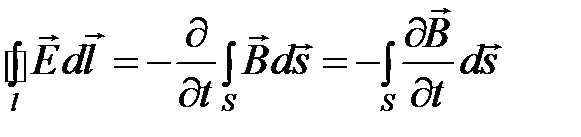. (1.2)
.
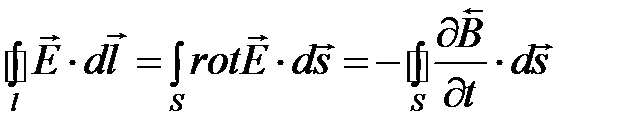Отсюда имеем дифференциальную форму закона электромагнитной индукции
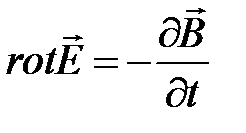или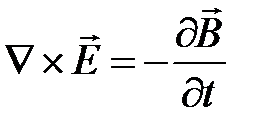 
.
Из закона электромагнитной индукции следует, что любое изменение магнитного поля во времени вызывает возникновение в той же точке пространства связанного с ним поля электрического.
В декартовой системе координат операция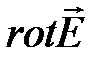 
записыватся так:
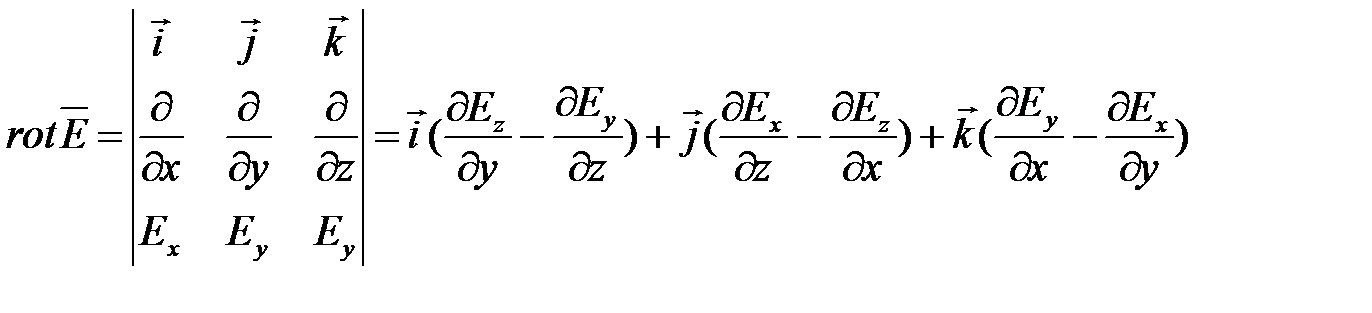
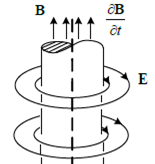
Рис.1.7. Магнитопровод с переменным магнитным потоком
На рис.1.7 изображено электрическое поле (концентрические окружности), обусловленное изменением магнитной индукции внутри ферромагнитного стержня. Как видно, линии вектора 
охватывают линии вектора 
и образуют с ним левовинтовую систему.
Рис.1.8. Электрическое поле объёмного заряда
Теорему Гаусса Максвелл обобщил (постулировал) и на переменные электрические поля.
Левую часть уравнения (1.5) преобразуем по теореме Остроградского‒Гаусса:
.
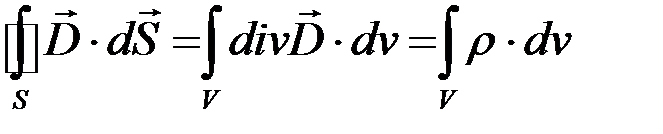Отсюда имеем теорему Гаусса в дифференциальной форме:
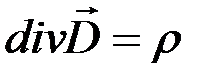. (1.6)
В декартовой системе координат уравнение (1.6) записывается
.
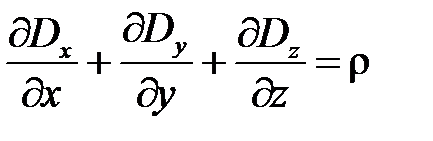Система уравнений Максвелла
Система уравнений Максвелла, наиболее полно и точно (насколько это известно) описывает все проявления электромагнитного поля.
, 
, 
, 
.
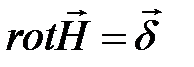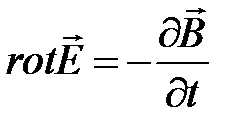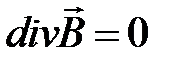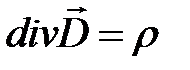Материальные уравнения:
, 
, 
.
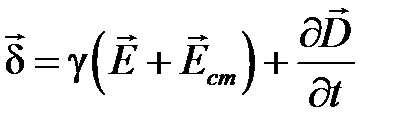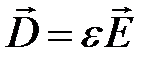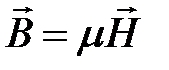Здесь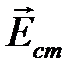 
― вектор стороннего электрического поля (внутри источников электрической энергии).
Уравнения в Максвелла, записанные в дифференциальной форме в выбранной системе координат, справедливы для областей, в которых вектора поля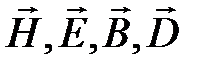 
непрерывны и дифференцируемы. На границе раздела сред с различными электрическими и магнитными свойствами, а также в точках поверхностей с распределениями на них поверхностных зарядов или тонких слоев токов, эти векторы терпят разрыв и их производные не существуют. На границе раздела сред дифференциальные уравнения теряют свой смысл. Для нахождения электромагнитного поля нужно добавить соотношениями, связывающими составляющие векторов 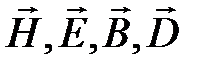по обе стороны поверхностей раздела сред. иназываемыми граничными условиями. Взаимосвязи между значе,ниями составляющих векторов в разных средах у поверхности раздела называют граничными условиями. Для получения граничных условий нужно использовать уравнения Максвелла в интегральной форме.
1.3.2.Граничные условия для векторов магнитного поля
Граничное условие для нормальных составляющих вектора индукции магнитного поля при переходе границы раздела с магнитными проницаемостям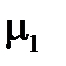и 
и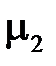 
выводятся так же, как для нормальных составляющих вектора электрического смещения.
Рассмотрим элементарный цилиндр, охватывающий точку на поверхности раздела сред с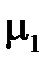 
и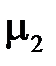 
, (рис. 1.11).
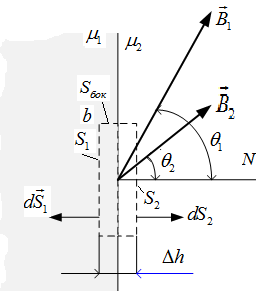
Рис.1.11. Векторы индукции магнитногоо поля на границе сред
Принцип непрерывности магнитного потока в интегральной форме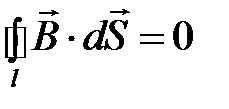 
, записанный для поверхности цилиндра, после интегрирования и преобразований приводит к уравнению
.
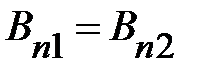На поверхности раздела равны нормальные составляющие вектора индукции магнитного поля.
Граничное условие для касательных составляющих вектора напряженности магнитного поля.
Для элементарного контура abcd (рис. 1.ё12), охватывающего точку на границе сред с 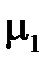и 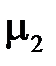применим закон полного тока в интегральной форме:
.
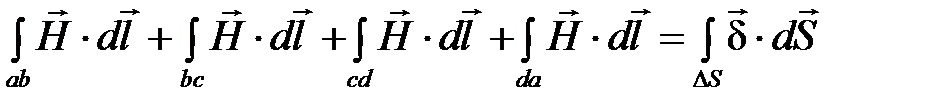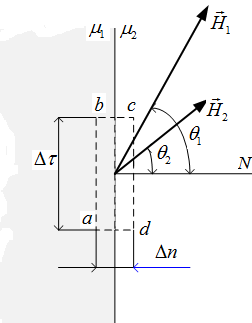
Рис.1.12
Пусть размеры сторон контура удовлетворяют условию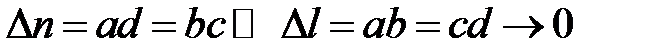 
.
Пренебрегая вкладом в интеграл на боковых сторонах bc и da ввиду их малости и учитывая, что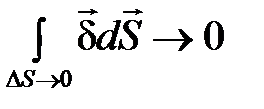 
, имеем:
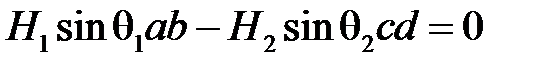
Принимая во внимание, что ab = cd, получаем H1sinq1 = H2sinq2 или
.
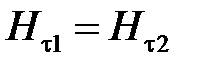На поверхности раздела равны касательные составляющие вектора напряженности магнитного поля.
Из условий на поверхности раздела для векторов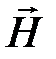 
и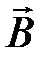 
получаем соотношение, определяющее преломление векторов на границе сред сразличными магнитными свойствами:
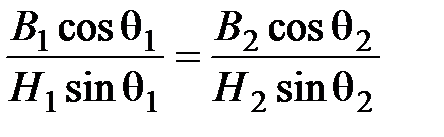или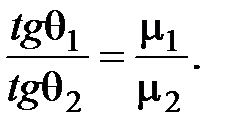 
Теорема Умова-Пойтинга
Плотность энергии электрического поля определяется
.
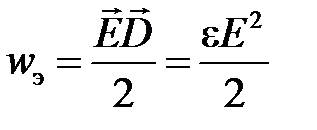Плотность энергии магнитного поля имеет вид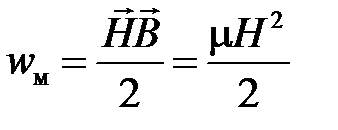 
.
Плотность энергии электромагнитного поля может быть представлена как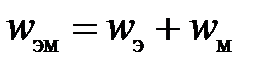 
.
Энергия электромагнитного поля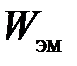 
в объеме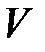 
.
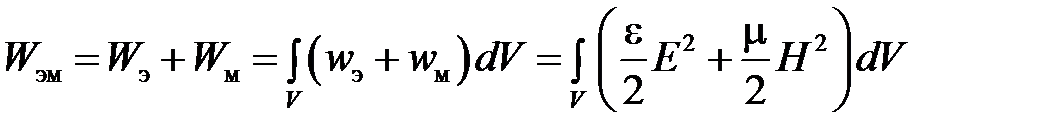Вектор Пойнтинга —вектор, равный векторному произведению напряженности электрического поля и напряженности магнитного поля, поток которого сквозь некоторую поверхность, представляет собой мгновенную электромагнитную мощность, передаваемую сквозь эту поверхность.
Вектор Пойнтинга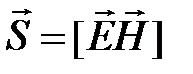 
характеризует величину и направление энергии, проходящей в единицу времени через единицу площади в направлении вектора Пойнтинга (рис.1.13).
Теорема Умова‒Пойтинга математически выражает закон сохранения энергии в электромагнитном поле.
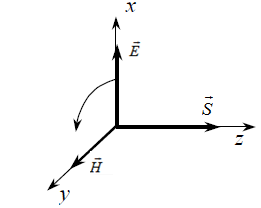
Рис.1.13. Вектор Пойнтинга
Выделим в переменном электромагнитном поле некоторый объем V, ограниченный поверхностью S. Внутри выделенного объема могут оказаться частично или полностью источники и приемники электрической энергии в любых сочетаниях. Будем считать среду однородной и изотропной. Электромагнитное поле внутри объема описывается системой уравнений Максвелла:
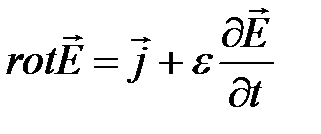, (1.8)
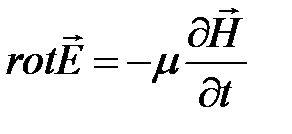, ( 1.9)
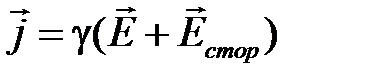. ( 1.10)
Здесь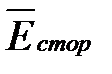 
— вектор стороннего электрического поля (внутри источников электрической энергии).
Умножим скалярно уравнение (1.8) на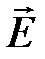 
а уравнение (1.9) на 
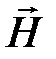, и вычтем почленно левые и правые части уравнений:
.
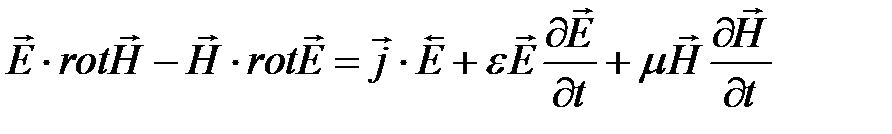Из курса математики известно, что
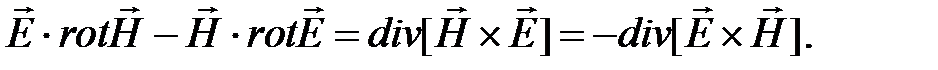
Преобразуем правые части уравнения. Из закона Ома (1.9) следует:
;
.
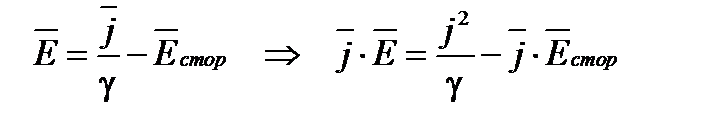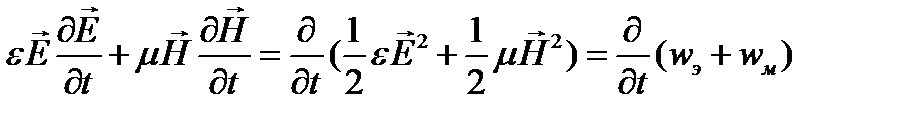После преобразования получим:
.
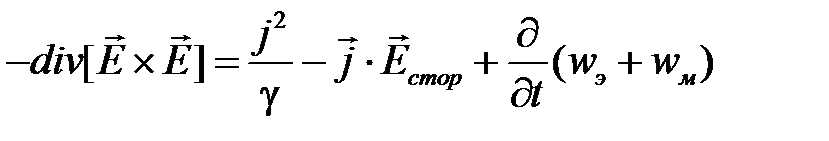Проинтегрируем все члены полученного уравнения по выделенному объему V: 
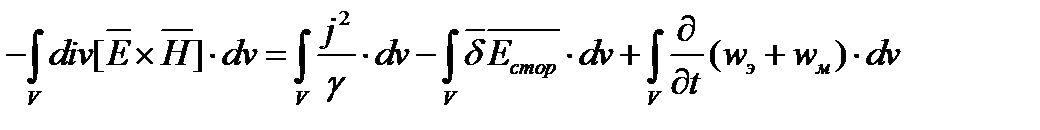
Преобразуем левую часть по теореме Остроградского -Гаусса:
.
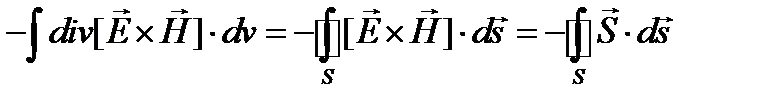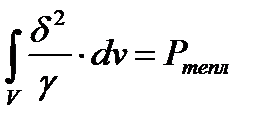— мощность тепловых потерь или потребляемая мощность в заданном объеме, эта мощность всегда положительна;
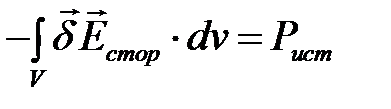— мощность источников энергии внутри объема, эта мощность отрицательна, если векторы 
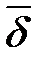и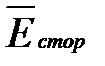 
совпадают, и положительна, если эти векторы не совпадают;
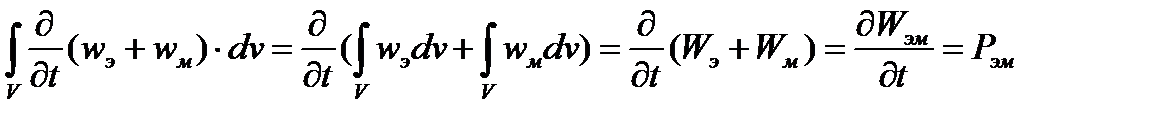— мощность электромагнитного поля в объеме — она положительна, если идет процесс накопления энергии в объеме, и отрицательна, если идет процесс возврата энергии.
Таким образом, после принятых обозначений теорема Умова-Пойтинга получит вид:
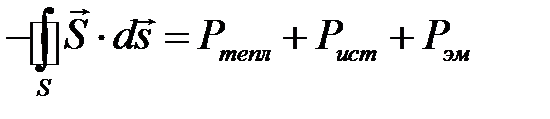
или
.
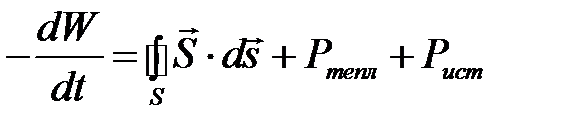Скорость изменения электромагнитной энергии, запасенной в объеме, равна сумме потока мощности через поверхность, ограничивающую этот объем, и мощности, поглощаемой или выделяемой протекающими в объеме токами.
Замечания.
1. В общем случае величина вектора Умова-Пойнтинга и дивергенция вектора Умова-Пойнтинга говорит только о наличии внутри выделенного объема электрических и магнитных полей. Наличие или отсутствие излучения показывает не дивергенция вектора Умова-Пойнтига, а только баланс энергии, согласно общему закону сохранения энергии.
2. Физический смысл «потока вектора Умова-Пойнтинга» в общем виде не определяет наличие излучения или поглощения электромагнитной энергии. Физический смысл имеет только поток вектора Умова-Пойнтинга в случае если магнитный поток В,входящий в уравнение Умова-Пойнтинга, создан в результате электрических токов при движении электрических зарядов под действием электрического поля, также входящего в то же самое уравнение. Другими словами, если магнитное поле существует независимо от внешнего электрического поля (например, для постоянных магнитов), то в этом случае теорема Умова-Пойнтинга недействительна. И поток вектора Умова-Пойнтинга в этом случае ничего не определяет, кроме наличия в выделенном объеме совместно отдельного электрического поля и отдельного магнитного поля.
Вопросы для самопроверки
1. Правильно ли понимать под электрическим током только движение заряженных частиц или тел? Является ли функция div D векторной?
2. Какие величины характеризуют электромагнитное поле?
3. Укажите размерности величин, характеризующих электромагнитное поле.
4. Какой формулой может выражаться индукция магнитного поля?
а) B=iB0e-αx ; б) B=iax+jby; в) B=iax ;г) B=iax-jby;
где: i, j-орты осей.
5. Под индукцией В,входящей в правую часть второго уравнения Максвелла следует понимать:
а)индукцию стороннего поля; б) индукцию индуцированного поля;
в) индукцию токов электрического смещения;
г) индукцию от тороннего и индуктированного полей.
6. Зависит ли входящий в правую часть уравнения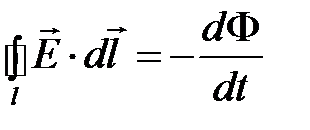 
магнитный поток от электрического тока, индуцированного этим током?
7. Каково значение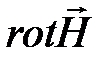 
в однородном магитном поле?
8. Какие отличия силовых линий магнитного поля от силовых линий поля электрического?
2. Каково значение величины rot Н в однородном магнитном поле?
9. При каких условиях справедливо выражение divH= 0?
10. Во всех точках некоторой области выполнено уравнение rotН=0. Может ли в этой области существовать магнитное поле?
11. Найти rotEв точке находящейся на расстоянии r0=0.2 м от линейного бесконечно длинного проводника с током i=14,1sin105t А. Проводник расположен в воздухе.
12. Определить плотность тока 
как функцию координат в области, где напряженность магнитного поля характеризуется функцией: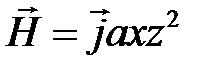 
,
a – постоянная.
Электростатическое поле
Поле электростатическое — электрическое поле неподвижных заряженных тел при отсутствии в них электрических токов.
Электрический потенциал
Для описания электростатического поля можно применять потенциальную функцию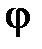 
называемую потенциалом.
Потенциал