Случай кривой, заданной явно.

Рассмотрим плоскую кривую, уравнение которой имеет вид

Если функция 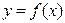является гладкой (т.е. непрерывно дифференцируемой) на 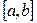, то длина дуги этой кривой вычисляется по формуле

.

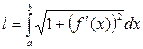Пример. Вычислить длину дуги параболы 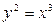, заключенной между точками (0,0) и (4,8).

Так как кривая задана неявно, то необходимо сначала выделить явно y относительно x, получим 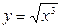. Отсюда 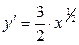. Абсцисса текущей точки параболы меняется в пределах от 0 до 4, т.е. 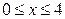, поэтому формула для вычисления длины дуги кривой примет вид

.

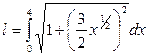Возьмем этот определенный интеграл

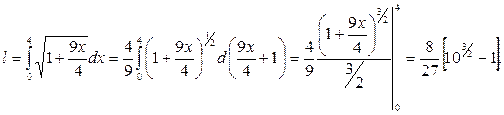
Случай кривой, заданной параметрически.

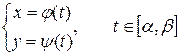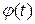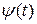Рассмотрим плоскую кривую, уравнение которой имеет вид , где функции и - непрерывно дифференцируемы на 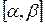, причем 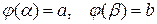. Тогда длина кривой вычисляется по формуле

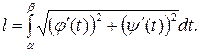
Пример. Найти длину одной арки циклоиды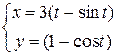

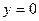
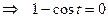
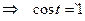
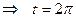
Найдем точки пересечения циклоиды с осью ОХ, для этого приравняем ординату y к нулю и решим уравнение 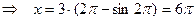. Следовательно, первой арке циклоиды соответствует изменение параметра в пределах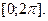

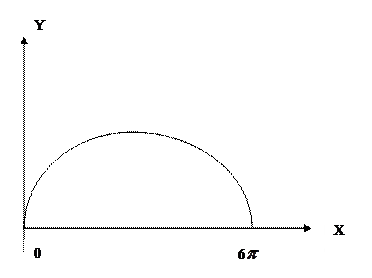
Найдем производные от абсциссы и ординаты этой кривой 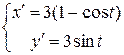. Используя формулу вычисления длины дуги для кривой, заданной параметрически, получим

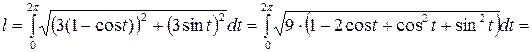
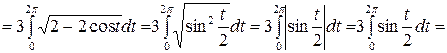
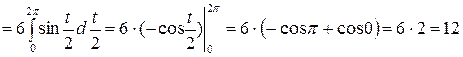
Случай кривой, заданной в полярных координатах.

Если гладкая кривая задана уравнением 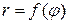в полярных координатах 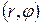, то длина дуги этой кривой определяется по формуле ,

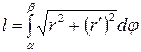где 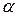и 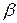- значения полярного угла в крайних точках дуги, причем .

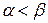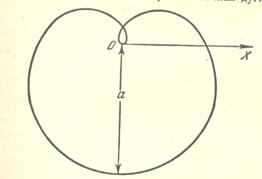
Пример. Найти длину кривой 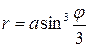. Текущая точка обойдет всю кривую, если полярный угол будет меняться в пределах

.

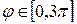Найдем производную функции

.

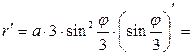
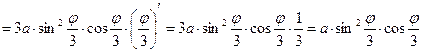Тогда подкоренное выражение примет вид:

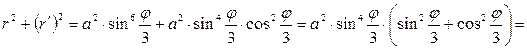
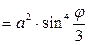
Для вычисления длины дуги кривой, заданной в полярных координатах, применим соответствующую формулу

.

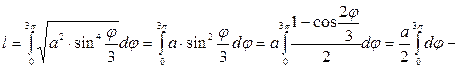
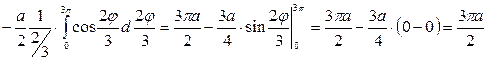Вычисление объема тела.

Формула объема тела по площади параллельных сечений.

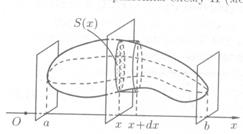
Пусть требуется найти объем тела V, причем известны площади S сечений этого тела, плоскостями, перпендикулярными координатным осям, например оси OX. Тогда площадь сечения является функцией от аргумента x: .

Искомая величина V находится путем интегрирования площади заданного сечения, т.е. .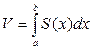

Пример. Найти объем сферы радиуса 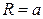с центром в начале координат О(0,0,0)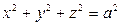

Рассмотрим сечение этой сферы плоскостью 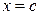, перпендикулярной оси ОХ, где 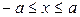. Для этого подставим в уравнение сферы вместо 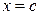и приведем полученное уравнение к каноническому виду:

.

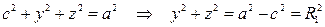Таким образом, сечения представляет собой новую окружность радиуса 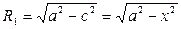с центром в точке 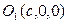. Используя формулу площади круга, известную из школьного курса 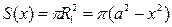. Используя формулу объема тела по площади параллельных сечений, получаем

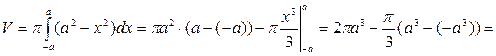
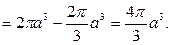
Объем тела вращения.

Пусть задана непрерывная кривая 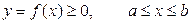. Рассмотрим фигуру, полученную вращением криволинейной трапеции 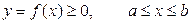вокруг оси ОХ. Фигура, полученная в результате вращения кривой вокруг любой из координатных осей, называется телом вращения .

Так как сечением тела вращения вокруг оси ОХ плоскостью 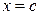является окружность радиуса 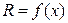, то площадь этого сечения будет равна .

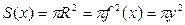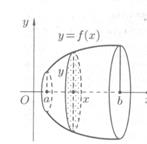Для нахождения объема тела вращения применим формулу объема тела по площади параллельных сечений:

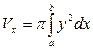
Если та же кривая вращается вокруг оси OY, то необходимо найти функцию, обратную к заданной и в качестве интервала интегрирования рассмотреть область значения исходной функции, т.е. . Тогда формула объема тела вращения вокруг оси OY примет вид: .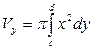

Пример 1. Найти объем тела, образованного вращением фигуры, ограниченной линиями 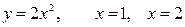, вокруг оси ОХ.

Применяя соответствующую формулу, получим

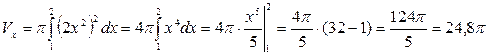
Пример 2. В условиях предыдущего примера найти объем тела вращения той же кривой вокруг оси OY.

Рассмотрим ту ветвь параболы, которая располагается в первой координатной четверти, и найдем функцию, обратную к заданной . Для этого выразим 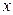через 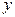. Искомая функцию будет иметь вид 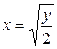, при этом, если x изменялся в пределах от 1 до 2, то y будет принимать значения из промежутка [2,8].

Тогда, используя формулу для вычисления объема тела вращения вокруг оси OY, получим:

.
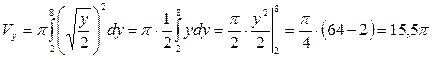