Явления переноса.диффузия.коэффициент диффузии.закон фика.

1)В результате хаотического движения молекул и соударений между ними происходят непрерывные изменения их скоростей и энергий в веществе. Если в веществе существует пространственная неоднородность плотности, температуры или скорости упорядоченного движения отдельных слоев вещества, то на беспорядочное тепловое движение молекул вещества накладывается упорядоченное движение, которое ведет к выравниванию этих неоднородностей. Эти явления называются явлениями переноса.

Таким образом, явления переноса – это группа явлений, обусловленных хаотическим тепловым движением молекул и приводящих к направленному переносу энергии (теплопроводность), количества движения (внутреннее трение) или массы (диффузия). Во всех трех явлениях имеется много общего, а именно в среде происходит направленный перенос какой-либо физической величины (энергии, количества движения, массы) из одной части вещества в другую до тех пор, пока данная величина не распределится равномерно по всему объему.

2)Диффузия (лат. diffusio — распространение, растекание, рассеивание, взаимодействие) — процесс взаимного проникновения молекул или атомов одного вещества между молекулами или атомами другого, приводящий к самопроизвольному выравниванию их концентраций по всему занимаемому объёму.

3)Коэффициентом диффузии называют физическую величину, которая численно равна количеству диффундирующего вещества, которое проникает за единицу времени через единицу поверхности, если разность плотностей на двух поверхностях, находящихся на расстоянии равном единице длины, равна единице.

В соответствии с кинетической теорией газов коэффициент диффузии можно вычислить как:

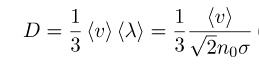
где U — средняя скорость теплового движения молекул; h— средняя длина свободного пробега; n — концентрация молекул, ᵟ— эффективное поперечное сечение соударения молекул.

Согласно кинетической теории газов коэффициент диффузии связан с другими коэффициентами переноса, например, с коэффициентом вязкости(ή)

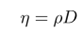
4)Закон Фика. Средняя скорость течения газа определяется формулой

Вопрос

Явления переноса. Теплопроводность. Коэффициент теплопроводности. Закон Фурье.

Явление переноса - В результате хаотического движения молекул и соударений между ними происходят непрерывные изменения их скоростей и энергий в веществе. Если в веществе существует пространственная неоднородность плотности, температуры или скорости упорядоченного движения отдельных слоев вещества, то на беспорядочное тепловое движение молекул вещества накладывается упорядоченное движение, которое ведет к выравниванию этих неоднородностей. Эти явления называются явлениями переноса.

Таким образом, явления переноса – это группа явлений, обусловленных хаотическим тепловым движением молекул и приводящих к направленному переносу энергии (теплопроводность), количества движения (внутреннее трение) или массы (диффузия). Во всех трех явлениях имеется много общего, а именно в среде происходит направленный перенос какой-либо физической величины (энергии, количества движения, массы) из одной части вещества в другую до тех пор, пока данная величина не распределится равномерно по всему объему.

Теплопроводность -способность материальных тел к переносу энергии (теплообмену) от более нагретых частей тела к менее нагретым частям тела, осуществляемому хаотически движущимися частицами тела (атомами, молекулами, электронами и т. п.). Такой теплообмен может происходить в любых телах с неоднородным распределением температур, но механизм переноса теплоты будет зависеть от агрегатного состояния вещества.

Коэффициент теплопроводности - в газах коэффициент теплопроводности может быть найден по приближённой формуле.

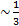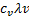X p = Dp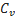

λ- средняя длина свободного пробега молекул газа

v- средняя тепловая скорость

p- плотность газа, а не давление

1. 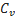- удельная теплоёмкость при постоянном объёме

Многие коэф. есть в таблице коэффициентов теплопроводности различных материалов.

Закон теплопроводности Фурье –

{\displaystyle {\vec {q}}}

Вязкость.

Вя́зкость (вну́треннее тре́ние) — одно из явлений переноса, свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. В результате работа, затрачиваемая на это перемещение, рассеивается в виде тепла.

Сила вязкого трения, действующая по площади 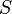на слой жидкости (газа), параллельный скорости течения 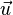, со стороны нижележащего слоя дается законом Ньютона:

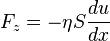
Велична 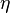называется коэффициентом вязкости.

Закон вязкости Ньютона.

Закон вязкости Ньютона-это выражающая пропорциональность напряжения трения междудвумя слоями прямолинейно движущейся вязкой жидкости относительной скоростискольжения этих слоев, т. е. отнесённому к единице длины изменению скоростипо нормали к направлению движения. В соответствиис этим законом напряжения трения т, действующее на поверхности элементарногообъёма жидкости или газа, пропорц. градиенту скорости du/dy, где и- составляющая скорости жидкости вдоль поверхности, а у - координата, <нормальная поверхности:

Коэф. пропорциональности 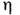наз. <коэф. внутр. трения жидкости или динамич. коэф. вязкости

Диффузия.

Закон Фика. Средняя скорость течения газа определяется формулой

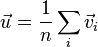
где суммирование выполняется по всем молекулам газа в единице объема. Плотность потока частиц равна

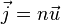
Помимо движения газа как целого существет процесс пространственного перераспределения компонент смеси относительно друг друга, обусловленный случайным движением молекул. Это неравновесный процесс, который называется диффузией.

Пусть имеется бинарная смесь с плотностью .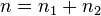

Пусть средняя скорость тесения газа 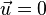, а диффузия осуществляется только вдоль оси 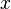. Тогда плотности потоков компонентов смеси даются законом Фика:

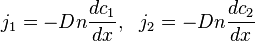
Следует, что 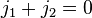. Это означает, что диффузия сама по себе не менят плотности среды.

Величина 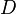называется коэффициентом диффузии.

Если 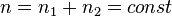, то формула закона Фика принимают более простой вид

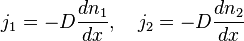
Теплопроводность.

Теплопроводность - это один из видов переноса тепла от более нагретых частей вещества к менее нагретым.

Плотность потока тепла 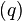- это кол-во тепловой энергии, пересекающей единичную площадь за единицу времени.

Для одномерного переноса тепла плотность потока тепла определяется законом Фурье:

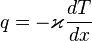
Величина 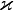называется коэффициентом теплопроводности.

В трехмерном случае плотность потока тепла - вектор

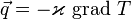
Вязкость.

Сила вязкого трения, действующая по площади 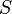на слой жидкости (газа), параллельный скорости течения 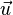, со стороны нижележащего слоя дается законом Ньютона:

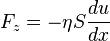
Велична 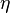называется коэффициентом вязкости.

Коэффициент пропорциональности, зависящий от природы жидкости или газа, называют коэффициентом динамической вязкости

Закон вязкости (внутреннего трения) Ньютона — математическое выражение, связывающее касательное напряжение внутреннего трения τ {\displaystyle \tau } (вязкость) и изменение скорости среды v {\displaystyle v} в пространстве ∂ v / ∂ n {\displaystyle \partial v/\partial n} (градиент скорости) для текучих тел (жидкостей и газов):

τ = η ∂ v ∂ n , {\displaystyle \tau =\eta {\frac {\partial v}{\partial n}},}

где величина η {\displaystyle \eta } называется коэффициентом внутреннего трения или коэффициентом динамической вязкости (единица СГС — пуаз); с физической точки зрения она представляет собой удельную силу трения при градиенте скорости, равном единице.

В технике, в частности, при расчёте гидроприводов и в триботехнике, часто приходится иметь дело с величиной:

ν = η ρ , {\displaystyle \nu ={\frac {\eta }{\rho }},}

эта величина получила название кинематической вязкости, единица СГС — Стокс. Здесь ρ {\displaystyle \rho } — плотность среды; η {\displaystyle \eta } — коэффициент динамической вязкости.

Закон Ньютона может быть получен аналитически и приёмами физической кинетики, где вязкость рассматривается обычно одновременно с теплопроводностью и соответствующим законом Фурье для теплопроводности. В кинетической теории газов коэффициент внутреннего трения вычисляется по формуле

η = 1 3 ⟨ u ⟩ ⟨ λ ⟩ ρ , {\displaystyle \eta ={\frac {1}{3}}\left\langle u\right\rangle \left\langle \lambda \right\rangle \rho ,}

где ⟨ u ⟩ {\displaystyle \left\langle u\right\rangle } — средняя скорость теплового движения молекул, ⟨ λ ⟩ {\displaystyle \left\langle \lambda \right\rangle } − средняя длина свободного пробега.

17. Процессы. Работа газа при различных процессах.

Применим первое начало термодинамики к некото-рым процессам в идеальном газе, при которых один из термодинамических параметров остаётся постоянным.

Такие процессы называются изопроцессы.

· Изохорический процесс (V=const)

В этом процессе газ не совершает работы: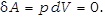

Поэтому всё тепло, сообщаемое газу, идёт на увеличе-ние его внутренней энергии: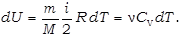

· Изобарический процесс (p=const)

При изобарическом процессе давление газа остаётся постоянным, поэтому работа газа будет равна: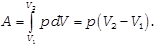

Если применить к полученному выражению уравнение состояния идеального газа, то выражение для работы газа в изобарическом процессе примет вид: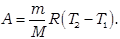

Первое начало термодинамики в этом процессе можно записать в виде: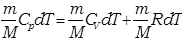

· Изотермический процесс (T=const)

·

Определим работу газа в изотермическом процессе.

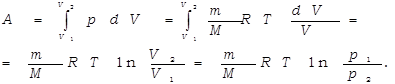
Так как в изотермическом процессе внутренняя энергия идеального газа не изменяется 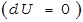, то всё количество теплоты, подводимое к газу, расходуется на совершение им работы против внешних сил.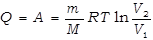

Теплоёмкость газа в изотермическом процессе бесконечно велика 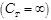, так как изменение температуры в изотермическом процессе равно нулю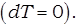

· Адиабатный процесс

Адиабатическим называется процесс, при котором отсутствует теплообмен между системой (газом) и окружающей средой.

Сосуды с теплонепроницаемыми стенками называются адиабатическими оболочками.

Для адиабатического процесса 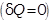первое начало термодинамики примет вид: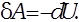

Для одного моля это выражение примет вид: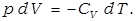

Используя уравнение состояния идеального газа, исключим давление из этого уравнения: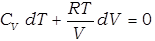

или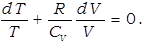

Произведя интегрирование, получим: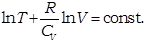

Потенцируя это выражение, имеем: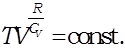

Учитывая, что 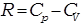,а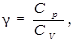

После несложных алгебраических преобразований получим:

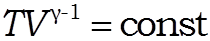или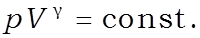

Уравнение адиабаты идеального газа в переменных и называется уравнением Пуассона.

Безразмерная величина 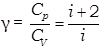называется показателем адиабаты или коэффициентом Пуассона.

Для одноатомных газов (i=3) y=1,67

для двухатомных –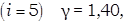

для многоатомных – .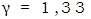

В координатах p и V процесс адиабатического расширения или сжатия газа изображается кривой, которая называется адиабатой.

При адиабатическом расширении газ совершает положительную работу, поэтому его внутренняя энергия уменьшается, а температура понижается.

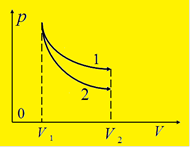
Вследствие этого давление газа при адиабатическом (2) расширении убывает быстрее, чем при изотермическом (1), а работа газа будет меньше.

Вычислим работу газа в адиабатическом процессе.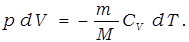

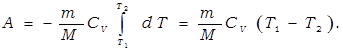
Этому выражению можно придать иной вид, если воспользоваться уравнением Майера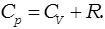

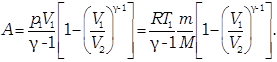
· Политропный процесс – такой процесс, при котором изменяются все основные параметры системы, кроме теплоемкости, т.е. С = const.

Уравнение политропы 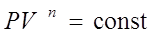или

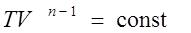
Здесь n– показатель политропы.

С помощью показателя n можно легко описать любой изопроцесс

1. Изобарный процесс Р = const, n = 0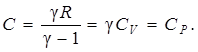

2. Изотермический процесс Т = const, n = 1,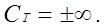

3. Изохорный процесс V = const, ,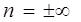

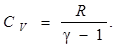
4. Адиабатический процесс DQ = 0, n = γ, С_ад = 0

Во всех этих процессах работу можно вычислить по одной формуле:

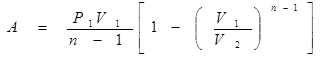
Распределение частиц по потенциальным энергиям. Барометрическая формула. Распределение Больцмана.

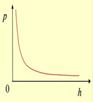Барометрическая формула .Барометрическая формула – зависимость давления газа от высоты (в поле тяготения Земли).

Два процесса:

1. тяготение,

2. тепловое хаотичное движение молекул приводят к некоторому стационарному состоянию.

Два процесса:

1. тяготение,

2. тепловое хаотичное движение молекул приводят к некоторому стационарному состоянию.

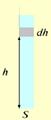Предположим:

1) идеальный газ, m = const,

2) поле тяготения однородно, g = const,

3) T = const. сила давления столба воздуха высотой dh сечением S.

m – масса молекулы.

n – концентрация молекул.

.

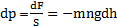Знак «–» отражает то, что с увеличением h давление p падает.

.

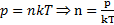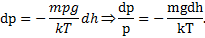
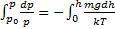
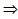
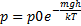
Применение: прибор для измерения высоты над поверхностью земли – высотомер (альтиметр). Для концентрации молекул.

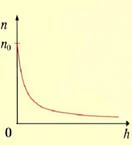
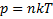
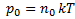
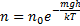
Распределение молекул по потенциальным энергиям

(Распределение Больцмана)

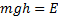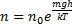, потенциальная энергия в поле тяготения

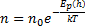- распределение Больцмана. Больцман показал, что распределение такого вида справедливо для любого внешнего поля.

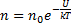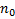- – концентрация молекул с нулевой потенциальной энергией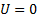

23. Энтропия. Второе начало термодинамики. Теорема Нернста.

Энтропи́я (поворот, превращение) — в естественных науках мера неупорядоченности системы, состоящей из многихэлементов. В частности, в статистической физике — мера вероятности осуществления какого-либо макроскопического состояния; Явление, обратное энтропии, именуется негэнтропией. Понятие энтропии впервые было введено Клаузиусом в термодинамике в 1865 году для определения меры необратимого рассеивания энергии, меры отклонения реального процесса от идеального. Определённая как сумма приведённых теплот, она является функцией состояния и остаётся постоянной при замкнутых обратимых процессах, тогда как в необратимых — её изменение всегда положительно.

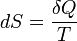
где 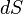— приращение энтропии; 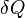— минимальная теплота, подведённая к системе; 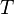— абсолютная температура процесса.

Второе начало термодинамики — физический принцип, накладывающий ограничение на направление процессов передачи тепла между телами. Второе начало термодинамики запрещает так называемые вечные двигатели второго рода, показывая, что коэффициент полезного действия не может равняться единице, поскольку для кругового процесса температура холодильника не может равняться абсолютному нулю (невозможно построить замкнутый цикл, проходящий через точку с нулевой температурой).

Второе начало термодинамики является постулатом, не доказываемым в рамках термодинамики. Оно было создано на основе обобщения опытных фактов и получило многочисленные экспериментальные подтверждения. Существуют несколько эквивалентных формулировок второго начала термодинамики:

Постулат Клаузиуса: «Невозможен процесс, единственным результатом которого являлась бы передача тепла от более холодного тела к более горячему» (такой процесс называется процессом Клаузиуса).

Постулат Томсона (Кельвина): «Невозможен круговой процесс, единственным результатом которого было бы производство работы за счет охлаждения теплового резервуара» (такой процесс называется процессом Томсона).

Эквивалентность этих формулировок легко показать. В самом деле, допустим, что постулат Клаузиуса неверен, то есть существует процесс, единственным результатом которого была бы передача тепла от более холодного тела к более горячему. Тогда возьмем два тела с различной температурой (нагреватель и холодильник) и проведем несколько циклов тепловой машины, забрав тепло 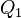у нагревателя, отдав 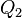холодильнику и совершив при этом работу 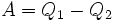. После этого воспользуемся процессом Клаузиуса и вернем тепло 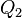от холодильника нагревателю. В результате получается, что мы совершили работу только за счет отъёма теплоты от нагревателя, то есть постулат Томсона тоже неверен. С другой стороны, предположим, что неверен постулат Томсона. Тогда можно отнять часть тепла у более холодного тела и превратить в механическую работу. Эту работу можно превратить в тепло, например, с помощью трения, нагрев более горячее тело. Значит, из неверности постулата Томсона следует неверность постулата Клаузиуса.

Таким образом, постулаты Клаузиуса и Томсона эквивалентны.

Другая формулировка второго начала термодинамики основывается на понятии энтропии:

«Энтропия изолированной системы не может уменьшаться» (закон неубывания энтропии).

Такая формулировка основывается на представлении об энтропии как о функции состояния системы, что также должно быть постулировано.

Второе начало термодинамики в аксиоматической формулировке Рудольфа Юлиуса Клаузиуса имеет следующий вид:

Для любой квазиравновесной термодинамической системы существует однозначная функция термодинамического состояния 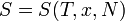, называемая энтропией, такая, что ее полный дифференциал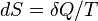

В состоянии с максимальной энтропией макроскопические необратимые процессы (а процесс передачи тепла всегда является необратимым из-за постулата Клаузиуса) невозможны.

Третье начало термодинамики (теорема Нернста) — физический принцип, определяющий поведение энтропии при приближении температуры к абсолютному нулю. Является одним из постулатов термодинамики, принимаемым на основе обобщения значительного количества экспериментальных данных.

Формулировка

Третье начало термодинамики может быть сформулировано так:

«Приращение энтропии при абсолютном нуле температуры стремится к конечному пределу, не зависящему от того, в каком равновесном состоянии находится система».

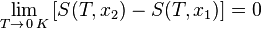
Или

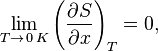
где 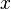— любой термодинамический параметр.

Третье начало термодинамики относится только к равновесным состояниям.

Поскольку на основе второго начала термодинамики энтропию можно определить только с точностью до произвольной аддитивной постоянной (то есть, определяется не сама энтропия, а только её изменение):

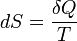
Третье начало термодинамики может быть использовано для точного определения энтропии. При этом энтропию равновесной системы при абсолютном нуле температуры считают равной нулю.

Третье начало термодинамики позволяет находить абсолютное значение энтропии, что нельзя сделать в рамках классической термодинамики (на основе первого и второго начал термодинамики). В классической термодинамике энтропия может быть определена лишь с точностью до роизвольной аддитивной постоянной 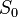, что не мешает термодинамическим исследованиям, так как реально измеряется разность энтропий 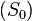в различных состояниях. Согласно третьему началу термодинамики, при 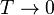значение .

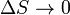В 1911 году Макс Планк сформулировал третье начало термодинамики как условие обращения в нуль энтропии всех тел при стремлении температуры к абсолютному нулю: 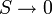. Отсюда 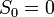, что даёт возможность определять абсолютное значения энтропии и других термодинамических потенциалов. Формулировка Планка соответствует определению энтропии в статистической физике через термодинамическую вероятность 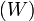состояния системы 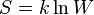. При абсолютном нуле температуры система находится в основном квантово-механическом состоянии. Если оно невырожденно, то 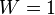(состояние реализуется единственным микрораспределением) и энтропия 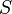при 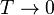равна нулю. В действительности при всех измерениях стремление энтропии к нулю начинает проявляться значительно раньше, чем могут стать существенными дискретность квантовых уровней макроскопической системы и влияние квантового вырождения.