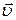Методические указания по курсу

ПСКОВСКИЙ ГОСУДАРСТВЕННЫЙ

ПОЛИТЕХНИЧЕСКИЙ ИНСТИТУТ

Кафедра физики

Вяткина Т.А., Лукин А.Е.

МОЛЕКУЛЯРНАЯ ФИЗИКА

ОПТИКА

ЯДЕРНАЯ ФИЗИКА

Методические указания по курсу

«Общефизический лабораторный практикум»

Псков

Издательство ППИ

СОДЕРЖАНИЕ

Работа 2.01 Измерение теплопроводности газа………………………… 4

Работа 2.02 Измерение температуры и теплоты плавления олова...…. 10

Работа 2.03 Изучение вращения плоскости поляризации…………….. 14

Работа 2.04 Измерение длины световой волны с помощью дифракцион-

ной решетки и проверка соотношения неопределенностей

для фотонов…………..…… ……………………………….. 21

Работа 2.05 Изучение законов внешнего фотоэффекта и определение

постоянной Планка…………………………………………. 26

Работа 2.06 Изучение излучения нити лампы накаливания и определение

постоянной Планка………………….……………………… 31

Работа 2.07 Спектроскопическое определение постоянной Планка….. 36

Работа 2.08 Определение состава латуни и бронзы спектральным

методом при помощи стилоскопа………………………….. 42

Работа 2.09 Изучение треков заряженных частиц……………………… 46

Приложение I. Правила оформления отчета……………………………

Приложение II.Таблицы

Лабораторная работа 2.01

Измерение теплопроводности газа

Цель работы: исследовать температурную зависимость коэффициента теплопроводности воздуха.

Принадлежности: цифровой вольтметр В7-27, стрелочный вольтметр, источник питания ВС-24М, «стенд» с исследуемым образцом.

ТЕОРИЯ

Явление теплопроводности представляет собой процесс переноса тепла, обусловленный беспорядочным движением молекул. Если размеры тел, в которых рассматривается перенос тепла, значительно превосходят длины свободного пробега молекул, можно рассматривать вещество как сплошную среду. Тогда основным понятием теории теплопроводности становится температурное поле – совокупность мгновенных значений температур во всех точках среды

.

Если температурное поле зависит и от координат и от времени , то оно называется нестационарным. Температурное поле, не изменяющееся во времени и зависящее, следовательно, только от координат, называется стационарным:

.

В простейшем случае, когда температурное поле зависит только от одной координаты, оно называется одномерным:

.

Точки тела, имеющие одинаковые температуры, образуют изотермические поверхности. Так как одна и та же точка тела не может одновременно иметь различные температуры, изотермические поверхности не могут пересекаться. Они либо оканчиваются на поверхности теплопроводящего тела, либо замыкаются внутри него. В простейших одномерных полях изотермические поверхности представляют собой параллельные плоскости, коаксиальные цилиндрические поверхности с общим центром.

Важной характеристикой поля является градиент. Градиент температуры определяется как вектор, направленный по нормали (перпендикулярно) к изотермической поверхности в сторону возрастания температуры и численно равный изменению температуры на единице расстояния между изотермическими поверхностями. Для поля, изотермическими поверхностями которого являются цилиндры:

. (1)

Градиент температуры измеряется в .

Для переноса тепла в любом веществе необходимо и достаточно существования в нем отличного от нуля градиента температур. При этом между изотермическими поверхностями возникает тепловой поток. Для его характеристики вводится понятие плотности теплового потока q, которая представляет собой количество тепла, протекающего через единицу площади изотермической поверхности в единицу времени:

. (2)

Так как тепло передается от более горячих частей тела к холодным, плотность теплового потока есть величина векторная, направленная противоположно вектору градиента температуры.

Опытный закон Фурье утверждает, что плотность теплового потока пропорциональна градиенту температуры:

. (3)

Коэффициент 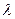называется коэффициентом теплопроводности. В системе СИ он измеряется в . Если процесс переноса тепла стационарен, а между изотермическими поверхностями нет источников или стоков тепла, полный тепловой поток через такие поверхности должен быть одинаков.

Одним из таких методов измерения коэффициента теплопроводности газов является метод нагретой нити. В этом методе исследуемый газ находится в цилиндрической трубке, по оси которой натянута проволока из платины, никеля или другого металла, служащая одновременно источником тепла. Наружная поверхность трубки поддерживается при постоянной температуре, а через проволоку пропускается электрический ток, в результате чего проволока нагревается. Разность температур проволоки и стенок трубки и приводит к возникновению теплового потока. Динамическое равновесное состояние установится, когда выделяемое при прохождении электрического тока тепло будет равно количеству тепла, уносимого за счет теплопроводности. Если принять, что тепло идет от проволоки через газ только по радиусу, то изотермическими поверхностями в газе будут цилиндрические поверхности с общей осью – осью проволоки. Равновесие установится, когда величина мощности будет равна потоку тепла, уходящего за счет теплопроводности и условие равновесия будет соответствовать равенству:

, (4)

где q – плотность теплового потока, соответствующего уравнению (3). Подставляя (3) в (4), получаем

, (5)

Выражение (5) представляет собой дифференциальное уравнение с разделяемыми переменными:

. (6)

Интегрируя (6), получаем:

. (7)

В уравнении (7) содержатся две неизвестные: постоянная интегрирования С и коэффициент теплопроводности 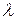. Для их вычисления используем следующие граничные условия:

при , при . (8)

Здесь и - температуры слоев газа, непосредственно прилегающих к поверхностям проволоки и трубки с соответствующими радиусами и . После простых выкладок получим формулу для расчета коэффициента теплопроводности:

. (9)

Для определения необходимо измерить температуры и , которые отождествляются с температурами поверхностей нити и трубки, а также мощность нагревателя и геометрические размеры , , L, которые в нашей лаборатории задаются студенту.

При реализации такого метода возникает ряд источников систематических погрешностей, с которыми необходимо считаться при постановке измерений и обработке их результатов. Рассмотрим важнейшие из них.

Конвективный перенос тепла

Теплопроводность определяется тепловым движением молекул газа. При конвективном механизме тепло переносится движение макроскопических объемов газа. Оно может быть обусловлено разностью плотностей нагретого и холодного газа (естественная конвекция). Конвекция может сильно исказить результаты измерения коэффициента теплопроводности. Роль конвекции в переносе тепла тем существеннее, чем больше разность температур . Для уменьшения искажающего влияния конвекции на результаты измерений можно воспользоваться тем, что, начиная с некоторой разности температур, это влияние резко возрастает. В нашем приборе температура внешней стенки практически одинакова в разных режимах. Поэтому можно построить зависимость измеренного значения 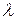от температуры нити или средней температуры газа. До температур, где это значение резко растет с Т, можно считать, что изучалась зависимость коэффициента теплопроводности от температуры. При более высоких температурах влияние конвекции становится подавляющим, а измерение коэффициента теплопроводности в данном приборе – практически невозможным.

Перенос тепла излучением

Тепловое излучение поверхности нагретой нити является также дополнительным механизмом переноса тепла, который может быть учтен введением соответствующей поправки. Плотность теплового потока, возникающего вследствие излучения, определяется формулой Стефана-Больцмана:

, (11)

в которой - степень черноты поверхности никелевой проволоки, равная 0,44; - постоянная Стефана-Больцмана; и - абсолютные температуры поверхностей нити и трубки соответственно, S – площадь поверхности рабочего участка нити, определяемая по формуле:

.

С учетом поправки (11) формула (10) преобразуется к виду:

. (12)

Как следует из формулы (11), величина поправки на излучение быстро растет с увеличением температуры нити. Относительный вклад поправки на излучение можно определить, сравнивая мощность излучения с полной электрической мощностью, выделяемой на рабочем участке нити:

. (13)

Описание установки

Рабочий участок установки показан на рис. 2.

Никелевая проволока диаметром расположена по оси вертикальной стеклянной трубки внутренним диаметром , заполненной воздухом. Внешняя стеклянная трубка диаметром D образует кожух для воды. Тепловой поток, идущий через воздух от нагретой проволоки, нагревает прилегающие к внутренней трубке слои воды. Вследствие теплового расширения плотность этих слоев воды уменьшается. Разность плотностей вызывает движение – циркуляцию жидкости и непрерывное обновление слоев, прилегающих к трубке. Из-за большой теплоемкости и значительного объема воды изменение ее температуры в течение опыта незначительно, поэтому можно считать, что температура внутренней стеклянной трубки ( ) равна температуре воды, т.е. комнатной температуре, которая определяется по термометру в лаборатории. Проволока ориентирована по оси трубки с помощью втулок. Рабочий участок схемы имеет два токоподвода и три потенциальных вывода, которые позволяют произвести измерение падений напряжения и на двух участках проволоки.

Подключение вольтметра осуществляется с помощью тумблера Тум. Ток в цепи проволоки рассчитывается по закону Ома:

, (14)

где измеряется вольтметром , указано на плате установки.

Сопротивление R служит для ограничения тока в цепи питания проволоки. Сопротивления участков проволоки и также рассчитываются по закону Ома для участка цепи:

; , (15)

где и измеряются вольтметром , I – ток в цепи проволоки, рассчитанный по формуле (14).

Температура проволоки определяется по ее сопротивлению. При этом рассматривается центральный участок проволоки с сопротивлением:

, (16)

которое зависит от температуры, по формуле:

и, следовательно,

. (17)

Здесь - температурный коэффициент сопротивления никеля, - сопротивление исследуемого участка нити при комнатной температуре определяется экстраполяцией, т.е. продолжением графика в точку .

Значения , , указаны на плате установки.

Порядок выполнения работы

1. Собрать электрическую схему установки.

2. Включите в сеть и подготовить к работе вольтметры и .

3. Включить в сеть выпрямитель ВС-24М, предварительно установив ручку регулировки напряжения в положение, соответствующее, минимальному напряжению.

4. Измерить и записать температуру воздуха в лаборатории .

5. Переводя регулятор напряжения на лицевой панели выпрямителя вправо, записать показание вольтметра и, переключая тумблер, с помощью вольтметра , определять напряжения и . При этом вследствие тепловой инерции измерительной ячейки переход от одного установившегося теплового состояния к другому происходит через определенный интервал времени, увеличивающийся с ростом тока в цепи. О достижении стационарности процесса можно судить по показаниям вольтметров: записывать их показания следует только после того, как они перестают изменяться. В процессе эксперимента заполняйте таблицу 1.

Таблица 1

	Положение тумблера	Примечание: Цена деления ( )
деления	В	, В	, В

Обработка результатов

1. В процессе обработки результатов заполняется таблица 2.

2. Для каждого измерения вычислить силу тока по формуле (13), сопротивление участка нити по формуле (15). Построить график зависимости и экстраполяцией в область определить .

3. По формуле (16) вычислить перепад температур — и коэффициент теплопроводности 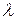для каждого измерения по формуле (11).

4. Вычислить величины поправок на излучении для трех значений в начале, середине и конце диапазона. Сделать выводы о роли и величине поправок.

5. Построить зависимость , принимая за температуру газа, к которой относится экспериментальный результат, среднюю температуру .

Таблица 2

I, А	, В	, Ом	, Ом	, К	, К	, К	,

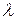Контрольные вопросы

1. Перечислите способы теплообмена.

2. Сформулируйте закон Фурье.

3. В чем физический смысл знака «минус» в законе Фурье?

4. Определение плотности теплового потока и градиента температуры (направление, модуль, наименование).

5. Определение изотермической поверхности (вид изотермической поверхности в нашей работе).

6. В чем измеряется коэффициент теплопроводности ?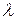

7. Вывод расчетной формулы для .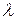

8. Каким образом в работе находится ?

9. Физический смысл формулы (4).

10. Как измеряется температура нити?

Литература

1. А.А.Детлаф, Б.М.Яворский, Л.Б.Милковская. Курс физики, М., «Высшая школа», 1973, т.1.

2. Г.А.Зисман, О.М.Тодес. Курс общей физики, М., «Наука», 1972, т.1.

3. И.В.Савельев Курс общей физики, т. 1, М., «Астрель», 2005.

Лабораторная работа 2.02

ТЕОРИЯ

Переход твердого вещества в жидкое (плавление) и обратный переход (кристаллизация) относятся к фазовым превращениям первого рода, при которых скачком изменяется плотность, внутренняя энергия, энтропия тела. При этом поглощается (при плавлении) или выделяется (при кристаллизации) энергия, называемая теплотой плавления (кристаллизации).

При заданном давлении прямое и обратное фазовые превращения происходят при строго определенной температуре, поэтому изобарный фазовый переход одновременно является изотермическим. Одним из возможных способов измерения температуры и теплоты плавления является получение диаграммы плавления (или отвердевания), т.е. кривой зависимости температуры расплавляемого (или отвердевающего) вещества от времени при неизменных внешних условиях. Для получения диаграмм сосуд (тигель) с исследуемым веществом помещают в печь и, нагревая его измеряют через определенные промежутки времени (или непрерывно с помощью самописца) температуру вещества в тигле.

В качестве термометра, находящегося в непосредственном контакте с исследуемым веществом используют термопару. Действие термопары основано на том, что в спае двух разнородных проводников возникает контактная термоэлектродвижущая сила (ТЭДС), примерно пропорциональная температуре спая. Чаще всего приходится использовать не менее трех материалов: два – для электродов термопары и один – для обмотки измерительного прибора, что дает несколько спаев. Обычно используют схему, показанную на рис. 1. Так называемый «горячий» спай Т приводят в контакт с испытуемым телом. Оба «холодных спая 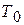должны находиться при одинаковой и известной температуре. ТЭДС для схемы рис.1 приблизительно пропорциональна разности температур Т и :

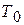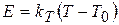. (1)

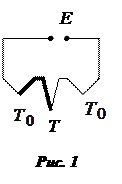Если холодные спаи держать при температуре льда 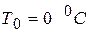, то ТЭДС пропорциональна температуре горячего спая Т по шкале Цельсия. Обычно для этого случая и приводят коэффициент 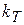или градуировку термопары в форме графика (таблицы). Если же холодные спаи имеют температуру 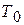, отличную от 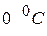, измеренному значению ТЭДС соответствует разность температур .

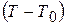В данной работе роль холодных спаев выполняют контакты проводов термопары с клеммами измерительного прибора (потенциометра), которые имеют комнатную температуру. Поэтому определение температуры сводится к следующему. Измерить комнатную температуру 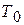, Измерить ТЭДС Е. По измеренному значению ТЭДС и градуировочной таблице 1 определить 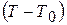и, прибавив 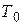, найти искомую температуру Т.

На рис. 2 качественно изображен процесс медленного остывания и кристаллизации металлической пробы, помещенной в тигель. При достаточно медленном остывании можно считать, что температуры Т пробы и тигля одинаковы во всех точках. Эти температуры отложены на рис. 2 по вертикальной оси. Если тепловая мощность, подводимая к образцу, может считаться постоянной, ось времени (горизонтальная на рис.2) является одновременно и осью «теплоты, отдаваемой образцом и тиглем».

Тепловая мощность N конечно не равна мощности нагревателя, т.к. часть теплоты отводится в окружающую среду. Левая и правая убывающие части кривой на рис. 2 изображают остывание расплава и тигля (слева) и остывание твердого образца и тигля (справа). Тепловая мощность на одном из этих участков равна изменению внутренней энергии системы в единичное время:

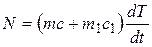. (2)

Массы пробы металла т и тигля 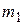, а также их удельные теплоемкости с и 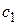, вблизи температуры плавления известны. Горизонтальный участок на рис.2 изображает процесс плавления металла. Ордината его – температура плавления, а приращение абсциссы – время фазового перехода 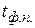. Здесь выполняется равенство

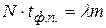, (3)

где 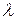- удельная теплота плавления. Исключив N из формул (2) и (3), найдем

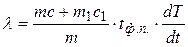. (4)

Экспериментальная установка

Схема лабораторной установки приведена на рис.3. Установка состоит из электрического нагревателя (печи) 2, регулятора напряжения и кварцевого тигля 3, заполненного испытуемым металлом (здесь оловом). В металл погружены две термопары: 4 – с записью ее ТЭДС на ленточной диаграмме электронного потенциометра ЭП и 5 – с измерением ТЭДС вручную, с помощью потенциометра типа ПП-63. Градуировочная таблица термопар при температуре холодного спая 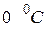дана в таблице 2.

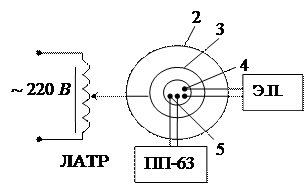
Рис. 3

Порядок выполнения работы

Диаграмма плавления (или отвердевания) металла может быть получена путем измерения ТЭДС вручную или с помощью электронного потенциометра. Второй прибор можно использовать для дополнительного контроля.

1. Измерить температуру холодного спая (комнатную температуру) с помощью лабораторного термометра.

2. Подготовить к работе потенциометр ПП-63 (см. инструкции на рабочем столе). Установить рабочий ток, измерить ТЭДС при начальных условиях. С помощью таблицы 2 найти начальную температуру металла.

3. Подготовить к работе электронный потенциометр, протяжку ленты включить на несколько секунд для проверки.

4. Установить регулятор напряжения печи в положение 100. Включить печь.

5. Измерение ТЭДС проводить вручную через равные промежутки времени. Результаты записать в таблицу 1. Можно автоматизировать эксперимент, регистрируя ТЭДС на ленте ЭП.

6. По достижении ТЭДС примерно 18 тВ выключить печь и записать диаграмму отвердевания (или измерить вручную). Поскольку при кристаллизации площадка постоянной температуры получается обычно более четкой, для определения теплоты плавления рекомендуется использовать диаграмму отвердевания пробы. В период собственной кристаллизации постоянную температуру фазового перехода 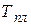измерить несколько раз с помощью потенциометра ПП-63.

Таблица 1

t, мин	Е, тВ	Т,	=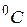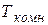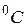
1. …

Обработка результатов

1. Пользуясь таблицей 2 и результатами измерения ТЭДС на участке 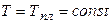, найти температуру плавления олова. Оценить погрешность измерения с учетом приборной погрешности потенциометра.

2. Используя диаграмму затвердевания олова, записанную на ленте потенциометра ЭП, определить удельную теплоту 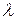плавления олова. Для этого:

a) 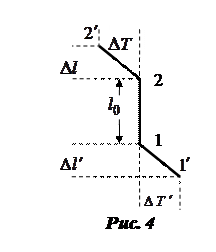отметить на диаграмме точки, соответствующие началу и концу процесса затвердевания (точки 1 и 2 на рис.4); измерить длину вертикального отрезка 1-2, соответствующего двухфазному состоянию; вычислить время затвердевания 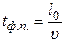, где 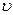- скорость протяжки ленты потенциометра.

b) выделить прямолинейные участки диаграммы вблизи области фазового перехода (участк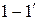и и 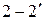на рис.4); определить по диаграмме соответствующие этим участкам приращения температуры 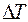и длины 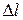. По формуле 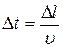вычислить приращение времени 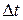; вычислить скорость охлаждения образца .

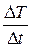с) с помощью формулы (4) вычислить удельную теплоту плавления металла.

3. Сравнить полученные результаты с табличными (приложение 3).

Примечание: поскольку в окрестности точек 2 и 1 кривая остывания не имеет четкого излома, для определения положения точек 2 и 1 необходимо экстраполировать участки 2- 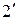, 2-1 и 1- 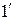прямыми линиями и определить положение точек 2 и 1 по пересечению этих линий.

Контрольные вопросы

1. Что называется температурой?

2. Какое превращение называется фазовым переходом первого рода?

3. Почему процесс плавления происходит при постоянной температуре?

4. Что называется удельной теплотой плавления?

5. Опишите метод измерения температуры с помощью термопары.

Литература

1. А.А.Детлаф, Б.М.Яворский, Л.Б.Милковская. Курс физики, М., «Высшая школа», 1973, т.1.

2. Г.А.Зисман, О.М.Тодес. Курс общей физики, М., «Наука», 1972, т.1.

3. И.В.Савельев Курс общей физики, т. 1, М., «Астрель», 2005.

Таблица 2. Градуировка термопары

	0,00	0,07	0,13	0,20	0,26	0,33	0,39	0,46	0,52	0,59
	0,65	0,72	0,78	0,85	0,91	0,98	1,05	1,11	1,18	1,24
	1,31	1,38	1,44	1,51	1,57	1,64	1,70	1,77	1,84	1,91
	1,98	2,06	2,14	2,22	2,30	2,38	2,46	2,54	2,62	2,70
…	…	…	…	…	…	…	…	…	…	…
	9,00	9,08	9,16	9,24	9,32	9,40	9,48	9,56	9,64	9,76
	9,84	9,92	10,0	10,08	10,16	10,24	10,32	10,40	10,48	10,56
	10,64	10,72	11,00	11,08	11,16	11,24	11,32	11,40	11,48	11,56
	11,62	11,67	11,72	11,77	11,82	11,87	11,92	11,97	12,02	12,15
	12,24	12,32	12,40	12,48	12,55	12,63	12,71	12,79	12,87	12,95
	13,03	13,11	13,19	13,27	13,36	13,44	13,52	13,60	13,68	13,76
	13,84	13,92	14,00	14,08	14,16	14,25	14,34	14,42	14,50	14,58
	14,66	14,74	14,82	14,90	14,98	15,06	15,14	15,22	15,30	15,38
	15,48	15,56	15,64	15,72	15,80	15,89	15,97	16,05	16,13	16,21
	16,30	16,38	16,46	16,54	16,62	16,71	16,79	16,86	16,95	17,03
	17,12	17,20	17,28	17,37	17,45	17,53	17,62	17,70	17,78	17,87
	17,95	18,03	18,11	18,19	18,28	18,36	18,44	18,52	18,61	18,70
	18,77	18,85	18,93	19,02	19,10	19,18	19,27	19,35	19,43	19,52
	19,60	19,68	19,76	19,85	19,93	20,01	20,10	20,18	20,26	20,65

Лабораторная работа 2.03

ТЕОРИЯ

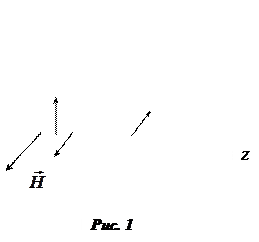
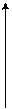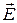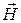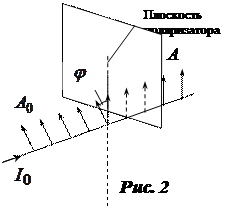
Согласно электромагнитной теории свет представляет собой поперечные электромагнитные волны с длиной волны, находящейся в диапазоне от 400 нм до 760 нм (рис. 1). Векторы напряженности электрического поля и магнитного поля световой волны взаимно перпендикулярны и перпендикулярны направлению распространения света (ось z). Плоскость, проходящая через 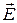и z называется плоскостью колебаний. Если плоскость колебаний сохраняет неизменное положение в пространстве, то свет называется плоско-поляризованным. В световых волнах, испускаемых обычными источниками света, плоскость колебаний быстро и беспорядочно меняет свою ориентацию. Такой свет называется естественным. Естественный свет можно преобразовать в поляризованный при помощи устройств, называемых поляризаторами (призма Николя, поляроиды). Эти приборы свободно пропускают колебания, параллельные плоскости, называемой плоскостью поляризатора, и полностью или частично задерживают колебания, перпендикулярные его плоскости. Пусть на поляризатор падает плоскополяризованный свет амплитуды 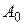и интенсивности 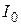(рис. 2). Сквозь прибор пройдет составляющая колебания с амплитудой

,

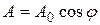где 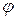- угол между плоскостью колебаний падающего света и плоскостью поляризатора. Следовательно, интенсивность прошедшего света I определяется выражением

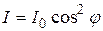. (1)

Соотношение (1) носит название закона Малюса.

В 1670 г. Иразм Бартолин обнаружил, что в прозрачных для видимой области кристаллах исландского шпата 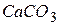происходит так называемое двойное лучепреломление. Это явление заключается в том, что упавший на кристалл луч разделяется внутри него на два луча, распространяющихся с разными скоростями и в различных направлениях. При этом один из преломленных лучей подчиняется обычному закону прел