Применимость метода симметричных составляющих к исследованию переходных процессов
Из курса теоретических основ электротехники известно, что в электрических устройствах, выполненных симметрично, применение метода симметричных составляющих в значительной мере упрощает анализ несимметричных процессов, так как при этом симметричные составляющие токов связаны законом Ома с симметричными составляющими напряжений только одноименной последовательности. Иными словами, если какой-либо элемент цепи симметричен и обладает по отношению к симметричным составляющим токов прямой 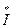 1, обратной
1, обратной 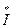 2 и нулевой
2 и нулевой 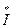 о последовательностей соответственно сопротивлениями Z1, Z2, Zo, то симметричные составляющие падения напряжения в этом элементе будут:
о последовательностей соответственно сопротивлениями Z1, Z2, Zo, то симметричные составляющие падения напряжения в этом элементе будут:
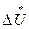 1 = Z1
1 = Z1 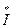 1 (11-1)
1 (11-1)
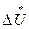 2 = Z2
2 = Z2 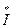 2 (11-2)
2 (11-2)
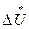 0 = Z0
0 = Z0 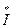 0 (11-3)
0 (11-3)
Сопротивления Z1, Z2 и Zo для сокращения обычно называют сопротивлениями соответственно прямой, обратной и нулевой последовательностей. Их величины для одного и того же элемента в общем случае различны (см. гл. 12).
Комплексная форма записи уравнений справедлива не только для стационарного режима, но также для переходного процесса [Л. 6], поскольку токи и напряжения при переходном процессе можно представить проекциями на .соответствующую ось вращающихся, а также неподвижных векторов. При этом дифференциальным уравнениям, связывающим комплексные значения токов и напряжений, соответствуют операторные уравнения, которые при нулевых начальных условиях 1 посвоей структуре аналогичны уравнениям стационарного режима, записанным в комплексной форме.
 1 К ним всегда можно свести любую задачу, используя принцип наложения.
1 К ним всегда можно свести любую задачу, используя принцип наложения.
Из изложенного, казалось бы, уже можно сделать вывод, что если временные величины в рассматриваемом процессе могут быть представлены комплексами или соответственно векторами, то последние в свою очередь могут быть разложены на системы симметричных составляющих и тогда известный метод симметричных составляющих в своей обычной форме может быть применен к исследованию несимметричных переходных процессов. Однако такой вывод был бы еще преждевременным.
Дело в том, что, как показано в предыдущем параграфе, у синхронной машины с несимметричным ротором возникающее при несимметричном режиме инверсное магнитное поле статора порождает прямое магнитное поле статора, вращающееся с соответственно большей скоростью. Обращаясь к терминологии метода симметричных составляющих, можно сказать, что это равносильно тому, что магнитное поле обратной последовательности, созданное системой токов обратной последовательности какой-либо частоты, вызывает магнитное поле прямой последовательности и связанную с ними систему токов прямой последовательности, порядковые номера частот которых на два больше соответствующего номера частоты токов обратной последовательности. Другими словами, при этом оказываются взаимно связанными системы токов прямой и обратной последовательностей разных частот, что налагает дополнительные условия и требования на метод симметричных составляющих. Что касается системы токов нулевой последовательности, то создаваемое ими результирующее магнитное поле в расточке статора при любой частоте практически близко к нулю и никакой магнитной связи с ротором не создает.
Дальнейшее развитие представлений метода симметричных составляющих применительно к синхронным машинам с несимметричным ротором в условиях установившихся режимов и переходных процессов при нарушении симметрии впервые дано Н. Н. Щедриным. Помимо математического обоснования такого развития,импредложены для учета высших гармоник специальные цепные схемы, применение которых особенно эффективно при выполнении расчетов с помощью моделей или иных расчетных установок.
Аналогичное предложение также сделано П. С. Ждановым.
В подавляющем числе практических расчетов несимметричных переходных процессов обычно довольствуются учетом лишь основной гармоники токов и напряжений. Именно только при таком ограничении представляется возможным применять метод симметричных составляющих в его обычной форме, характеризуя для этого синхронную машину в схеме обратной последовательности соответствующей реактивностью х2(см. §12-2).
Остановимся еще на одном вопросе, в понимании которого часто встречаются трудности.
Протекающие по обмоткам статора токи прямой, обратной и нулевой последовательностей создают магнитные потоки тех же последовательностей, а последние наводят в статоре соответствующие э. д. с. Вводить эти э. д. с. в расчет нецелесообразно, так как они пропорциональны (при пренебрежении насыщением магнитной системы машины) токам отдельных последовательностей, значения которых еще подлежат определению. Поэтому в дальнейшем вводим в расчет только те э. д. с., которые или известны, или не зависят от внешних условий цепи статора1, причем в силу симметричного выполнения статорной обмотки эти э. д. с. являются э. д. с. только прямой последовательности. Что касается э. д. с., обусловленных реакцией токов отдельных последовательностей, то их учитываем в виде падений напряжений с обратным знаком в соответствующих реактивностях машины.
Дополнительно примем, что установленные у синхронных машин устройства автоматического регулирования возбуждения независимо от их конструкции реагируют только на отклонения напряжения прямой последовательности (т. е. они включены через фильтры напряжения прямой последовательности) и стремятся поддержать это напряжение на постоянном уровне, которое принимается равным номинальному для каждой машины.
 1. Как-то: начальные значения переходной и сверхпереходной э. д. с., синхронная э. д. с. E q, при известном токе возбужденияIf, расчетная э. д. с. Et для произвольного момента времени согласно методу спрямленных характеристик и др.
1. Как-то: начальные значения переходной и сверхпереходной э. д. с., синхронная э. д. с. E q, при известном токе возбужденияIf, расчетная э. д. с. Et для произвольного момента времени согласно методу спрямленных характеристик и др.
В соответствии с изложенным для произвольного несимметричного короткого замыкания основные уравнения второго закона Кирхгофа отдельно для каждой последовательности будут иметь вид:
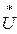 к1 =
к1 = 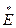 S - Z1S
S - Z1S 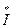 к1 (11-4)
к1 (11-4)
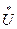 к2 = 0 – Z2S
к2 = 0 – Z2S 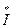 к2 (11-5)
к2 (11-5)
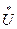 к0 = 0 – Z0S
к0 = 0 – Z0S 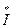 к0 (11-6)
к0 (11-6)
где 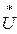 к1,
к1, 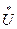 к2,
к2, 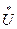 к0,
к0, 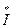 к1,,
к1,, 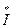 к2,
к2, 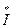 к0 —симметричные составляющие напряжения и тока в месте короткого замыкания;
к0 —симметричные составляющие напряжения и тока в месте короткого замыкания;
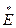 S - результирующая э. д. с. относительно точки короткого замыкания;
S - результирующая э. д. с. относительно точки короткого замыкания;
Z1S, Z2S, Z0S — результирующие сопротивления схем соответствующих последовательностей относительно точки короткого замыкания.
Из (11-5) и (11-6) непосредственно следует, что при принятом способе учета э. д. с., обусловленных реакцией токов отдельных последовательностей, образование токов обратной и нулевой последовательностей можно представить как следствие возникающих в месте короткого замыкания напряжений обратной и нулевой последовательностей.
При однократной продольной несимметрии (см. § 15-1) основные уравнения для каждой последовательности имеют тот же вид, что и (11-4)—(11-6), только вместо 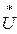 к1,
к1, 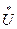 к2,
к2, 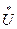 к0 в них следует ввести разности фазных напряжений соответствующих последовательностей по концам местной несимметрии, а сопротивления Z1S, Z2S, Z0S должны представлять собой результирующие сопротивления схем соответствующих последовательностей относительно места рассматриваемой продольной несимметрии.
к0 в них следует ввести разности фазных напряжений соответствующих последовательностей по концам местной несимметрии, а сопротивления Z1S, Z2S, Z0S должны представлять собой результирующие сопротивления схем соответствующих последовательностей относительно места рассматриваемой продольной несимметрии.
Уравнения (11-1) — (11-3) или (11-4) — (11-6) содержат шесть неизвестных величин: три составляющие напряжения и три составляющие тока.
Недостающие для определения этих величин три уравнения легко получить из граничных условий, которыми характеризуется тот или иной вид несимметричного повреждения.
Задача нахождения токов и напряжений при рассматриваемом несимметричном переходном процессе по существу сводится к вычислению симметричных составляющих этих величин. Как только последние найдены, дальнейшее определение фазных величин токов и напряжений производится по соотношениям1, известным из теории симметричных составляющих.
Глава двенадцатая
