Удельная теплоемкость. Виды теплоемкости. Уравнение Майера

Удельная теплоёмкость (С_уд) есть количество теплоты, необходимое для нагревания единицы массы вещества на 1 градус [C_уд] = Дж/К.

Для газов удобно пользоваться молярной теплоемкостью Cμ- количество теплоты, необходимое для нагревания 1 моля газа на 1 градус:

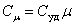(4.2.2)

[Cμ] = Дж/(моль×К).

Из п. 1.2 известно, что молярная масса – масса одного моля:

n/tr>

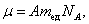где А – атомная масса; m_ед - атомная единица массы; N_А - число Авогадро; моль μ – количество вещества, в котором содержится число молекул, равное числу атомов в 12 г изотопа углерода ¹²С.

Теплоёмкость термодинамической системы зависит от того, как изменяется состояние системы при нагревании.

Если газ нагревать при постоянном объёме, то всё подводимое тепло идёт на нагревание газа, то есть изменение его внутренней энергии. Теплоёмкость при этом обозначается С_V.

С_Р – теплоемкость при постоянном давлении. Если нагревать газ при постоянном давлении Р в сосуде с поршнем, то поршень поднимется на некоторую высоту h, то есть газ совершит работу (рис. 4.2).

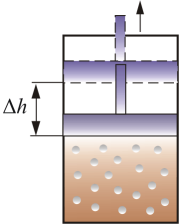
Рис. 4.2

Следовательно, проводимое тепло затрачивается и на нагревание и на совершение работы. Отсюда ясно, что .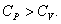

Итак, проводимое тепло и теплоёмкость зависят от того, каким путём осуществляется передача тепла. Значит, Q и С не являются функциями состояния.

Величины С_Р и С_V оказываются связанными простыми соотношениями. Найдём их.

Пусть мы нагреваем один моль идеального газа при постоянном объёме(dA = 0). Тогда первое начало термодинамики запишем в виде:

,

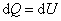(4.2.3)

т.е. бесконечно малое приращение количества теплоты 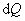равно приращению внутренней энергии dU.

Теплоемкость при постоянном объёме будет равна:

,

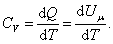(4.2.4)

В общем случае

,

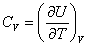так как U может зависеть не только от температуры. Но в случае идеального газа справедлива формула (4.2.4).

Из (4.2.4) следует, что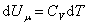

,

,

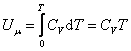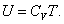(4.2.5)

Внутренняя энергия идеального газа является только функцией температуры (и не зависит от V, Р и тому подобных), поэтому формула (4.2.5) справедлива для любого процесса.

Для произвольной идеальной массы газа:

,

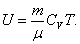(4.2.6)

При изобарическом процессе, кроме увеличения внутренней энергии, происходит совершение работы газом:

.

.

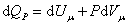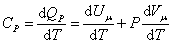(4.2.7)

Из основного уравнения молекулярно-кинетической теории 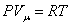. При изобарическом процессе Р = const. Следовательно, из (4.2.7) получим:

.

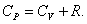(4.2.8)

Это уравнение Майера для одного моля газа.

Из этого следует, что физический смысл универсальной газовой постоянной в том, что R – численно равна работе, совершаемой одним молем газа при нагревании на один градус в изобарическом процессе.

Используя это соотношение, Роберт Майер в 1842 г. вычислил механический эквивалент теплоты: 1 кал = 4,19 Дж.

Полезно знать формулу Майера для удельных теплоёмкостей:

.

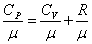или

.

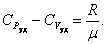Второй закон термодинамики

Согласно второму закону термодинамики теплота самопроиз­вольно может переходить только от более нагретого тела к менее нагретому. Установлено, что в работу может превращаться только часть той теплоты, которая переходит от нагревателя к холодиль­нику, и тем большая, чем больше разность температур:

A = q 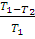(2. 24)

где q - теплота, отдаваемая нагревателем; T₁—температура на­гревателя; Т₂ — температура холодильника.

Отношение называется коэффициентом полезного действия (КПД) - η. Отсюда

η = 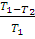(2.25)

На основе второго закона термодинамики Клаузиус ввел поня­тие энтропии S — термодинамической функции системы. Измене­ние энтропии ∆S в каком-либо процессе зависит только от начального и конечного состояний системы и не зависит от пути перехода.

Наиболее просто ∆S определяется для обратимых неизолирован­ных изотермических процессов:

∆S = (2.26)

где q — количество теплоты, сообщенное системе.

При изотермическом плавлении или испарении количества ве­щества 1 моль: ∆S = ∆H/T

где ∆H - теплота плавления или теплота испарения.

Если происходит изотермическое расширение п моль идеального газа, то

∆S =nR • 2,3lgV₂/V₁ (2.28)

∆S = nR2,31gp₁/p₂ (2.29)

Если же в системе, состоящей из идеального газа, изменяется одновременно несколько параметров, то

∆S = пС_v . 2,3lgT₂/T₁+ пR • 2,3 lgV₂/V₁ (2.30)

∆S = пС_p • 2,3lgT₂/T₁ + пR ∙2,3lg p₁/p₂ (2.31)

∆S = п • 2,3(C_vlg p₂/p₁ + C_plg(V₂/V₁) (2.32)

Вычисление ∆S в необратимых процессах ведут по уравнениям для процессов обратимых. Это вполне закономерно, так как изме­нение энтропии при заданном начальном и конечном состояниях системы не зависит от пути перехода и, в частности, от обратимости процесса. Если необратимый и обратимый процессы проводятся в одних и тех же граничных условиях, то
∆S_oбр =∆S _неoбр.[2].