Калорические параметры состояния. Обозначение, размерности, физический смысл, P-V диаграмма идеального газа.

К калорическим параметрам состояния относятся следующие основные термодинамические величины: энтропия , внутренняя энергия и энтальпия.

Энтальпия.

В прошлом столетии Гибсс ввел в практику тепловых расчетов новую функцию - энтальпию.

Определение: Энтальпия - это сумма внутренней энергии тела и произведения давления на объем.

I = U + PV

Где:

I - энтальпия; U - внутренней энергия; P - давление; V - объем.

Удельная энтальпия i это отношение энтальпии тела к его массе.

Удельная энтальпия это параметр состояния.

Значение удельной энтальпии пара и воды при определенном давлении и температуре можно найти в справочнике. Пользуясь этими данными, можно определить количество теплоты участвующее в процессе или работу процесса.

Энтропия

Теплота q не является функцией состояния, количество теплоты выделившейся или поглотившейся в процессе зависит от самого процесса. Функцией состояния является энтропия обозначается S размерность Дж/К

dS = dQ/T

где:

dS 0 - дифференциал энтропии; dQ - дифференциал теплоты; Т - абсолютная температура;

Удельная энтропия отношение энтропии тела к его массе. Удельная энтропия s является справочной величиной.

Удельная энтропия - функция состояния вещества, принимающая для каждого его состояния определенное значение:

s = f (Р, v, Т) [Дж/кгЧ к]

Внутренняя энергия единицы массы вещества

называется удельной внутренней энергией (Дж / кг).
Поскольку внутренняя энергия - калорический параметр состояния, ее изменение не зависит от термодинамического пути процесса, а определяется только начальными и конечными состояниями системы

P-V, T-S диаграммы

Характеристики основных видов термодинамических процессов идеальных газов при изменениях таких параметров, как температура, объем, давление и производимая газом работа.

Виды процессов. Основными процессами в технической термодинамике, весьма важными и в теоретическом, и в прикладном отношениях, являются:

изохорный – протекающий при постоянном объеме;

изобарный – протекающий при постоянном давлении;

изотермический – протекающий при постоянной температуре;

адиабатный – при котором отсутствует теплообмен с окружающей средой;

политропный – удовлетворяющий уравнению pvⁿ = const.

Первые четыре процесса являются частными случаями политропного процесса.

При исследовании этих процессов определяют уравнение процесса в координатах p, v и T, s,связь между параметрами состояния газа, измерение внутренней энергии, величину внешней работы и количество отведенной теплоты.

Изохорный процесс. При изохорном процессе выполняется условие dv = 0 или v = const.Из уравнения идеального газа следует, что

p/T = R/v = const

т.е. давление газа прямо пропорционально его абсолютной температуре:

p₂/p₁ = T₂/T₁.

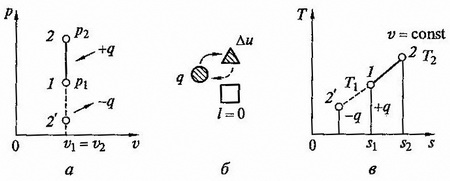
рис. 2.4 Изохорный процесс на p - v и T - s диаграммах (а, в) и схема энергобаланса (б)

Графики процесса на p – v и T – s – диаграммах, а также схема энергобаланса представлены на рисунке. Работа расширения в этом процессе равна нулю, так как dv = 0. Количество теплоты, подведенной к рабочему телу в процессе 1 – 2 при c_v = const, определяется из соотношения

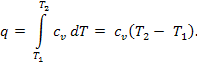
Так как l = 0, то в соответствии с первым законом термодинамики

Δu = q и Δu = c_v(T₂ – T₁) при p = const.

Изобарный процесс. Изобарным называется процесс, происходящий при постоянном давлении. Из уравнения состояния идеального газа при p = const находим

v/T = R/p = const

или

v₂/v₁ = T₂/T₁

т.е. в изобарном процессе объем газа пропорционален его абсолютной температуре (закон Гей-Люссака). Графики процесса на p - v и T – s – диаграммах, а ттакже схема знергобалланса изображены на рис. 2.5.

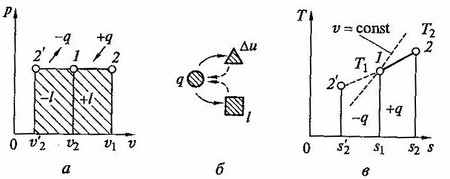
рис.2.5. Изобарный процесс на p - v и T - s - диаграммах (а,в) и схема энергобаланса (б)

Из выражения

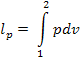
следует, что

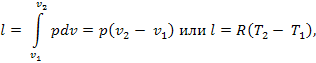
так как pv₁ = RT₁ и pv₂ = RT₂.

Количество теплоты сообщаемое газу при нагревании (или отдаваемое им при охлаждении), находим из уравнения

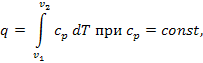
Или

q = c_p(T₂ = T₁).

Изотермический процесс. При изотермическом процессе температура постоянная, следовательно, pv = RT = const или p₂/p₁ = v₁/v₂, т.е. давление и объем обратно пропорциональны друг другу, так что при изотермическом сжатии давление газа возрастает, а при расширении – падает (закон Бойля – Мариотта).

Графиком изотермического процесса в координатах p, v (рис.2.6,а) является равнобокая гипербола, для которой координатные оси служат асимптомами.

Работа процесса

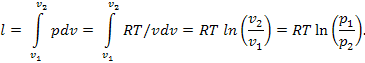
Так как энергия не меняется, то внутренняя энергия идеального газа в данном процессе остается постоянной (Δu = 0) и вся подводимая к газу теплота полностью превращается в работу расширения q = l.

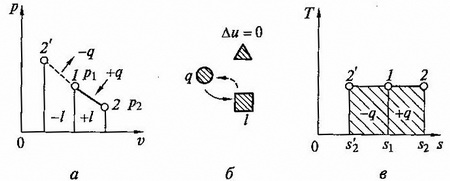
рис. 2.6. Изотермический процесс на p - v и T - s - диаграммах (а,в) и схема энергобаланса (б)

При изотермическом сжатии от газа отводится теплота в количестве, равным затраченной на сжатие работе. Схема энергобаланса и и график изобарного процесса на T – s – диаграмме приведены на рис. 2.6, б,в.

Адиабатный процесс. Адиабатным называется процесс изменения состояния газа, который происходит без теплообмена с окружающей средой. Такой процесс соответствует случаю, когда сосуд или оболочка, вмещающие в себе газ, изолированы в тепловом отношении от окружающей среды. Для данного случая уравнение первого закона термодинамики, поскольку в нем по _{условию dq = 0, принимает вид}

du + pdv = 0

или

Δu + l = 0

Откуда

Δu = -l.

Это означает, что в адиабатном процессе работа расширения совершается только за счет расходования внутренней энергии газа и что при сжатии, происходящем за счет действия внешних сил, вся совершаемая ими работа идет на увеличение внутренней энергии газа.

Обозначим теплоемкость в адиабатном процессе через с_ад и выразим условие du= 0 следующим образом:

du= с_адdT = 0

Это условие говорит о том, что теплоемкость в адиабатном процессе равна нулю, т.е. с_ад = 0. Известно, что

C_p/C_v = k

Уравнение кривой адиабатного процесса (адиабаты) в координатах p, v (рис.2.7 а) имеет вид

pv^k = const,

где k – называется показателем адиабаты (эту величину называют также коэффициентом Пуассона).

Из выражений l = -Δu = c_v(T₁ – T₂) и i₁ – i₂ = c_p(T₁ – T₂) следует, что

i₁ – i₂ = l_техн,

т.е. техническая работа адиабатного процесса расширения равна разности энтальпий начала и конца процесса.

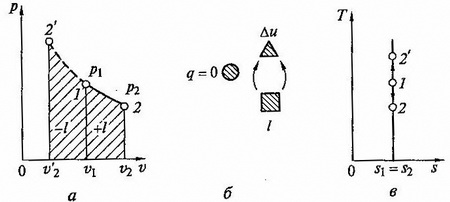
Рис.2.7 Адиабптный процесс на p - v и T - s lиаграммах (а, в) и схема энергобаланса (б)

Адиабатный процесс, происходящий без внутреннего трения в рабочем теле, называется изоэнтропийным. На T – s диаграмме (рис.2.7, в) он изображается вертикальной прямой.

Обычно реальные адиабатные процессы протекают при наличии внутреннего трения в рабочем теле, в результате которого всегда выделяется теплота, которая тут же сообщается самому рабочему телу. В этом случае ds > 0, процесс называется реальным адиабатным процессом.

Политропный процесс и его обобщающее значение. Политропным называется процесс, который происходит при постоянной теплоемкости и описывается уравнением

pvⁿ = const.

Показатель политропы n может принимать любое численное значение в пределах от -∞ до +∞, но для данного процесса он является величиной постоянной.

Из уравнения (2.13) и уравнения Клайперона нетрудно получить выражения, устанавливающие связь между p v и T в любых двух точках на политропе:

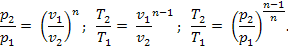
Политропный процесс имеет обобщающее значение, ибо охватывает всю совокупность основных термодинамических процессов.

Певый закон термодинамики

Первый закон термодинамики или закон сохранения энергии для тепловых процессов, связывает количество теплоты, переданное системе, изменение ее внутренней энергии и работу, совершенную системой над окружающими телами.

Одна из возможных его формулировок звучит следующим образом:

Количество теплоты, сообщаемое термодинамической системе, равно сумме изменения ее внутренней энергии ΔU и работы A, совершаемой системой против внешних сил.

Q = ΔU + A.

Если работа совершается внешними силами над термодинамической системой, то, обозначив ее A', первый закон термодинамики можно записать в виде уравнения:

Q + A' = ΔU.

Если термодинамическая система остается изолированной, то есть она не обменивается теплотой с окружающими телами, не совершает работу против внешних сил и внешние силы не совершают работу над системой, то ее внутренняя энергия остается величиной постоянной.

Если A (A') и (или Q) не равны нулю, то следует говорить о сохранении не внутренней энергии термодинамической системы, а внутренней энергии и энергии всех тел, участвующих в термодинамическом процессе.

Если при A = 0 (A' = 0), Q ≠ 0, то теплообмен системы с окружающими телами происходит без превращения внутренней энергии в другие виды.

Если при Q = 0, A ≠ 0 (A' ≠ 0), то происходит превращение одного вида энергии в другой (механической во внутреннюю и внутренней в механическую).

Первый закон термодинамики связывает три величины – ΔU, A (A'), Q.

Изменение внутренней энергии ΔU термодинамической системы не зависит от способа перехода системы из одного состояния в другое, поскольку она по определению является однозначной функцией ее состояния.

В отличие от ΔU, величины A и Q существенно зависят от характера процесса.

Действительно, пусть газ, находящийся в цилиндре под поршнем переходит из состояния А в состояние B тремя разными способами: вдоль изотермы AB, через точку C и через точку D.

В первом случае работа, совершаемая газом, равна площади фигуры, ограниченной изотермой и отрезками BV₂ и AV₁.

Во втором случае работа, совершаемая газом, равна площади прямоугольника p₁(V₂ – V₁).

В третьем случае – площади прямоугольника p₂(V₂ – V₁).

Так как разным переходам соответствуют разные значения работы и одно и то же значение изменения внутренней энергии, то согласно первому закону термодинамики этим переходам будут соответствовать разные количества теплоты.

Из сказанного, в частности, вытекает бессмысленность выражений «запас теплоты», «изменение количества теплоты», «запас работы», «изменение работы». Накопителей работы и теплоты не существует. Работа не приобретается и не расходуется, а совершается в процессе воздействия внешних тел на термодинамическую систему или термодинамической системы на внешние тела. О количестве теплоты или теплообмене можно говорить, только описывая процесс взаимодействия термодинамической системы с внешними телами, в процессе которого происходит изменение ее внутренней энергии. Теплообмен происходит при наличии разности температур участвующих в процессе тел. Результатом теплообмена является выравнивание температур. Таким образом, количество теплоты – это энергия, передаваемая от одного тела другому в процессе теплообмена, а не энергия, которой обладают тела до или после теплообмена.

Первый закон термодинамики является выражением одного из наиболее общих законов природы – закона сохранения и превращения энергии в приложении к определенному и очень распространенному классу физических явлений. Энергия – это универсальная мера движения материи, которая остается постоянной при любых ее превращениях. Закон сохранения энергии говорит о несотворимости и неуничтожимости движения материи. Законы в науке отражают устойчивые, повторяющиеся связи между явлениями. В то же время законы имеют разную степень общности. Закон сохранения энергии относится к разряду наиболее фундаментальных законов природы. Он свидетельствует не только о сохранении материи и ее движения, но и о ее способности к качественным превращениям.