Моделирование потоков жидкости
В формуле (1.5.7) под силой 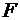 подразумевается одна из основных сил:
подразумевается одна из основных сил:
- сила давления,
- инерции,
- вязкости или тяжести.
Рассмотрим три характерных случая воздействия на движущуюся жидкость основных сил и найдем условия подобия потоков.
1. На жидкость действуют лишь силы давления и инерции, а условием гидродинамического подобия геометрически подобных потоков является равенство для них чисел Эйлера 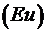 . Физический смысл числа Эйлера - это величина, пропорциональная отношению сил давления
. Физический смысл числа Эйлера - это величина, пропорциональная отношению сил давления 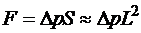 к силам инерции
к силам инерции 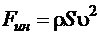 , тогда
, тогда
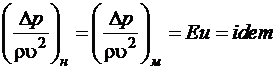 , (1.5.8)
, (1.5.8)
где 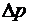 - разность давлений или просто давление.
- разность давлений или просто давление.
2. На жидкость действуют силы вязкости, давления и инерции, а условием гидродинамического подобия геометрически подобных потоков является равенство чисел Рейнольдса 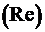 , подсчитанных для сходных сечений потоков. Физический смысл числа Рейнольдса - это величина, пропорциональная отношению сил вязкости
, подсчитанных для сходных сечений потоков. Физический смысл числа Рейнольдса - это величина, пропорциональная отношению сил вязкости 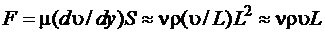 к силам инерции
к силам инерции 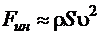 , тогда
, тогда
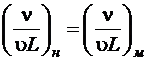 или
или 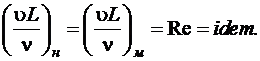 (1.5.9)
(1.5.9)
3. На жидкость действуют силы тяжести, давления и инерции, а условием гидродинамического подобия геометрически подобных потоков является равенство чисел Фруда 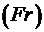 .
.
Физический смысл числа Фруда - это величина, пропорциональная отношению сил инерции 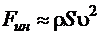 к силам тяжести
к силам тяжести 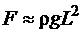 , тогда
, тогда
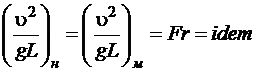 . (1.5.10)
. (1.5.10)
Для промышленной гидравлики наиболее важным является число Рейнольдса, так как им определяется основной критерий подобия напорных потоков. За характерный линейный размер 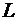 при подсчете числа Рейнольдса должен приниматься поперечный размер потока, например, диаметр сечения.
при подсчете числа Рейнольдса должен приниматься поперечный размер потока, например, диаметр сечения.
Гидравлическим радиусом(R) принято обозначать соотношение площади живого сечения к смоченному периметру. Так, к примеру, для круглой трубы, работающей полным сечением, гидравлический радиус равен одной четвертой ее диаметра. Формула принимает вид:
R = w / χ = πd2 / 4 πd = d / 4.
Живым сечение (w) принято обозначать поперечное сечение потока, перпендикулярное ко всем без исключения линиям тока.
К примеру, при рассмотрении круглой трубки с диаметром d, причем все поперечное сечение заполнено жидкостью, живое сечение представлено площадью круга:
w =πd2 / 4 , м2.
Смоченный периметр(χ) – та часть периметра живого сечения, которая граничит с твердыми стенками, формируя смоченную поверхность. К примеру, для русла вся боковая поверхность потока, без свободной плоскости, там, где жидкость граничит с газообразной средой.
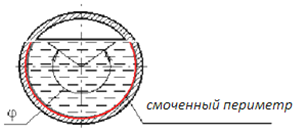
Для круглой трубы, работающей полным сечением, смоченный периметр будет равняться длине окружности, значит формула примет вид:
χ = πd, м.
Для круглой незаполненной трубы формула принимает вид:
когда угол в радианах,
χ = πdφ / 3600
или когда угол φ в градусах
χ = πdφ / 2π = πdφ / 2π.
Гидравлическим диаметром (D) принято обозначать соотношение учетверенной площади живого сечения к смоченному периметру:
D = 4w / χ.
Установим общую зависимость между скоростями в потоке жидкости, для которого соблюдается условие сплошности, или неразрывно с т и, движения, т. е. не образуется пустот, не заполненных жидкостью.
Выделим внутри потока элементарный параллелепипед объемом 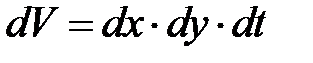 , ребра которого ориентированы параллельно осям координат (рис. 5).
, ребра которого ориентированы параллельно осям координат (рис. 5).
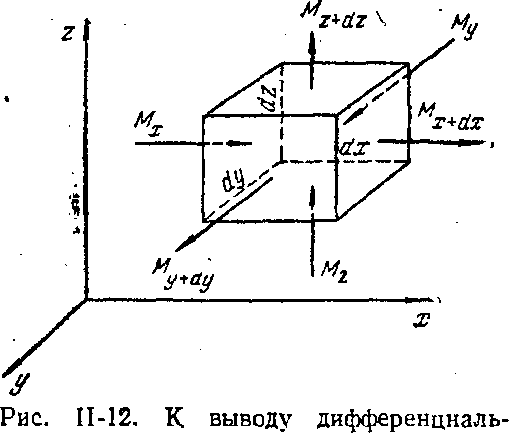
Рис. 5 К Выводу уравнения неразрывности потока
Пусть составляющая скорости потока вдоль оси х в точках, лежащих на левой грани параллелепипеда площадью 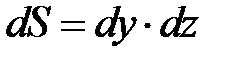 , равна
, равна 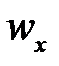 . Тогда, согласно уравнению (4-1), через эту грань в параллелепипед войдет вдоль оси
. Тогда, согласно уравнению (4-1), через эту грань в параллелепипед войдет вдоль оси 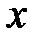 за единицу времени масса жидкости
за единицу времени масса жидкости 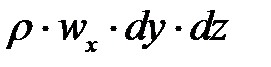 pwxdydz, а за промежуток времени
pwxdydz, а за промежуток времени 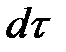 – масса жидкости
– масса жидкости 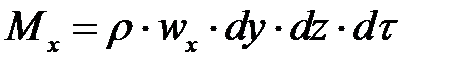
где 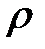 – плотность жидкости на левой грани параллелепипеда.
– плотность жидкости на левой грани параллелепипеда.
На противоположной (правой) грани параллелепипеда скорость и плотность жидкости могут отличаться от соответствующих величин на левой грани и будут равны
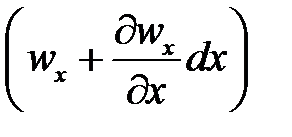 и
и 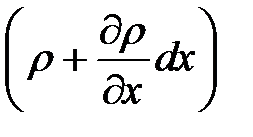
Тогда через правую грань параллелепипеда за то же время 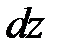 выйдет масса жидкости
выйдет масса жидкости
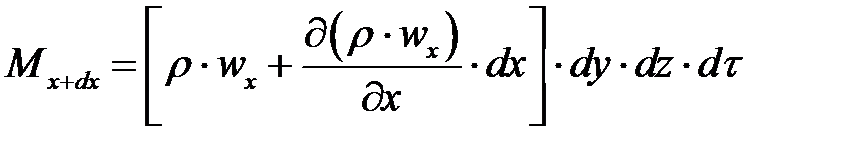
Приращение массы жидкости в параллелепипеде вдоль оси 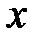 :
:
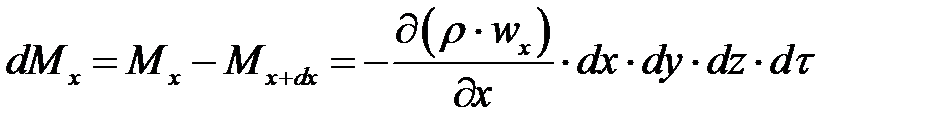
Если составляющие скорости вдоль осей 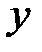 и
и 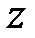 равны
равны 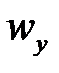 и
и 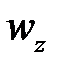 соответственно, то приращения массы в элементарном объеме вдоль этих осей по аналогии составят:
соответственно, то приращения массы в элементарном объеме вдоль этих осей по аналогии составят:
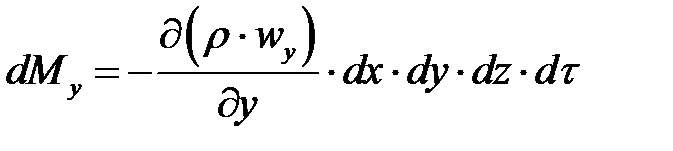
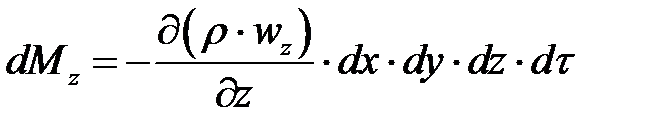
Общее накопление массы жидкости в параллелепипеде за время dr равно сумме ее приращений вдоль всех осей координат:
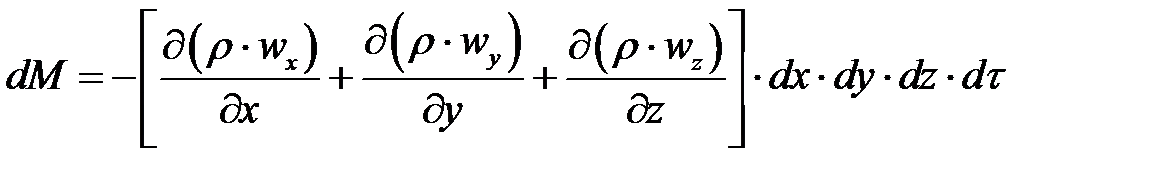
Вместе с тем изменение массы в полностью заполненном жидкостью объеме параллелепипеда возможно только вследствие изменения плотности жидкости в этом объеме. Поэтому
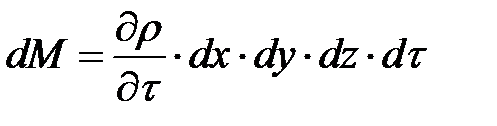
Приравнивая оба выражения:
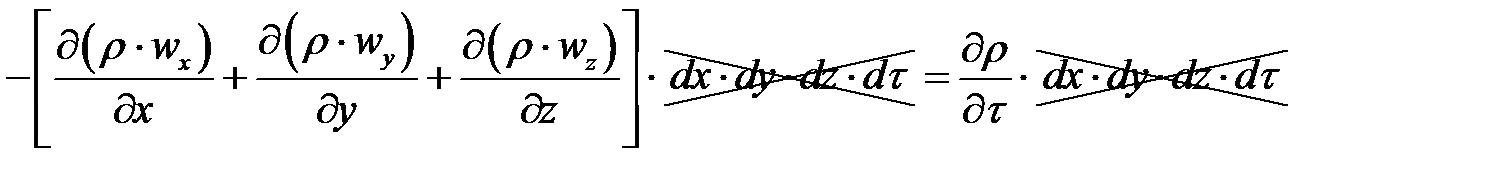
окончательно получим:
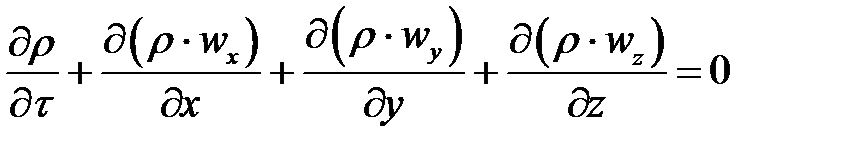 | 4-14 |
Данное уравнение представляет собой дифференциальное уравнение неразрывности патока для неустановившегося движения сжимаемой жидкости.
Уравнение (4-14) может быть записано и в несколько иной форме. Проводя дифференцирование произведений 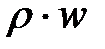 , получим
, получим
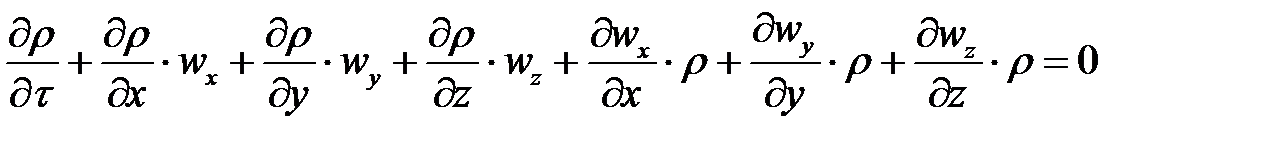
или
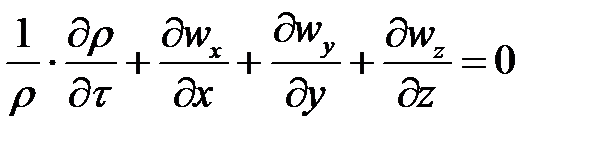 | 4-14а |
В установившемся потоке плотность не изменяется во времени, т. е. 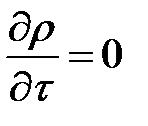 , и уравнение (4-14) принимает вид
, и уравнение (4-14) принимает вид
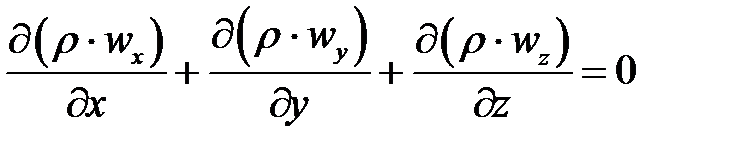 | 4-15 |
Для капельных жидкостей, которые практически несжимаемы, а также для газов в условиях изотермического потока при скоростях, значительно меньших скорости звука, 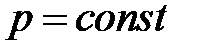 и, следовательно
и, следовательно
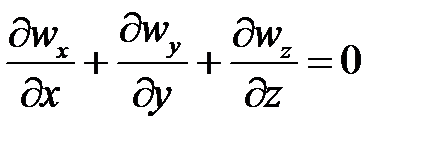 | 4-16 |
Уравнение (4-15) является дифференциальным уравнением неразрывности потока несжимаемой жидкости.
Сумма изменений скорости вдоль осей координат в левой части уравнения (4-15) называется дивергенцией вектора скорости и обозначается через 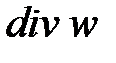 . Поэтому данное уравнение можно представить как
. Поэтому данное уравнение можно представить как
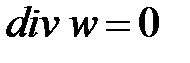 | 4-16а |
Для того чтобы перейти от элементарного объема ко всему объему жидкости, движущейся сплошным потоком (без разрывов и пустот) по трубопроводу переменного сечения (рис. 6), проинтегрируем дифференциальное уравнение (4-15).
1. Уравнение Бернулли для струйки идеальной жидкости
