Основы теории гидравлического подобия

Дифференциальные уравнения движения жидкости интегрируются лишь для сравнительно небольшого числа простейших случаев. Поэтому для решения большинства сложных инженерных задач в гидравлике приходится использовать экспериментальные исследования. Эксперименты проводят в лабораторных условиях на моделях, выполняемых, как правило, в меньшем масштабе, чем натурные образцы, что приводит к значительной экономии всех ресурсов. Эти исследования дают возможность выявить на модели гидравлическую картину работы устройства и при наличии недостатков в его работе устранить их. Исследования на моделях позволяют также вносить коррективы в формулы, полученные теоретически, а также устанавливать эмпирические (опытные) зависимости между отдельными элементами изучаемого явления. Для переноса результатов исследований моделей на натурные образцы необходимо, чтобы модель была подобна натуре, а для этого нужно знать условия подобия, определяющие подобие между явлениями, происходящими в модели и в натуре. Эти условия подробно рассматриваются в теории подобия.

В гидравлике широко используют моделирование явлений, основой которого служит, теория гидродинамического подобия, то есть подобия потоков несжимаемой жидкости.

Гидродинамическое подобие складывается из подобий:

• геометрического,
• кинематического,
• динамического .

Геометрическое подобие представляет собой пропорциональность сходных размеров и равенство соответствующих углов. Отношение двух сходных размеров подобных потоков называют линейным масштабом 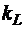. Эта величина одинакова 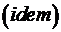для подобных потоков, то есть

,

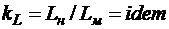где 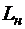- размер в натуре,

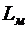- размер на модели.

Кинематическое подобие означает пропорциональность местных скоростей в сходных точках и равенство углов, характеризующих направление этих скоростей:

,

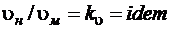где 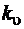- масштаб скоростей.

Для кинематического подобия требуется геометрическое подобие трубопроводов (потоков).

Динамическое подобие предусматривает пропорциональность сил, действующих на сходные объемы в потоках, имеющих кинематическое подобие, и равенство углов, характеризующих направление этих сил.

В потоках жидкостей обычно действуют разные силы:

• силы давления,
• вязкости (трения),
• тяжести и др.

Соблюдение их пропорциональности означает полное гидродинамическое подобие.

Осуществление на практике полного гидродинамического подобия весьма затруднительно, поэтому обычно рассматривают частичное (неполное) подобие, при котором соблюдается пропорциональность лишь основных, главных для данного случая сил.

Для напорных течений потоков в трубах, в гидравлических машинах, устройствах и аппаратах, такими силами, как показывает анализ, являются силы давления, вязкости и силы инерции. На жидкость действует также сила тяжести, но в напорных потоках ее действие сводится к соответствующему изменению давления. Поэтому, рассматривая так называемое приведенное давление 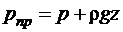, тем самым учитывают силу тяжести.

Общая теория динамического подобия базируется на втором законе Ньютона. Для того чтобы на модели сообщить частице жидкости массой 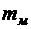ускорение 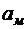, к ней нужно приложить силу

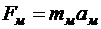. (1.5.2)

Зная, что масса равна произведению плотности 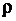на объем 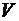, можно записать

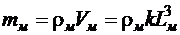, (1.5.3)

где 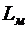- один из характерных размеров модели;

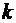- коэффициент пропорциональности, зависящий от геометрической формы рассматриваемой частицы жидкости.

Ускорение

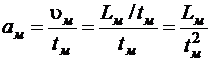, (1.5.4)

где 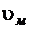- скорость частицы жидкости на модели;

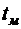- отрезок времени, за который частица жидкости приобрела ускорение .

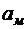После подстановки в формулу (1.5.2) выражений (1.5.3) и (1.5.4) получим

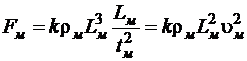. (1.5.5)

Аналогичное выражение для силы 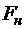, приложенной к частице жидкости в натуре, будет иметь вид

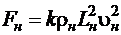. (1.5.6)

Отношение между соответствующими силами для натуры и модели определяется зависимостью

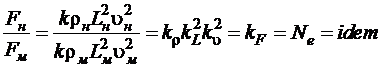, (1.5.7)

где 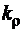- масштаб плотностей;

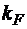- масштаб сил.

Зависимость (1.5.7) выражает общий закон подобия Ньютона, который формулируется следующим образом: в динамически подобных процессах отношение между двумя соответствующими силами, действующими в натуре и на модели, одинаково, называется числом Ньютона и обозначается 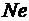.