Лекция №1 Линейные электрические цепи постоянного тока
Уравнения цепи
Независимые узлы и уравнения по закону Кирхгофа для токов
| R |
| I |
| UE |
| E1 |
| R1 |
| R2 |
| R3 |
| R4 |
| R5 |
Главные контуры и уравнения по закону Кирхгофа для напряжений
| R6 |
| E4 |
| 3к |
| 2 |
| 1 |
| 3 |
| 1к |
| 2к |
| 5 |
| E1 |
| R1 |
| R2 |
| R3 |
| R4 |
Уравнения элементов
| R5 |
| R6 |
| E4 |
| 2 |
| 3 |
| 4 |
Число ветвей «в»: в = 6
Число узлов «у»: у = 4
| 1 |
| E1 |
| R1 |
| R2 |
| R3 |
| R4 |
| R5 |
| R6 |
| E4 |
| I1 |
| I4 |
Система из «в» уравнений (в = 6)
Лекция № 4 Трёхфазные цепи
1. Трёхфазная система ЭДС
2. Соединение обмоток генератора звездой
3. Соединение обмоток генератора треугольником
4. Соединение потребителей звездой
5. Соединение потребителей треугольником
6. Мощность трёхфазного тока
7. Вращающееся магнитное поле
1. Трёхфазная система ЭДС
Трёхфазной называется система трёх ЭДС одинаковой частоты, сдвинутых друг относительно друга по фазе так, что сумма углов сдвига фаз равна 2π, или 3600.
Трёхфазная система ЭДС называется симметричной, если ЭДС трёх фаз сдвинуты друг относительно друга на угол 2π/3 = 1200 и амплитуды этих трёх ЭДС одинаковы по величине:
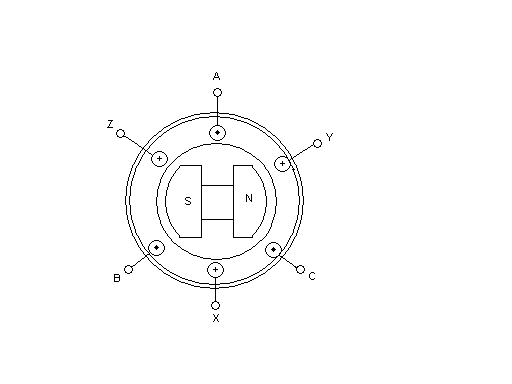
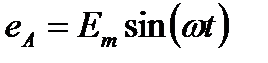
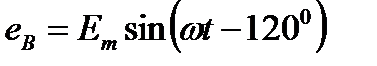
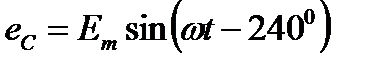
Получение симметрично трёхфазной системы ЭДС осуществляется в электромашинном генераторе, в котором три жёстко скреплённые под углом 1200 обмотки пересекают магнитное поле с частотой ω.
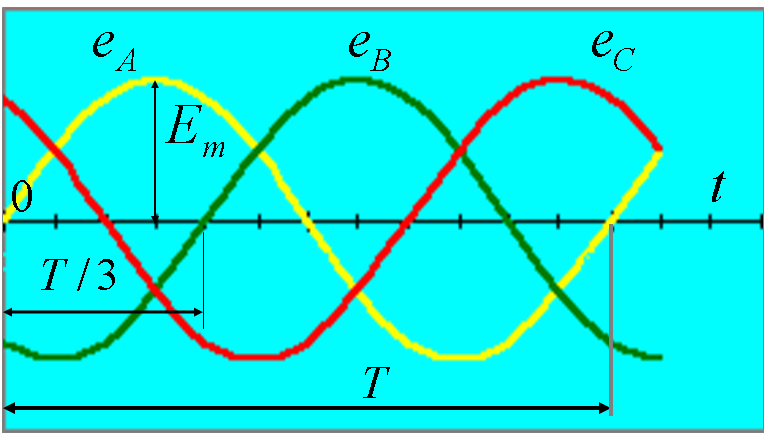
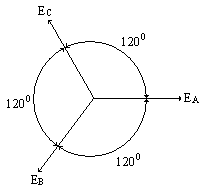
К каждой обмотке генератора может быть подключена нагрузка. Три обмотки генератора соединяются друг с другом электрически. Такая трёхфазная система называется связанной.
Каждая обмотка генератора со своей нагрузкой и соединительными проводами называется фазой.
В трёхфазной система энергоснабжения фазы обозначают прописными буквами А, В, С.
2. Соединение обмоток генератора звездой
При соединении обмоток генератора звездой концы обмоток X, Y, Z электрически соединяются. Эта точка соединения называется нулевой (нейтральной) и обозначается 0.
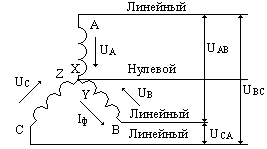
Фазным называется напряжение между началом и концом обмотки генератора или между нулевым и линейным проводом.
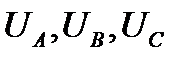Обозначаются фазные напряжения прописными буквами с индексами фаз
Линейным называется напряжение между началами обмоток генератора или между линейными проводами.
Обозначаются линейные напряжения прописными буквами с индексами фаз
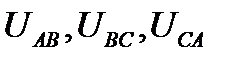
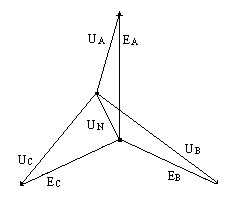
При соединении обмоток генератора звездой действующее линейное напряжение определяется геометрической разностью двух соответствующих фазных напряжений.
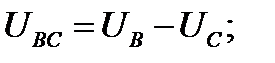
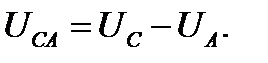
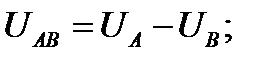
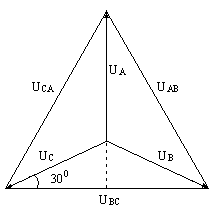
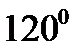
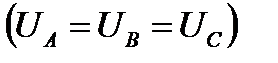При симметричной системе ЭДС фазные напряжения равны по величине
и сдвинуты на
Определим линейное напряжение по векторной диаграмме
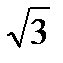
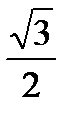
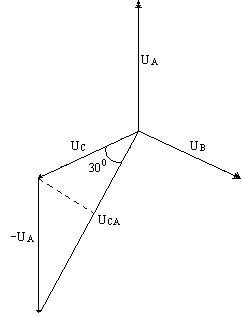
UCA = 2 UC cos300 = 2 UC = UC
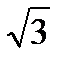
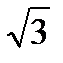При симметричной системе ЭДС линейное напряжение трёхфазного генератора, обмотки которого соединены звездой, в= 1,73 раза больше фазного напряжения:Uл =Uф
В связанных трёхфазных системах фазным называется ток, проходящий по обмотке (фазе) генератора Iф, а линейным считается ток, проходящий по линейному проводу Iл.
При соединении обмоток генератора звездой линейный ток Iл равен фазному току Iф:
Iл = Iф.
3. Соединение обмоток генератора треугольником
При соединении обмоток генератора треугольником
конец обмотки фазы А соединяется с началом обмотки фазы В,
конец обмотки фазы В соединяется с началом обмотки фазы С,
конец обмотки фазы С соединяется с началом обмотки фазы А и к точкам соединения подключаются линейные провода.
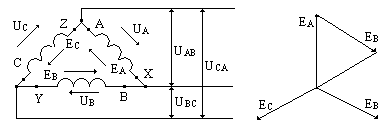
При соединении обмоток генератора треугольником трёхфазная цепь трёхпроводная.
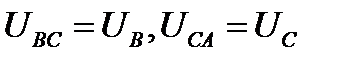
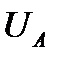
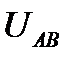Из схемы соединения обмоток треугольником следует, что линейное напряжениеравно фазному напряжению ,
т.е.
Uл = Uф.
При симметричной системе ЭДС и правильном соединении обмоток генератора треугольником геометрическая сумма ЭДС обмоток генератора, образующих замкнутый контур, равна нулю. Следовательно, и ток в замкнутом контуре обмоток, соединенных треугольником, также равен нулю при холостом ходе независимо от внутреннего сопротивления обмоток.
Если обмотки симметричного генератора соединены «неправильным» треугольником, т.е. неправильно подключить начало и конец хотя бы одной из обмоток, то геометрическая сумма ЭДС в замкнутом контуре обмоток будет равна удвоенному значению ЭДС одной фазы. С учётом малого внутреннего сопротивления обмоток генератора ток в замкнутом контуре достигает катастрофической величины даже при отсутствии нагрузки (холостой ход), что равносильно короткому замыканию в замкнутом контуре обмоток.
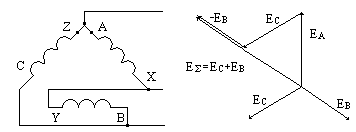
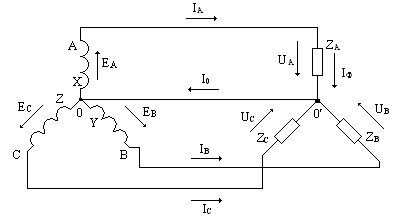
4. Соединение потребителей звездой
При соединении звездой потребителя и генератора трёхфазная система представляет собой сложную цепь с двумя узловыми точками .
Соединение генератора и потребителя с нулевым проводом представляет собой четырёхпроводную схему. При этом потенциалы узловых точек одинаковы, и если сопротивления фаз одинаковы по величине
ZA = ZB = ZC
и имеют одинаковый угол сдвига фаз
φА = φВ = φС,
то такую нагрузку, подключенную к трёхфазному генератору, считают симметричной.
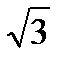Величина напряжения на каждой фазе потребителя, соединенного звездой, в
= 1,73 раза меньше линейного напряжения, т.е.
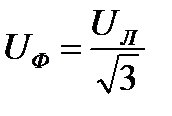
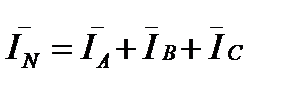Ток в нулевом проводе при соединении потребителей звездой определяется геометрической суммой токов в фазах потребителя:
Токи в фазах потребителя определяются по формулам
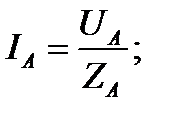
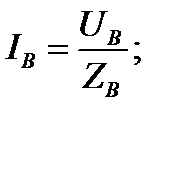
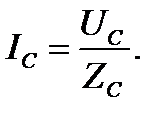
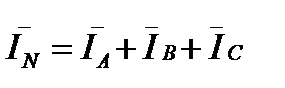Очевидно, при равномерной нагрузке фаз UA = UB = UC и ZA = ZB = ZC токи в фазах равны по величине и сдвинуты, как и напряжения, по фазе на 1200. Следовательно, их геометрическая сумма
равна нулю, т.е. ток в нейтральном проводе отсутствует.
При неравномерной (несимметричной) нагрузке фаз отсутствие нулевого провода приводит к неодинаковым по величине напряжениям на каждой фазе потребителя. При этом на фазе с большим сопротивлением будет и большее напряжения.
Т.к. отсутствие нулевого провода при неравномерной нагрузке фаз потребителя, соединенного звездой, нарушает режим работы потребителей, то предохранитель в нулевом проводе не ставят.
Следовательно, нулевой провод служит для выравнивания напряжений на фазах потребителя при неравномерной нагрузке фаз.
При соединении потребителя звездой ток каждой фазы потребителя равен линейному току трёхфазной цепи:
IФ = IЛ.
5. Соединение потребителей треугольником
При соединении потребителя треугольником к каждой фазе потребителя приложено напряжение трёхфазной цепи
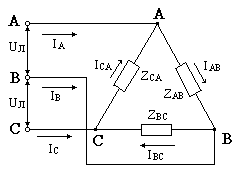
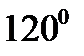Т.к. при симметричной ЭДС все линейные напряжения равны по величине и сдвинуты на угол по фазе, то и напряжения на каждой фазе потребителя, соединенного треугольником, равны по величине
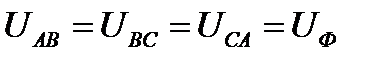
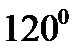
и сдвинуты по фазе на угол независимо от нагрузки.
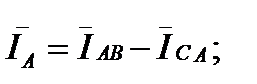
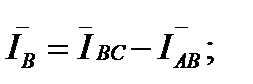
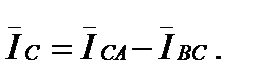В соответствии с первым законом Кирхгофа линейные токи можно определить выражениями:
Линейный ток при соединении потребителей треугольником определяется геометрической разностью двух фазных токов, сходящихся с линейным в одной узловой точке.
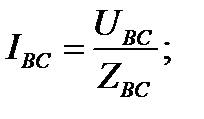Фазные токи потребителя, соединенного треугольником, определяются
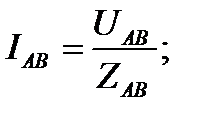
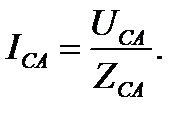
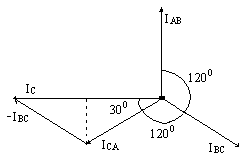
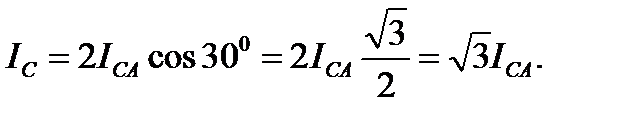При симметричной системе ЭДС генератора () и равномерной нагрузке фаз потребителя () токи в фазах потребителя равны между собой по величине () и также как напряжения на фазах потребителя сдвинуты друг относительно друга по фазе на угол 1200.
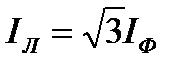Таким образом, при равномерной нагрузке фаз и симметричной системе ЭДС при соединении потребителей треугольником линейный ток в трёхфазной цепи в = 1,73 раза больше фазного тока.
6. Мощность трёхфазного тока
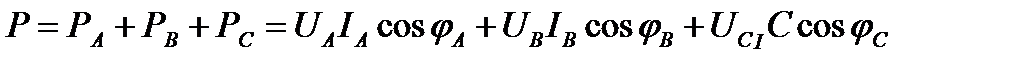Активная мощность, отдаваемая трёхфазным генератором и потребляемая трёхфазным потребителем, определяется суммой активных мощностей каждой фазы потребителя:
Аналогично для реактивной мощности трёхфазного тока:
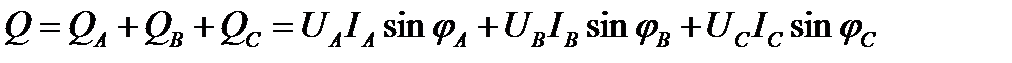
Полная мощность трёхфазного потребителя
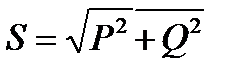
На практике удобнее оперировать линейными величинами, т.к. доступными являются линейные провода, а не обмотки генератора или двигателя.
При соединении потребителя звездой при равномерной нагрузке фаз
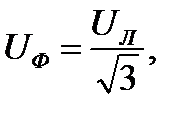
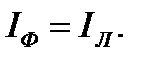
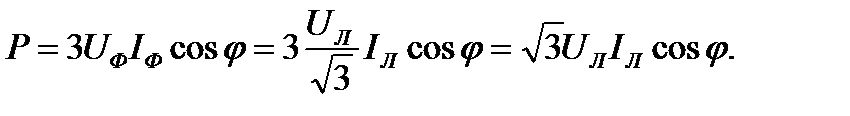Тогда
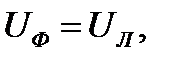
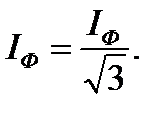При соединении потребителей треугольником при равномерной нагрузке фаз
а
Тогда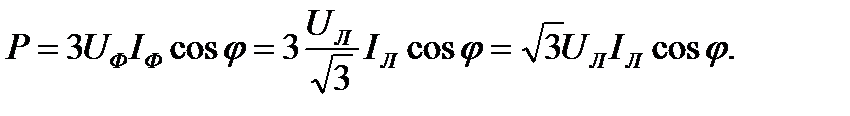 
Т.о., при равномерной нагрузке фаз при соединении потребителей звездой и треугольником мощности трёхфазного тока определяются выражениями:
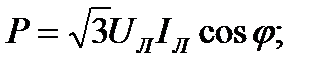
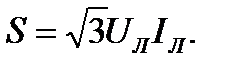
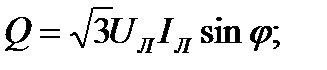
Лекция № 5 Магнитные цепи
1. Основные определения и параметры
2. Анализ и расчёт магнитных цепей
1. Основные определения и параметры
Неразрывность электрического и магнитного полей
В природе существует единое электромагнитное поле, а чисто электрическое и чисто магнитное поля являются лишь его частными случаями.
Магнитное поле во всех без исключения случаях создаётся движущимися зарядами (в т. ч. вращающимися вокруг атомов и смещающимися в диэлектрике) или токами
Изменяющиеся электрическое и магнитное поля индуктируют друг друга.
Магнитное поле - вид материи, характеризующийся воздействием на движущиеся электрически заряженные частицы с силой, пропорциональной заряду этой частицы и её скорости.
Магнитное поле в пустоте, воздухе и других немагнитных средах определяется во всех точках векторами магнитной индукция В (магнитного потока Ф ) и напряжённости магнитного поля Н , а в ферромагнитных материалах - векторами индукции В , напряженности М и намагниченности
Магнитная индукция
Магнитная индукция В - векторная величина, определяющая силу, действующую на движущуюся заряженную частицу со стороны магнитного поля в данной его точке. Магнитная индукция численно равна отношению силы FC , действующей на заряженную частицу, к произведению заряда q и составляющей скорости частицы, перпендикулярной к вектору силы, т. е.
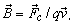
Единица магнитной индукции
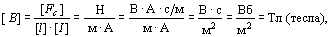
т. е. магнитная индукция 1 Тл равна силе, действующей на 1 м длины проводника с током в 1 А.
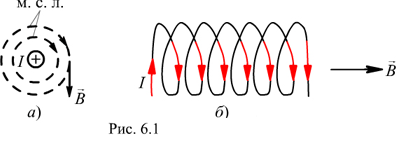
Изображение магнитного поля и направление магнитной индукции
Графически магнитное поле принято изображать с помощью магнитных силовых линий (м. с. л.), которые проводят так, чтобы касательные к ним определяли направления векторов магнитной индукции, а плотность линий была пропорциональна длине этих векторов.
При этом условно положительное направление м. с. л. вокруг проводника с током (рис. 6.1, а) связано с направлением тока в проводнике правилом правоходового винта; направление магнитной индукции должно совпадать с направлением касательной к магнитным силовым линиям
Магнитный поток и потокосцепление
| Ф = ВSм |
Единица магнитного потока: [Ф] = [B][S] = Tлм2 = Вб (вебер).
При протекании тока в катушке, магнитный поток несколько раз сцепляется с витками катушки. В первом приближении можно считать, что все линии магнитной индукции сцепляются со всеми витками w катушки. Тогда потокосцепление катушки связывается с потоком Ф простым соотношением:
Ψ = wФ.
Напряжённость магнитного поля
Физический смысл вектора Н определяется законом Био-Савара: элемент тока Idlсоздаёт в точке, находящейся на расстоянии R от элемента тока (рис. 6.2), магнитное поле с напряжённостью
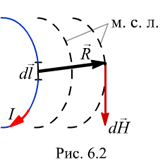
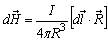
Единица измерения напряжённости магнитного поля (ампер на метр).
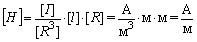
Зависимость В от Н принято записывать в виде
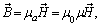
Намагниченность ферромагнетиков
К ферромагнитным материалам (сокращённо ферромагнетикам) относят сплавы на основе железа, никеля, кобальта и других редкоземельных элементов, их соединения; сплавы и соединения марганца, хрома, а также пластические и другие композиции с включением порошков ферромагнитных металлов (ферриты).
Свойства ферромагнитных материалов определяются значением абсолютной магнитной проницаемости
Наиболее распространённые ферромагнетики – это сплавы на основе железа с добавками Ni, Co, или на основе кобальта (Co) с крупнозернистой структурой (с зернами-доменами размером 10-3 нм и объёмом 10-9...10-10 нм3) и с относительной магнитной проницаемостью m = ma/m0 = 500...5000 и более.
При отсутствии магнитного поля самопроизвольная намагниченность доменов ориентирована хаотически и результирующее магнитное поле, образованное намагниченностью этих доменов, слабое (В » 0). Под действием внешнего магнитного поля наблюдается принудительная ориентация намагниченности доменов по направлению внешнего магнитного поля и усиление результирующего магнитного потока.
Можно предположить, что при каком-то большом внешнем поле получим одинаковую ориентацию намагниченности всех доменов (или большинства из них), и дальнейшего усиления внешнего магнитного потока Ф и индукции В = Ф/S не будет. Это явление называют насыщением ферромагнитного материала.
Кривые намагничивания
Для оценки свойств ферромагнетиков строят кривые намагничивания В = f(Н), приводимые в справочниках. С их помощью можно для каждого значения напряжённости поля Н определить значение магнитной проницаемости μa, которая при возрастании напряжённости поля сначала увеличивается, затем уменьшается
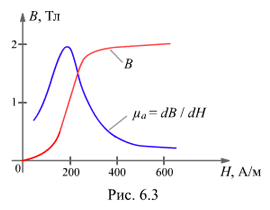
Петля гистерезиса
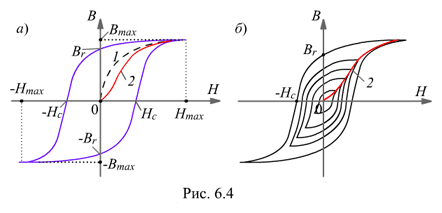
Классы ферромагнитных материалов
магнитно-мягкие материалы с узкой круто поднимающейся петлёй гистерезиса с Hc<200 А/м (рис. 6.5, кривая 1). Их используют в трансформаторах, асинхронных двигателях и других устройствах переменного тока, т. е. там, где требуется иметь малые потери при перемагничивании – в магнитопроводах с большими переменными индукциями
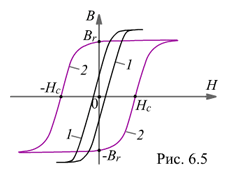
К магнитно-мягким материалам относится электротехническая сталь, технически чистое железо, литая сталь и др.;
- магнитно-твердые материалы с коэрцитивной силой Hc>4000 А/м (рис. 6.5, кривая 2). Их применяют для изготовления постоянных магнитов, которые должны иметь большие значения Hc. К ним относятся литые сплавы на основе Fe-Co-Ni-Al типа ЮНДК, бариевые сплавы (марки БИ), металлокерамические сплавы (ММК), сплавы кобальта с самарием, гадолинием и др.;
- специальные магнитные материалы, характеризуемые либо особой формой петли гистерезиса, например, прямоугольной (ферриты марки Вт и др.), либо специфическими свойствами: с сильной зависимостью магнитных свойств от температуры (сплавы никеля с медью марки Н38Х14 и др.); со значительными изменениями геометрических размеров при перемагничивании (магнитострикционные материалы из сплава железа с 14% алюминия и никеля или из сплава железа и кобальта марок НП-2-Т, 50КФ, 14НЮ); железокобальтовые сплавы - пермендюр с максимальной индукцией насыщения до 2,4 Тл; пермаллои (сплавы железа с никелем и добавками других металлов марок 79НМ, 80НХС и др.), имеющие большую магнитную проницаемость в слабых магнитных полях, и др.
Назначение и типы магнитных цепей
В устройство многих ЭТ устройств входят магнитные цепи,
● сосредоточить магнитное поле в определённом объёме;
●уменьшить намагничивающую силу и мощность намагничивающей катушки при заданном значении магнитной индукции (или потока).
Магнитная цепь - это совокупность устройств, содержащих ферромагнитные тела, электромагнитные процессы в которых могут быть описаны с помощью понятий магнитодвижущей силы, магнитного потока и разности магнитных потенциалов.
В состав магнитной цепи входят
● магнитопровод из ферромагнитного материала,
● намагничивающая катушка,
● воздушный зазор.
Различают:
- магнитные цепи с постоянными магнитами;
- магнитные цепи, в которых магнитный поток создается постоянным или переменным током, протекающим в одной или нескольких обмотках, размещённых на ферромагнитных сердечниках
Назначение ферромагнитного сердечника
Намагничивающими катушками различных устройств создается магнитное поле во всем окружающем пространстве.
Однако магнитная индукция вне магнитной цепи из ферромагнитного материала получается значительно меньше.
Поэтому во многих случаях можно считать, что практически всё магнитное поле сосредоточено в магнитной цепи из ферромагнитного материала. Придавая магнитной цепи соответствующую конфигурацию и размеры,
можно сосредоточить магнитное поле в требуемом объёме.
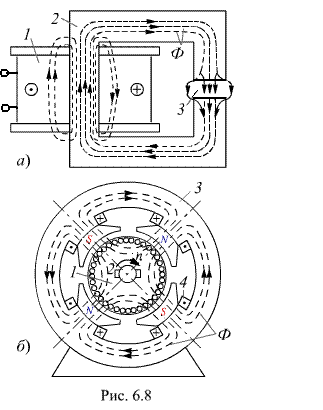
Обычно в электромагнитных устройствах стремятся на пути магнитного потока разместить ферромагнитные материалы 2, чтобы уменьшить величину тока намагничивающей обмотки 1 (рис. 6.8, а). Однако между частями магнитопровода неизбежны воздушные зазоры (рис. 6.8, б), или магнитопровод специально изготавливают с регулируемым зазором 3
В низкочастотных устройствах (f < 1000 Гц) катушки размещают на ферромагнитных сердечниках, что приводит к многократному усилению магнитных потоков и их концентрации в самом ферромагнитном материале, и, как следствие, создается нужная конфигурация магнитного поля и магнитной цепи.
Если вся магнитная цепь выполнена из одного ферромагнитного материала и имеет одинаковое сечение, то она называется однородной.
Магнитная цепь, содержащая материалы с различными магнитными свойствами или имеющая воздушные зазоры, называется неоднородной.
Магнитная цепь, во всех сечениях которой магнитный поток Ф одинаков, называется неразветвлённой.
В разветвлённой магнитной цепи потоки на различных участках неодинаковы
Магнитные поля различных ЭТ устройств возбуждаются в большинстве случаев с помощью намагничивающих катушек.
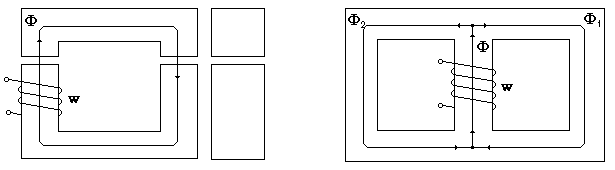
Характерной особенностью неразветвлённой магнитной цепи является то, что магнитный поток Ф, созданный токами обмоток, для всех участков и сечений цепи имеет одинаковое значение.
Разветвленные магнитные цепи бывают
симметричные и несимметричные.
Симметричной считается магнитная цепь,
● ветви которой расположены по обе стороны от линии, проведённой через узловые точки разветвления магнитных потоков,
● выполнены из одних материалов и
● имеют одинаковые геометрические размеры.
Дополнительным условием симметрии является равенство их намагничивающих сил.
Магнитное поле создается электрическим током и неразрывно связано с ним, поэтому необходимо установить зависимость напряженности магнитного поля от силы тока.
Эта зависимость устанавливается законом полного тока. Если напряжённость магнитного поля имеет одинаковую величину по всему контуру и направлена по магнитной линии, то уравнение закона полного тока имеет вид:
Hl = ∑I
где ∑I – полный ток;
Hl – намагничивающая сила
Полный ток катушки, имеющей w витков равен произведению Iw. Тогда формула, выражающая закон полного тока будет иметь вид
Hl = Iw
Расчет магнитных цепей
При анализе и расчёте магнитных цепей приходится решать две основные задачи:
прямую задачу (наиболее часто встречается);
обратную задачу.
Прямой считается такая задача, когда известной величиной является магнитный поток или магнитная индукция какого-либо участка магнитной цепи, а определению подлежит намагничивающаяся сила или ток катушки.
При решении обратной задачи намагничивающая сила или ток катушки считаются известными, а подлежит определению магнитный поток или магнитная индукция
Закон Ома для магнитных цепей
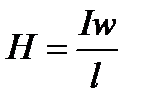Из формулы, представляющей закон полного тока, следует
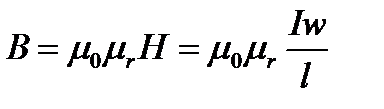Поскольку
то магнитный поток для однородной магнитной цепи определиться
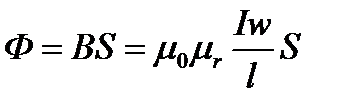
Отсюда можно получить выражение для
● магнитодвижущей силы или магнитного сопротивления
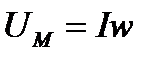
и
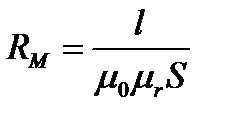● магнитного сопротивления
Тогда магнитный поток магнитной цепи выразится
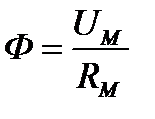
Это и есть математическое выражение закона Ома для неразветвлённой однородной магнитной цепи: магнитный поток в рассматриваемой магнитной цепи пропорционален магнитному напряжению UM и обратно пропорционален магнитному сопротивлению RM.
Если неразветвлённая цепь неоднородна и на сердечнике имеются две обмотки, то закон Ома для магнитной цепи, состоящей из трёх однородных участков:
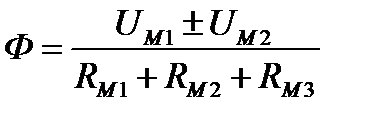
Знак «+» между магнитными напряжениями ставится, когда обмотки включены «согласно», т.е. создают магнитные потоки в сердечнике одного направления.
Знак «-» ставится, когда обмотки включены «встречно», т.е. создают магнитные потоки в сердечнике, направленные друг против друга.
1.Анализ и расчёт магнитных цепей
Расчёт неразветвленных магнитных цепей
При расчёте неразветвлённой магнитной цепи различают т. н. прямую задачу (задачу синтеза) и обратную (задачу анализа магнитной цепи).
Прямая задача
Заданы геометрические размеры магнитной цепи (lM, d, S1, рис. 6,15, а) и магнитные свойства отдельных её участков - кривые намагничивания В(Н) (рис. 6.15, б), например, все они изготовлены из электротехнической стали 1411. Нужно определить магнитодвижущую силу (МДС) F обмотки, необходимую для создания магнитного потока Ф в зазоре
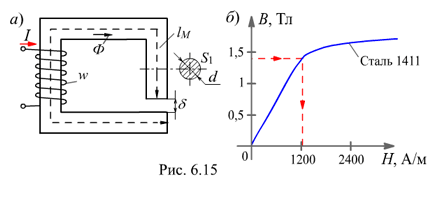
Примем S1 =S2 и определим магнитную индукцию на участках цепи:
B1 = Ф / S1; Bδ= Ф / Sδ ; B1 = Bδ.
Напряжённость магнитного поля на участке lM найдем по кривой намагничивания; например, для стали 1411 при B1 = 1,4 Тл, H1=1200 А/м (рис. 6.15, б); для воздушного зазора напряжённость
Hδ =8·10^5Bδ
Согласно закону полного тока МДС обмотки с числом витков w
F = H1lM + Hδδ = wI
Выбрав значение тока I, определяют число витков w катушки, или, наоборот, выбрав число витков w катушки, находят значение тока I
Обратная задача
Заданы геометрические размеры магнитопровода: lM, δ, S1 =Sδ и кривые намагничивания ферромагнетиков отдельных участков цепи (см. рис. 6.15, а и б), а также МДС F обмотки. Нужно определить магнитный поток Ф в зазоре
Запишем закон полного тока:
H1lM + Hδδ = F = RМЭФ = wI
Откуда искомый магнитный поток
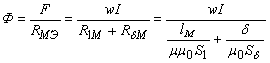
Полученное нелинейное относительно магнитного потока Ф уравнение обычно решают на ЭВМ, выражая зависимость μ(Ф) в аналитической или табличной форме. Приближенное решение можно получить графо-аналитическим методом.
Метод последовательного приближения. В первом приближении примем магнитное сопротивление цепи RМЭ, равное магнитному сопротивлению воздушного зазора, т. е
RМЭ =RdМ = δ / (μ0Sδ) = 8·10^5δ / Sδ
При этом условии возбуждаемый известной МДС F магнитный поток Ф0 в магнитопроводе заведомо больше действительного, т. е
Ф0 = F / RδМ> Ф.
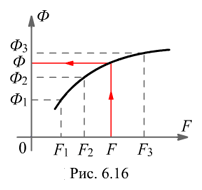
По заданному магнитному потоку Ф и габаритам магнитопровода цепи определяется магнитная индукция
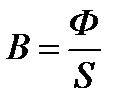
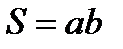где
площадь сечения магнитопровода, которая по всей длине ℓ имеет одинаковое значение
Графический метод.
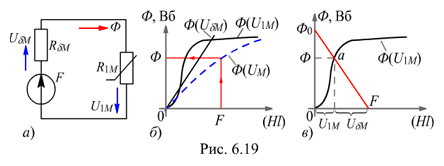
Вычерчиваем схему замещения исследуемой цепи с выделением участка с линейным магнитным сопротивлением RδM и участка с нелинейным сопротивлением R1M (рис. 6.19, а).
МДС схемы замещения
F = ФRδM + ФR1M = UδM + U1M,
Откуда
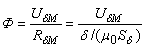- линейная зависимость Ф = f(UδM);
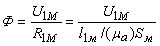- нелинейная зависимость Ф = f(U1M).
Строим на одном рисунке (в выбранном масштабе) три графика (рис . 6.19, б):
● Ф=(f(UδM) для воздушного зазора - прямую линию, угол наклона к оси абсцисс которой пропорционален сопротивлению RδM;
● Ф(U1M) для магнитной цепи без воздушного зазора - кривую, подобную графику B(H) материала, т. к. магнитный поток Ф = BSM пропорционален магнитной индукции В, а магнитное напряжение UM = HlM – напряжённости H,
● Ф = f(UM), откладывая от оси ординат по горизонталям отрезки, равные суммарной длине отрезков кривой Ф(U1M) и прямой Ф(UδM).
Затем из точки F = UM восстанавливаем перпендикуляр до пересечения с пунктирной кривой Ф(UM) и на оси ординат находим искомый магнитный поток Ф.
Расчёт разветвленных магнитных цепей
В разветвлённой магнитной цепи формируется несколько магнитных потоков, которые складываются или вычитаются на некоторых её участках. По аналогии с разветвлённой электрической цепью такая цепь может быть заменена эквивалентной схемой замещения и для неё можно записать уравнения законов Кирхгофа. При этом необх