Привести термодинамические параметры состояния рабочего тела.

Привести термодинамические параметры состояния рабочего тела.

К термодинамическим параметрам состояния системы относят абсолютное давление (р), удельный объем (v) и абсолютную температура(Т).

Термодинамические параметры входят в уравнение состояния вида F(p,v,T) =0 и могут быть непосредственно измерены.

Абсолютное давление.Давление – величина, определяемая отношением силы (ее нормальной составляющей), действующей на поверхность, к площади этой поверхности

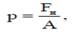
Абсолютная температура

Температура характеризует степень нагретости тела. В настоящее время в практике инженерных расчетов широкое распространение получили две температурные шкалы:

1. Термодинамическая шкала температур, которая имеет одну реперную точку - тройную точку воды (вода находится одновременно в трех фазовых состояниях) при t = 0.01 °С (Т= 273.16 К) и р = 610 Па. Температуру измеряют по шкале Кельвина. К. Начало отсчета

Т = 0 К = - 273.15 °С.

2. Международная практическая шкала температур (МПШТ) имеет две реперные точки: первая точка - точка таяния льда при t₁ = 0°С и р=760 мм рт. ст.; вторая точка - точка кипения воды при t₂ = 100 °С и р = 760 мм рт.ст. МПШТ для измерения температуры использует градусы Цельсия, °С.

Термодинамический параметр — абсолютная температура, выражаемая в Кельвинах. К.

Удельный объем

Удельный объем равен объему единицы массы вещества

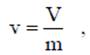
где v - удельный объем, м³/кг; V - объем, м³; m - масса вещества, кг.

Плотность равна массе вещества, содержащегося в единице объема

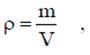
где ρ - плотность вещества, кг/м³ : m - масса вещества, кг; V - объем, м³.

Соотношение между удельным объемом и плотностью вещества

ρv = l.

Удельный вес рассчитывают по формуле, Н/м³

γ = g∙ρ.

2. Дать определения и привести формульные зависимости основных функций состояния.

Основными функциями состояния являются: внутренняя энергия U, Дж; энтальпия Н, Дж; энтропия S, Дж/К.

Внутренняя энергия.

Внутренняя энергия системы включает в себя:

· кинетическую энергию поступательного, вращательного и колебательного движения частиц;

· потенциальную энергию взаимодействия частиц;

· энергию электронных оболочек атомов;

· внутриядерную энергию.

В большинстве теплоэнергетических процессов две последние составляющие остаются неизменными. Под внутренней энергией понимают энергию хаотического движения молекул и атомов, включающую энергию поступательного, вращательного и колебательного движений как молекулярного, так и внутримолекулярного, а также потенциальную энергию сил взаимодействия между молекулами.

Энтальпия.

В термодинамике важную роль играет сумма внутренней энергии системы U и произведения давления системы р на ее объем V, называемая энтальпией и обозначаемая Н:

.

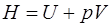Так как входящие в нее величины являются функциями состояния, то и сама энтальпия является функцией состояния. Так же как внутренняя энергия, работа и теплота, она измеряется в джоулях (Дж).

Энтальпия обладает свойством аддитивности. Величина

,

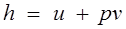называемая удельной энтальпией (h = H/M), представляет собой энтальпию системы, содержащей 1 кг вещества, и измеряется в Дж/кг.

Поскольку энтальпия есть функция состояния, то она может быть представлена в виде функции двух любых параметров состояния:

; ; ,

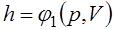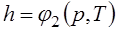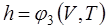а величина dh является полным дифференциалом.

Изменение энтальпии в любом процессе определяется только начальным и конечным состояниями тела и не за­висит от характера процесса.

Энтропия.

Как уже указывалось, величина 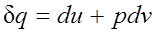не является полным дифференциалом. Действительно, для того чтобы проинтегрировать правую часть этого выражения, нужно знать зависимость р от v, т.е. процесс, который совершает газ.

В математике доказывается, что дифференциальный двучлен всегда можно превратить в полный дифференциал путем умножения (или деления) на интегрирующий множитель (или делитель). Таким интегрирующим делителем для элементарного количества теплоты q является абсолютная температура Т.

Покажем это на примере изменения параметров идеального газа в равновес­ных процессах:

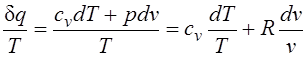, (2.1.3)

где R - газовая постоянная; 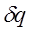- элементарная теплота процесса; c_v - теплоемкость газа при постоянном объеме.

Выражение 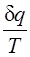при равновесном изменении состояния газа есть полный дифференциал некоторой функции состояния. Она называется энтропией, обозначается для 1 кг газа через s и измеряется в Дж/(кг∙К). Для произвольного количества газа энтропия, обозначаемая через S, равна S=Ms и измеряется в Дж/К.

Таким образом, аналитически энтропия определяется следующим образом:

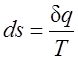. (2.1.4)

Формула (2.1.4) справедлива как для идеальных газов, так и для реальных тел. Подобно любой другой функции состояния энтропия может быть представлена в виде функции любых двух параметров состояния:

; ; .

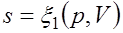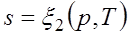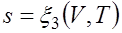Значение энтропии для заданного состояния определяется интегрированием уравнения (2.1.4):

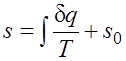
где 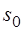— константа интегрирования.

При температурах, близких к абсолютному нулю, все известные вещества находятся в конденсированном состоянии. В. Нернст (1906 г.) экспериментально установил, а М. Планк (1912 г.) окончательно сформулировал следующий принцип: при температуре , стремящейся к абсолютному нулю, энтропия вещества, находящегося в конденсированном состоянии с упорядоченной кристаллической структурой, стремится к нулю, т.е. s₀ = 0 при Т = 0 К. Этот закон называют третьим законом термодинамики или тепловой теоремой Нернста.

Привести термодинамические параметры состояния рабочего тела.

К термодинамическим параметрам состояния системы относят абсолютное давление (р), удельный объем (v) и абсолютную температура(Т).

Термодинамические параметры входят в уравнение состояния вида F(p,v,T) =0 и могут быть непосредственно измерены.

Абсолютное давление.Давление – величина, определяемая отношением силы (ее нормальной составляющей), действующей на поверхность, к площади этой поверхности

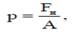
Абсолютная температура

Температура характеризует степень нагретости тела. В настоящее время в практике инженерных расчетов широкое распространение получили две температурные шкалы:

1. Термодинамическая шкала температур, которая имеет одну реперную точку - тройную точку воды (вода находится одновременно в трех фазовых состояниях) при t = 0.01 °С (Т= 273.16 К) и р = 610 Па. Температуру измеряют по шкале Кельвина. К. Начало отсчета

Т = 0 К = - 273.15 °С.

2. Международная практическая шкала температур (МПШТ) имеет две реперные точки: первая точка - точка таяния льда при t₁ = 0°С и р=760 мм рт. ст.; вторая точка - точка кипения воды при t₂ = 100 °С и р = 760 мм рт.ст. МПШТ для измерения температуры использует градусы Цельсия, °С.

Термодинамический параметр — абсолютная температура, выражаемая в Кельвинах. К.

Удельный объем

Удельный объем равен объему единицы массы вещества

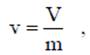
где v - удельный объем, м³/кг; V - объем, м³; m - масса вещества, кг.

Плотность равна массе вещества, содержащегося в единице объема

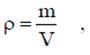
где ρ - плотность вещества, кг/м³ : m - масса вещества, кг; V - объем, м³.

Соотношение между удельным объемом и плотностью вещества

ρv = l.

Удельный вес рассчитывают по формуле, Н/м³

γ = g∙ρ.

2. Дать определения и привести формульные зависимости основных функций состояния.

Основными функциями состояния являются: внутренняя энергия U, Дж; энтальпия Н, Дж; энтропия S, Дж/К.

Внутренняя энергия.

Внутренняя энергия системы включает в себя:

· кинетическую энергию поступательного, вращательного и колебательного движения частиц;

· потенциальную энергию взаимодействия частиц;

· энергию электронных оболочек атомов;

· внутриядерную энергию.

В большинстве теплоэнергетических процессов две последние составляющие остаются неизменными. Под внутренней энергией понимают энергию хаотического движения молекул и атомов, включающую энергию поступательного, вращательного и колебательного движений как молекулярного, так и внутримолекулярного, а также потенциальную энергию сил взаимодействия между молекулами.

Энтальпия.

В термодинамике важную роль играет сумма внутренней энергии системы U и произведения давления системы р на ее объем V, называемая энтальпией и обозначаемая Н:

.

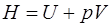Так как входящие в нее величины являются функциями состояния, то и сама энтальпия является функцией состояния. Так же как внутренняя энергия, работа и теплота, она измеряется в джоулях (Дж).

Энтальпия обладает свойством аддитивности. Величина

,

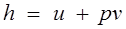называемая удельной энтальпией (h = H/M), представляет собой энтальпию системы, содержащей 1 кг вещества, и измеряется в Дж/кг.

Поскольку энтальпия есть функция состояния, то она может быть представлена в виде функции двух любых параметров состояния:

; ; ,

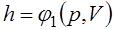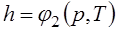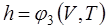а величина dh является полным дифференциалом.

Изменение энтальпии в любом процессе определяется только начальным и конечным состояниями тела и не за­висит от характера процесса.

Энтропия.

Как уже указывалось, величина 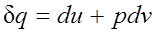не является полным дифференциалом. Действительно, для того чтобы проинтегрировать правую часть этого выражения, нужно знать зависимость р от v, т.е. процесс, который совершает газ.

В математике доказывается, что дифференциальный двучлен всегда можно превратить в полный дифференциал путем умножения (или деления) на интегрирующий множитель (или делитель). Таким интегрирующим делителем для элементарного количества теплоты q является абсолютная температура Т.

Покажем это на примере изменения параметров идеального газа в равновес­ных процессах:

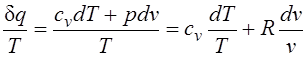, (2.1.3)

где R - газовая постоянная; 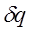- элементарная теплота процесса; c_v - теплоемкость газа при постоянном объеме.

Выражение 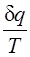при равновесном изменении состояния газа есть полный дифференциал некоторой функции состояния. Она называется энтропией, обозначается для 1 кг газа через s и измеряется в Дж/(кг∙К). Для произвольного количества газа энтропия, обозначаемая через S, равна S=Ms и измеряется в Дж/К.

Таким образом, аналитически энтропия определяется следующим образом:

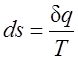. (2.1.4)

Формула (2.1.4) справедлива как для идеальных газов, так и для реальных тел. Подобно любой другой функции состояния энтропия может быть представлена в виде функции любых двух параметров состояния:

; ; .

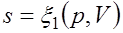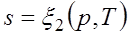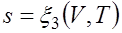Значение энтропии для заданного состояния определяется интегрированием уравнения (2.1.4):

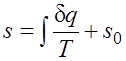
где 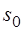— константа интегрирования.

При температурах, близких к абсолютному нулю, все известные вещества находятся в конденсированном состоянии. В. Нернст (1906 г.) экспериментально установил, а М. Планк (1912 г.) окончательно сформулировал следующий принцип: при температуре , стремящейся к абсолютному нулю, энтропия вещества, находящегося в конденсированном состоянии с упорядоченной кристаллической структурой, стремится к нулю, т.е. s₀ = 0 при Т = 0 К. Этот закон называют третьим законом термодинамики или тепловой теоремой Нернста.