Частные случаи политропных процессов
изобарный Р=const
| n=0 | 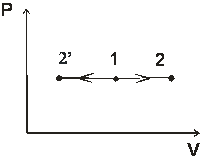 | 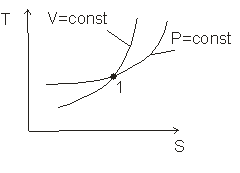 |
| Уравнение процесса | 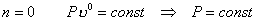 , или , или 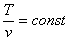 | |
| Теплоемкость | 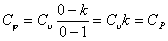 | |
| Изменение энтропии | 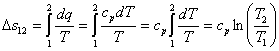 | |
| Работа расширения | 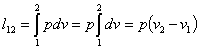 | |
| Количество теплоты | 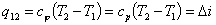 | |
| Изменение внутренней энергии | 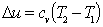 | |
| Изменение энтальпии | 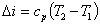 | |
| I закон термодинамики | 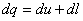 |
изотермический T=const
| n=1 | 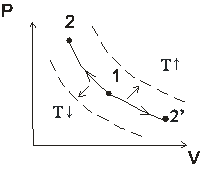 | 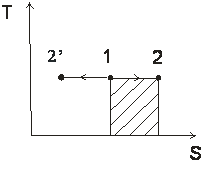 |
| Уравнение процесса | 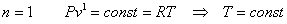 | |
| Теплоемкость | 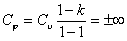 | |
| Изменение энтропии | ds= 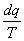 ; q=l (согласно I закона ТД) ; q=l (согласно I закона ТД) 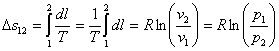 | |
| Работа расширения | 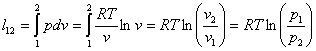 | |
| Количество теплоты | 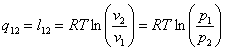 | |
| Изменение внутренней энергии | 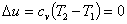 | |
| Изменение энтальпии | 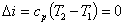 | |
| I закон термодинамики | 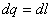 Вся подведенная теплота идет на совершение работы. Вся подведенная теплота идет на совершение работы. |
адиабатный dq=0
n=k 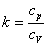 | 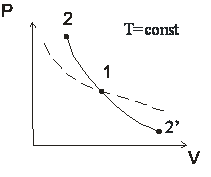 | 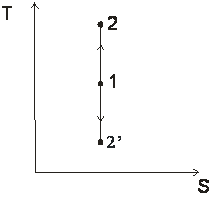 |
| Уравнение процесса | 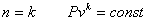 ( уравнение Пуассона). ( уравнение Пуассона). | |
| Теплоемкость | 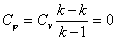 | |
| Изменение энтропии | ds= 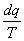 = 0, т. е. s = const (изоэнтропийный процесс) = 0, т. е. s = const (изоэнтропийный процесс) | |
| Работа расширения | 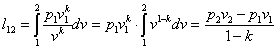 | |
| Количество теплоты | 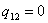 | |
| Изменение внутренней энергии | 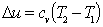 | |
| Изменение энтальпии | 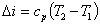 | |
| I закон термодинамики | 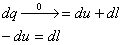 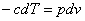 Работа совершается за счет внутренней энергии Работа совершается за счет внутренней энергии |
изохронный V=const
| n=±∞ | 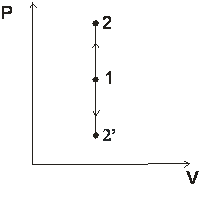 |  |
| Уравнение процесса | 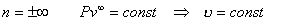 | |
| Теплоемкость | 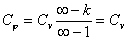 | |
| Изменение энтропии | 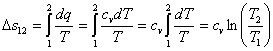 | |
| Работа расширения | 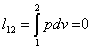 | |
| Количество теплоты | 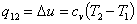 | |
| Изменение внутренней энергии | 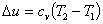 | |
| Изменение энтальпии | 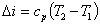 | |
| I закон термодинамики | 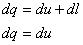 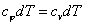 Вся подведенная теплота идет на изменение внутренней энергии Вся подведенная теплота идет на изменение внутренней энергии |
Обобщенная диаграмма политропных процессов.
Для анализа политропных процессов удобно пользоваться обобщенной диаграммой. На ней изображаются все изопроцессы и выделяются области, в пределах которых знаки сл агаемых I закона одинаковы.
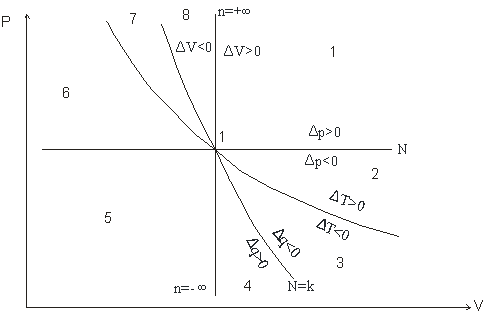 | ||
| Рабочая диаграмма | ||
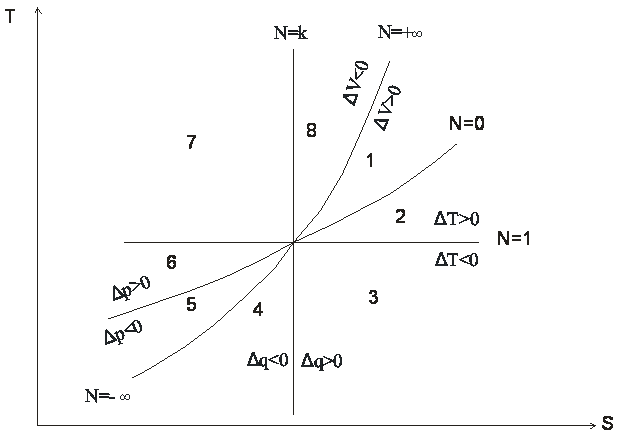 | ||
| Тепловая диаграмма |
Диаграмма позволяет проанализировать любой политропный процесс и определить условия, при которых этот процесс может быть реализован, то есть, как распределяется теплота между внутренней энергией и работой, что будет с температурой системы и т.д.
1. Любой процесс, лежащий выше изобары проведённой через точку 1 сопровождается ростом давления.
2. Любой процесс, лежащий выше изотермы сопровождается ростом температуры, внутренней энергии и энтальпии.
3. Любой процесс, лежащий правее адиабаты сопровождается ростом энтрапии и подводом теплоты.
4. Любой процесс, лежащий правее изохоры идёт с ростом объёма и работа в процессе положительна.
14. Понятие прямого и обратного термодинамического цикла
Прямые и обратные циклы
Общетехнические дисциплины / Теплотехника / 9.1. Прямые и обратные циклы
Состояние рабочего тела определяется его параметрами. Под воздействием внешних сил рабочее тело изменяет свое состояние, связанное с изменением его параметров, т.е, протекает термодинамический процесс.
Последовательный ряд термодинамических процессов, в которых рабочее тело претерпевает изменение и в результате возвращается в первоначальное состояние, называется круговым процессом или циклом.
Циклы подразделяются на прямые и обратные. Прямыми называют циклы, в которых теплота преобразуется в работу, обратными – в которых теплота передается от более холодного тела к более нагретому.
Прямые циклы изображаются в диаграммах линиями, идущими по часовой стрелке (по таким циклам работают тепловые двигатели), обратные циклы – линиями, идущими против часовой стрелки (по таким циклам работают холодильные машины и тепловые насосы).
Прямой цикл
Рассмотрим систему, состоящую из двух источников теплоты и рабочего тела. При изучении идеальных циклов процесс подвода теплоты рассматривается без изменения химического состава рабочего тела. В большинстве реально существующих двигателей теплота подводится в процессе сгорания топлива. Процесс отвода теплоты рассматривается как передача теплоты к источнику с низкой температурой. В реальных двигателях теплота может отводиться вместе с выпуском отработавшего рабочего тела (пара или газа) в атмосферу. В pv-диаграмме прямой цикл изображается так, как показано на рис. 9.1.
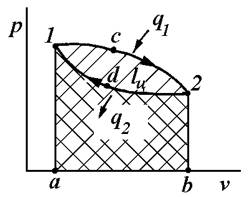
Рис. 9.1. Прямой цикл
Если от более нагретого источника теплоты к рабочему телу подвести теплоту q1 , то состояние рабочего тела меняется, происходит расширение по линии 1–с–2. Полезную работу, совершенную в процессе расширения 1–с–2 можно определить площадью 1–с–2–b–а–1.
В процессе 2–d–1 рабочее тело взаимодействует с источником низких температур. При этом происходит отвод теплоты q2 от рабочего тела и его сжатие. В процессе сжатия затрачивается работа, величина которой равна площади a–1–d–2–b–a. Из диаграммы видно, что работа расширения больше работы сжатия. Полезная работа равна разности работ расширения и сжатия:
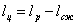 .
.
В результате совершения такого цикла получается полезная работа, которую затем можно использовать для различных целей.
В соответствие с первым законом термодинамики 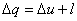 для рассматриваемого кругового цикла
для рассматриваемого кругового цикла 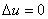 , и поэтому
, и поэтому 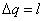 или
или
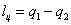 .
.
Для оценки степени совершенства прямых циклов используется термический коэффициент полезного действия ( 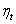 ), под которым понимается отношение работы, полученной в цикле, к затраченной теплоте:
), под которым понимается отношение работы, полученной в цикле, к затраченной теплоте:
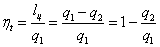 .
.
Обратный цикл
Пусть имеется два источника теплоты и рабочее тело, над которым совершается работа.
Рабочее тело переносит теплоту q2 от источника с низкой температурой к источнику с более высокой температурой. На совершение такого несамопроизвольного процесса затрачивается работа lц.
Процесс расширения рабочего тела осуществляется с подводом теплоты q2 по линии 1–d–2 (рис. 9.2). В этом процессе полезная работа равна площади 1–d–2–b–a–1. В процессе сжатия 2–с–1 рабочее тело взаимодействует с источником с более высокой температурой, передавая ему теплоту q1. В процессе сжатия затрачивается работа, равная площади 2–c–1–a–b–2.
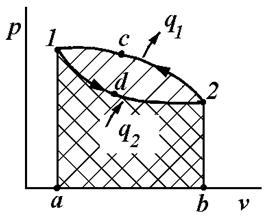
Рис. 9.2. Обратный цикл
Из диаграммы видно, что работа сжатия больше работы расширения. Работа цикла получается отрицательной. В результате совершения обратного цикла теплота отбирается от источника с низкой температурой и передается к источнику с высокой температурой.
Для оценки работы холодильных машин применяется холодильный коэффициент, равный отношению полезного количества теплоты (q2), отнятого от холодного источника, к затраченной работе:
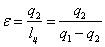 .
.
В холодильной машине количество теплоты q1 выбрасывается в окружающую среду, т.е. в источник неограниченных размеров.
Машины, предназначенные для дальнейшего использования теплоты q1 и передачи ее в источник ограниченных размеров, называют тепловыми насосами. Эффективность работы тепловых насосов оценивается отопительным коэффициентом, представляющим собой отношение количества теплоты (q1), переданного потребителю, к затраченной работе:
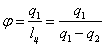 .
.
15. Прямой цикл карно
В термодинамике цикл Карно́ или процесс Карно — это обратимый круговой процесс, состоящий из двух адиабатических и двух изотермических процессов[1]. В процессе Карно термодинамическая система выполняет механическую работу и обменивается теплотой с двумя тепловыми резервуарами, имеющими постоянные, но различающиеся температуры. Резервуар с более высокой температурой называется нагревателем, а с более низкой температурой — холодильником[2].
Цикл Карно назван в честь французского учёного и инженера Сади Карно, который впервые его описал в своём сочинении «О движущей силе огня и о машинах, способных развивать эту силу» в 1824 году[3][4].
Поскольку обратимые процессы могут осуществляться лишь с бесконечно малой скоростью, мощность тепловой машины в цикле Карно равна нулю. Мощность реальных тепловых машин не может быть равна нулю, поэтому реальные процессы могут приближаться к идеальному обратимому процессу Карно только с большей или меньшей степенью точности. В цикле Карно тепловая машина преобразует теплоту в работу с максимально возможным коэффициентом полезного действия из всех тепловых машин, у которых максимальная и минимальная температуры в рабочем цикле совпадают соответственно с температурами нагревателя и холодильника в цикле Карно[5].
Описание цикла Карно[править | править вики-текст]
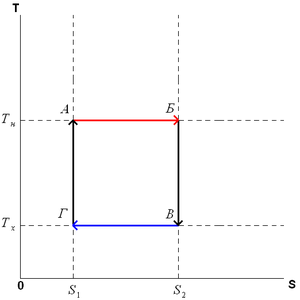
Рис. 1. Цикл Карно в координатах T—S
Пусть тепловая машина состоит из нагревателя с температурой {\displaystyle T_{H}}, холодильника с температурой {\displaystyle T_{X}} и рабочего тела.
Цикл Карно состоит из четырёх обратимых стадий, две из которых осуществляются при постоянной температуре (изотермически), а две — при постоянной энтропии (адиабатически). Поэтому цикл Карно удобно представить в координатах T (температура) и S (энтропия).
1. Изотермическое расширение (на рис. 1 — процесс A→Б). В начале процесса рабочее тело имеет температуру {\displaystyle T_{H}}, то есть температуру нагревателя. Затем тело приводится в контакт с нагревателем, который изотермически (при постоянной температуре) передаёт ему количество теплоты {\displaystyle Q_{H}}. При этом объём рабочего тела увеличивается, оно совершает механическую работу, а его энтропия возрастает.
2. Адиабатическое расширение (на рис. 1 — процесс Б→В). Рабочее тело отсоединяется от нагревателя и продолжает расширяться без теплообмена с окружающей средой. При этом температура тела уменьшается до температуры холодильника {\displaystyle T_{X}}, тело совершает механическую работу, а энтропия остаётся постоянной.
3. Изотермическое сжатие (на рис. 1 — процесс В→Г). Рабочее тело, имеющее температуру {\displaystyle T_{X}}, приводится в контакт с холодильником и начинает изотермически сжиматься под действием внешней силы, отдавая холодильнику количество теплоты {\displaystyle Q_{X}}. Над телом совершается работа, его энтропия уменьшается.
4. Адиабатическое сжатие (на рис. 1 — процесс Г→А). Рабочее тело отсоединяется от холодильника и сжимается под действием внешней силы без теплообмена с окружающей средой. При этом его температура увеличивается до температуры нагревателя, над телом совершается работа, его энтропия остаётся постоянной.
Рис. 2. Цикл Карно на термодинамической поверхности идеального газа
Обратный цикл Карно[править | править вики-текст]
В термодинамике холодильных установок и тепловых насосов рассматривают обратный цикл Карно, состоящий из следующих стадий[6][7]: адиабатического сжатия за счёт совершения работы (на рис. 1 — процесс В→Б); изотермического сжатия с передачей теплоты более нагретому тепловому резервуару (на рис. 1 — процесс Б→А); адиабатического расширения (на рис. 1 — процесс А→Г); изотермического расширения с отводом теплоты от более холодного теплового резервуара (на рис. 1 — процесс Г→В).
КПД тепловой машины Карно[править | править вики-текст]
Количество теплоты, полученное рабочим телом от нагревателя при изотермическом расширении, равно
{\displaystyle Q_{H}=\int TdS=T_{H}(S_{2}-S_{1})=T_{H}\Delta S}.
Аналогично, при изотермическом сжатии рабочее тело отдаёт холодильнику
{\displaystyle Q_{X}=T_{X}(S_{2}-S_{1})=T_{X}\Delta S}.
Отсюда коэффициент полезного действия тепловой машины Карно равен
{\displaystyle \eta ={\frac {Q_{H}-Q_{X}}{Q_{H}}}={\frac {T_{H}-T_{X}}{T_{H}}}}.
Первая и вторая теоремы Карно[править | править вики-текст]
Основная статья: Теорема Карно (термодинамика)
Из последнего выражения следует, что КПД тепловой машины, работающей по циклу Карно, зависит только от температур нагревателя и холодильника, но не зависит ни от устройства машины, ни от вида или свойств её рабочего тела. Этот результат составляет содержание первой теоремы Карно[8]. Кроме того, из него следует, что КПД может составлять 100 % только в том случае, если температура холодильника равна абсолютному нулю. Это невозможно, но не из-за недостижимости абсолютного нуля (этот вопрос решается только третьим началом термодинамики, учитывать которое здесь нет необходимости), а из-за того, что такой цикл или нельзя замкнуть, или он вырождается в совокупность двух совпадающих адиабат и изотерм.
Поэтому максимальный КПД любой тепловой машины не может превосходить КПД тепловой машины Карно, работающей при тех же температурах нагревателя и холодильника. Это утверждение называется второй теоремой Карно[5][9]. Оно даёт верхний предел КПД любой тепловой машины и позволяет оценить отклонение реального КПД от максимального, то есть потери энергии вследствие неидеальности тепловых процессов.
Связь между обратимостью цикла и КПД[править | править вики-текст]
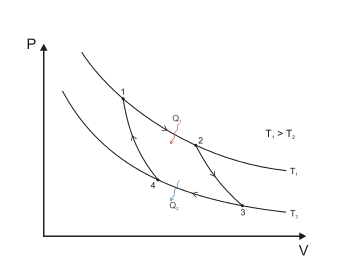
Рис. 3. Цикл Карно в координатах P и V
Для того чтобы цикл был обратимым, в нём должна быть исключена передача теплоты при наличии разности температур, иначе нарушается условие адиабатичности процесса. Поэтому передача теплоты должна осуществляться либо в изотермическом процессе (как в цикле Карно), либо в эквидистантном процессе (обобщённый цикл Карно или, для примера, его частный случай Цикл Брайтона). Для того чтобы менять температуру рабочего тела от температуры нагревателя до температуры холодильника и обратно, необходимо использовать либо адиабатические процессы (они идут без теплообмена и, значит, не влияют на энтропию), либо циклы с регенерацией тепла при которых нет передачи тепла при разности температур. Мы приходим к выводу, что любой обратимый цикл может быть сведён к циклу Карно.
Примером обратимого цикла, не являющегося циклом Карно, но интегрально совпадающим с ним, является идеальный цикл Стирлинга: в двигателе Стирлинга добавлен регенератор, обеспечивающий полное приближение цикла к циклу Карно с достижением обратимости и тех же величин КПД[10]. Возможны и другие идеальные циклы, в которых коэффициент полезного действия определяется по той же формуле, что и для циклов Карно и Стирлинга[10], например цикл Эрикссона, состоящий двух изобар и двух изотерм[11].
Если же в цикле возникает передача теплоты при наличии разности температур, а таковыми являются все технические реализации термодинамических циклов, то цикл утрачивает свойство обратимости. Иначе говоря, посредством отведённой в цикле механической работы становится невозможным получить исходную теплоту. КПД такого цикла будет всегда меньше, чем КПД цикла Карно.
16. Циклы поршневых ДВС
Циклы поршневых двигателей внутреннего сгорания подразделяют на три группы:
- с подводом теплоты при постоянном объеме (карбюраторные ДВС);
- с подводом теплоты при постоянном давлении (компрессорные дизели);
- со смешанным подводом теплоты при постоянном объеме (безкомпрессорные дизели);
Основными характеристиками или параметрами любого цикла теплового двигателя являются следующие безрамерные величины:
степень сжатия (отношение удельных объемов рабочего тела в начале и конце сжатия)
e = n1 / n2 , (7.5)
степень повышения давления (отношение давлений в конце и в начале изохорного процесса подвода теплоты)
l = Р3 / Р2 , (7.6)
степень предварительного расширения или степень изобарного расширения (отношение удельных объемов в конце и в начале изохорного процесса подвода теплоты)
r = n3 / n2 . (7.7)
1). Рассмотрим цикл ДВС с подводом теплоты при постоянном объеме на примере четырехтактного двигателя.
Диаграмма реального двигателя представлена на рис.7.3.
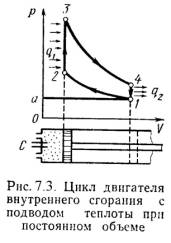
а-1 (1 такт) – в цилиндр через всасывающий клапан поступает смесь воздуха и паров горючего (нетермодинамичемкий процесс);
1-2 (2 такт) – адиабатное сжатие (повышается температура);
2-3 – сгорание горючей смеси, давление быстро возрастает при постоянном объеме (подвод теплоты q1);
3-4 (3 такт) – адиабатное расширение (рабочий процесс, совершается полезная работа);
4-а – открывается выхлопной клапан и отработанные газы покидают цилиндр давление цилиндра падает (отводится тепло q2).
1-а (4 такт) – выталкивание оставшихся в цилиндре газов.
Затем процесс повторяется.
Описанный процесс является необратимым (наличие трения, химической реакции в рабочем теле, конечные скорости поршня, теплообмен при конечной разности температур и т.п.).
Для анализа теории тепловых машин термодинамика рассматривает идеальные циклы обратимые циклы. Диаграмма идеального процесса двигателя внутреннего сгорания показана на рис.7.4.
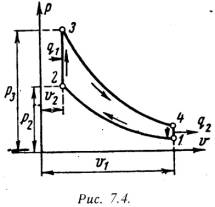
Из этой диаграммы выводится формула для термического к.п.д. цикла с подводом теплоты при постоянном объеме, который имеет следующий вид:
ht = 1 – 1/eg , (7.8)
где: e –степень сжатия (основной показатель работы двигателя, чем выше е, тем выше экономичность ДВС);
g – показатель адиабаты.
2). Идеальный цикл ДВС со смещанным подводом теплоты при постоянном объеме (безкомпрессорные дизели). Диаграмма цикла показана на рис.7.5.

1-2 - чистый воздух с температурой Т1 сжимается до температуры Т2, которая больше температуры воспламенениятоплива. В этот момент в цилиндр через форсунки под давлением впрыскивается топливо.
2-3 – горючая смесь самовоспламеняется и к рабочему телу подводится тепло q1/, давление повышается до Р3.
3-4 – поршень перемешается обратно, поступление и сгорание топлива продолжается при постоянном давлении и подводится тепло q1//.
4-5 – поршень продолжает перемещаться в нижнюю мертвую точку, давление падает (адиабатное расширение);
5-1 – процесс отвода теплоты q2 при постоянном объеме (через выпускной клапан покидают отработанные газы).
Термический к.п.д. цикла определяется по формуле:
ht = l – (l·rg – 1) / eg-1·[(l - 1) + g·l·(r – 1)] . (7.9)
Цикл двигателей с подводом теплоты при постоянном давлении широкое применение не нашли, так как у этих циклов очень большой коэффициент сжатия.
17. Циклы газоторбиной установки
