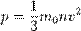Векторное изображение гармонических колебаний.

Гармонические колебания изображают графически оборотным вектором амплитуды. Проекция этого вектора на ось 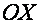равняется смещению 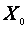в начальный момент времени :

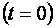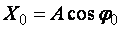. (11.21)

Будем вращать вектор 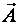вокруг точки 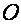против хода часовой стрелки с угловой скоростью 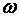, которая равняется циклический частоте колебаний . За промежуток времени 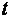вектор 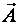осуществит поворот на угол 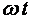, и его проекция на ось 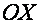будет:

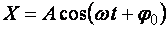. (11.22)

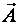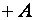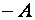В процессе вращения вектора его проекция на опорную ось будет изменяться от до по гармоническому закону.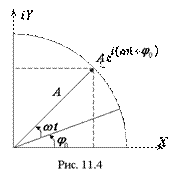

Если колебание описывать по закону косинуса

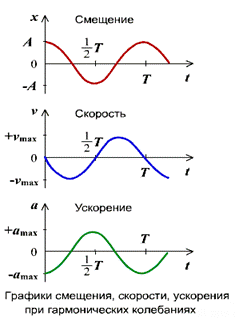
Если колебание описывать по закону синуса

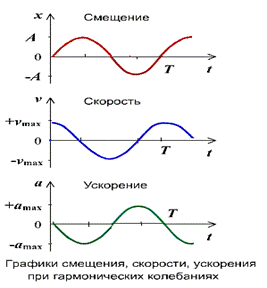
Графики зависимостей кинетической и потенциальной энергий

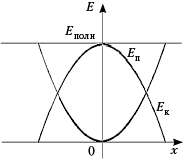
График Е_п(х) объясняется учащимися легко, исходя из формулы Е_п = kx²/2. Обращённые вверх ветви параболы соответствуют положительному коэффициенту при x², симметричность графика относительно вертикальной оси указывает на одинаковое значение потенциальной энергии в случаях растяжения и сжатия при равных изменениях длины пружины.

Действительно, кинетическую энергию можно выразить как разность между значениями полной энергии, которая в случае незатухающих колебаний является величиной постоянной, и потенциальной энергии: Е_к = Е_полн – Е_п = const – kx²/2.

Энергия гармонических колебаний

Кинетическая энергия тела совершающего гармонические колебания равна :

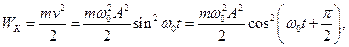
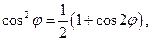
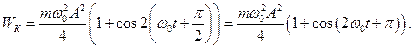
Потенциальная энергия равна

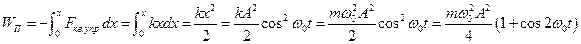
Полная энергия равна

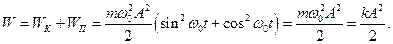
Квазиупругая сила является консервативной, поэтому полная энергия гармонического колебания остается постоянной. В процессе колебаний происходит превращение кинетической энергии в потенциальную и обратно. Колебания W_К и W_П происходят с частотой 2ω₀, т.е. в два раза превышающей частоту гармонических колебаний.

17)

Вынужденные механические колебания.Свободные колебания реальной колебательной системы являются затухающими. Чтобы колебания были незатухающими, необходимо компенсировать потери энергии, обусловленные силами сопротивления. Это можно сделать, воздействуя на систему (рис.27.3) внешней силой, изменяющейся по гармоническому закону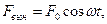

где 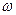- частота вынуждающей силы.

Уравнение движения запишется с учетом всех сил ( 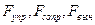) запишется в виде

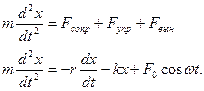
Поделив обе части на m и перенося первые два члена из правой части в левую, получим

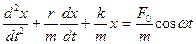
Обозначив, как и в п.6 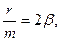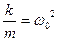, получим дифференциальное уравнение вынужденных колебаний 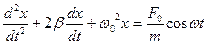(13)

Уравнение является неоднородным. Общее решение неоднородного уравнения равно сумме общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения

.

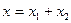Общее решение однородного уравнения (правая часть (13) равна нулю) нам уже известно

.

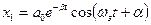Роль х1 уменьшается и по прошествии некоторого времени им можно пренебречь и остаётся только частные решения неоднородного уравнения (без вывода) 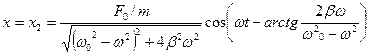(14)

Функция (14) описывает установившиеся вынужденные гармонические колебания с частотой, равной частоте вынужденной силы.

Амплитуда вынужденных колебаний пропорциональна амплитуде вынуждающей силы. Для данной колебательной системы (определенных 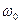и 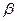) амплитуда зависит от частоты вынуждающей силы. Вынужденные колебания отстают по фазе от вынуждающей силы, причем величина отставания также зависит от частоты вынуждающей силы.

Механический резонанс. Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы приводит к тому, что при некоторой определенной для данной системы частоте амплитуда колебаний достигает максимального значения. Это явление называется резонансом, а соответствующая частота – резонансной частотой.

Чтобы найти резонансную частоту 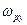, нужно найти максимум амплитуды функции (14), т.е. максимум функции 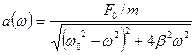(15)

Или, что-то же самое, найти минимум выражения, стоящего под корнем в знаменателе (15). Продифференцировав выражение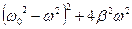

по 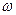и приравняв к нулю, получим

.

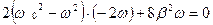Проведя дальнейшие простые преобразования, получим

,

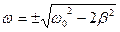а т.к. частота по своему смыслу не может быть отрицательной, то выбираем решение со знаком «+». Итак, резонансная частота

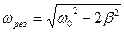(16)

Резонансная кривая - зависимость амплитуды установившихся колебаний маятника от частоты вынуждающей силы.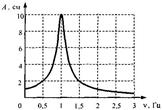

18)

Механические волны — это процесс распространения в пространстве колебаний частиц упругой среды (твёрдой, жидкой или газообразной).

Наличие у среды упругих свойств является необходимым условием распространения волн: деформация, возникающая в каком-либо месте, благодаря взаимодействию соседних частиц последовательно передаётся от одной точки среды к другой. Различным типам деформаций будут соответствовать разные типы волн.

Скоростью распространения волны называется отношение длины волны к периоду колебаний частиц среды:

v =λ/T

Частотой волны называется частота колебаний частиц:

ν =1/T

Отсюда получаем связь скорости волны, длины волны и частоты:

v = λν

Продольные и поперечные волны

Волна называется продольной, если частицы среды колеблются параллельно направлению распространения волны. Продольная волна состоит из чередующихся деформаций растяжения и сжатия.

Волна называется поперечной, если частицы среды колеблются перпендикулярно направлению распространения волны. Поперечная волна вызывается деформациями сдвига одного слоя среды относительно другого.

Продольные волны могут распространяться в твёрдых телах, жидкостях и газах: во всех этих средах возникает упругая реакция на сжатие, в результате которой появятся бегущие друг за другом сжатия и разрежения среды.

Однако жидкости и газы, в отличие от твёрдых тел, не обладают упругостью по отношению к сдвигу слоёв. Поэтому поперечные волны могут распространяться в твёрдых телах, но не внутри жидкостей и газов.

Уравнение плоской гармонической воны, распространяющейся вдоль оси x:

S=Acos((ωt-x/v)+φ0)

Закон Гука:

Сила упругости, возникающая при деформации тела, пропорциональна удлинению этого тела.

F=-kx

u= (Eε^2)/2 - плотность энергии упругой деформации при растяжении (или сжатии)

W=m/2((〖∂ε/∂t)〗^2+v^2 (〖∂ε/∂x)〗^2)-энергия упругой волны

Плотность потока энергии - вектор, физическая величина j, численно равная потоку энергии через единичную площадку, помещенную в данной точке перпендикулярно направлению переноса энергии.

Направление j (вектор!) совпадает с направлением переноса энергии

j=∆E/∆t∆S=∆ϕ/∆S

19)

Специальная теория относительности (СТО) представляет собой современную физическую теорию пространства и времени. СТО часто называют релятивистской теорией, а специфические явления, описываемые этой теорией, – релятивистскими эффектами. Эти эффекты наиболее отчетливо проявляются при скоростях движения тел, близких к скорости света в вакууме c ≈ 3·10⁸ м/с. Специальная теория относительности была создана А. Эйнштейном (1905 г.).

Классическая механика Ньютона прекрасно описывает движение макротел, движущихся с малыми скоростями (υ << c). В основе классической механики лежит механический принцип относительности: законы динамики одинаковы во всех инерциальных системах отсчета. Этот принцип означает, что законы динамики инвариантны (т. е. неизменны) относительно преобразований Галилея, которые позволяют вычислить координаты движущегося тела в одной инерциальной системе (K), если заданы координаты этого тела в другой инерциальной системе (K').

В основе специальной теории относительности лежат два принципа или постулата, сформулированные Эйнштейном в 1905 г.

1)Принцип относительности: все законы природы инвариантны по отношению к переходу от одной инерциальной системы отсчета к другой. Это означает, что во всех инерциальных системах физические законы (не только механические) имеют одинаковую форму. Таким образом, принцип относительности классической механики обобщается на все процессы природы, в том числе и на электромагнитные. Этот обобщенный принцип называют принципом относительности Эйнштейна.

2)Принцип постоянства скорости света: скорость света в вакууме не зависит от скорости движения источника света или наблюдателя и одинакова во всех инерциальных системах отсчета. Скорость света в СТО занимает особое положение. Это предельная скорость передачи взаимодействий и сигналов из одной точки пространства в другую.

Эти принципы следует рассматривать как обобщение всей совокупности опытных фактов.

Преобразования Лоренца

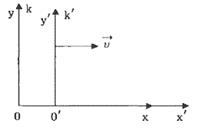
Пусть нам даны две системы отсчета k и k`. В момент t = 0 обе эти системы координат совпадают. Пусть система k` (назовем ее подвижной) движется так, что ось х` скользит по оси х, ось у` параллельна оси у, скорость v - скорость движения этой системы координат (рис. 109).

Точка М имеет координаты в системе k - х, у, z, a в системе k` - х`, у`, z`.

Преобразования Галилея в классической механике имеют вид:

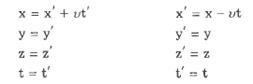
Преобразования координат, удовлетворяющие постулатам специальной теории относительности, называются преобразованиями Лоренца.

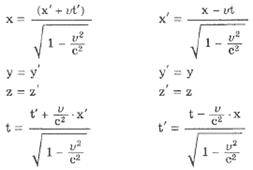
Следствия из преобразований Лоренца

1)Длина движущегося стержня.

Предположим, что стержень расположен вдоль оси х` в системе k` и движется вместе с системой k` со скоростью v.

Разность между координатами конца и начала отрезка в системе отсчета, в которой он неподвижен, называется собственной длиной отрезка. В нашем случае l₀ = х₂` - х<sub>1</sub>`, где х₂` - координата конца отрезка в системе k` и х/ - координата начала. Относительно системы k стержень движется. Длиной движущегося стержня принимают разность между координатами конца и начала стержня в один и тот же момент времени по часам системы k.

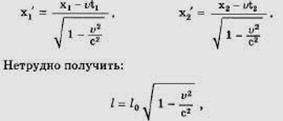
где l - длина движущегося стержня, l₀ - собственная длина стержня. Длина движущегося стержня меньше собственной длины.

2)Темп хода движущихся часов.

Пусть в точке х₀` движущейся системы координат k` происходит последовательно два события в моменты t₁ и t₂. В неподвижной системе координат k эти события происходят в разных точках в моменты t₁ и t₂. Интервал времени между этими событиями в движущейся системе координат равен дельта t` = t<sub>2</sub>` - t₁`, а в покоящейся дельта t = t₂ - t₁.

На основании преобразования Лоренца получим:

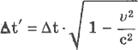
Интервал времени дельта t` между событиями, измеренный движущимися часами, меньше, чем интервал времени дельта t между теми же событиями, измеренный покоящимися часами. Это означает, что темп хода движущихся часов замедлен относительно неподвижных.

Время, которое измеряется по часам, связанным с движущейся точкой, называется собственным временем этой точки.

3)Относительность одновременности.

Из преобразований Лоренца следует, что если в системе k в точке с координатами x₁ и х₂ происходили два события одновременно (t₁ = t₂ = t₀), то в системе k` интервал

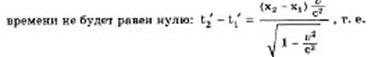
понятие одновременности - понятие относительное. События, одновременные в одной системе координат, оказались неодновременными в другой.

4)Относительность одновременности и причинность.

Из относительности одновременности следует, что последовательность одних и тех же событий в различных системах координат различна.

Не может ли случиться так, что в одной системе координат причина предшествует следствию, а в другой, наоборот, следствие предшествует причине?

Чтобы причинно-следственная связь между событиями имела объективный характер и не зависела от системы координат, в которой она рассматривается, необходимо, чтобы никакие материальные воздействия, осуществляющие физическую связь событий, происходящих в различных точках, не могли передаваться со скоростью, большей скорости света.

Таким образом, передача физического влияния из одной точки в другую не может происходить со скоростью, большей скорости света. При этом условии причинная связь событий носит абсолютный характер: не существует системы координат, в которой причина и следствие меняются местами.

Сложение скоростей

Непосредственным следствием преобразований Лоренца является релятивистское правило сложения скоростей. Если некоторый объект имеет компоненты скорости 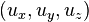относительно системы S и 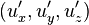— относительно S', то между ними существует следующая связь:

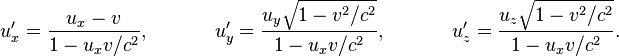
В этих соотношениях относительная скорость движения систем отсчёта v направлена вдоль оси x. Релятивистское сложение скоростей, как и преобразования Лоренца, при малых скоростях ( 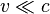) переходит в классический закон сложения скоростей.

Если объект движется со скоростью света 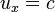вдоль оси x относительно системы S, то такая же скорость у него будет и относительно S': 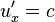. Это означает, что скорость является инвариантной (одинаковой) во всех ИСО.

Энергия и импульс

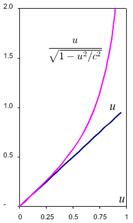Релятивистский и классический импульс, m=1

Если частица с массой (покоя) 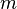движется со скоростью 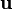, то её энергия и импульс имеют следующую зависимость от скорости:

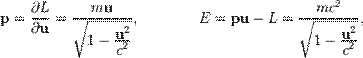
Эти соотношения обобщают классические выражения для энергии и импульса, получающиеся в результате разложения в ряд по :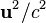

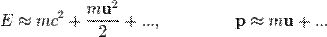
При нулевой скорости энергия частицы называется энергией покоя: 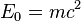. В современной физической литературе принято, что m — масса частицы не зависит от скорости, являясь инвариантом относительно преобразований Лоренца, и является величиной неаддитивной (то есть масса тела, состоящего из нескольких частей, в отличие от классической механики, не равна сумме масс этих частей). Понятие «релятивистской массы», зависящей от скорости 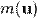не используется, хотя оно и встречается в ранних работах по теории относительности. Историческая причина введения этого понятия была связана с попытками сохранить для релятивистского импульса классическую форму: .

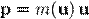При приближении скорости тела к скорости света его энергия и импульс стремятся к бесконечности. Это одна из причин, по которой «обычные» объекты не способны двигаться быстрее скорости света. Для частицы с ненулевой массой даже достижение скорости света потребует затраты бесконечной энергии. Заметные отклонения от классических выражений для энергии и импульса происходят при скоростях, близких к скорости света. Если скорости относительно невелики, то отклонения от классической динамики незначительны. Например, при скорости u=c/4 относительная разница релятивистского и классического импульса составляет всего 3 %.

Между релятивистской энергией и импульсом существуют следующие связи:

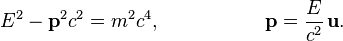
Эти формулы остаются справедливыми и для объектов, движущихся со скоростью света. В этом случае их масса покоя должна быть равна нулю .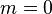

Преобразования энергии и импульса

Аналогично преобразованиям Лоренца для времени и координат релятивистские энергия и импульс, измеренные относительно различных инерциальных систем отсчёта, связаны аналогичными соотношениями:

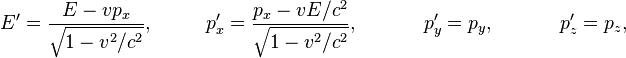
где компоненты вектора импульса 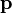равны 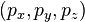. Относительная скорость и ориентация инерциальных систем отсчёта S, S' определены так же, как и в преобразованиях Лоренца.

20)

Идеальный газ — математическая модель газа, в которой в рамках молекулярно-кинетической теории предполагается, что: 1)потенциальной энергией взаимодействия частиц, составляющих газ, можно пренебречь по сравнению с их кинетической энергией; 2) суммарный объём частиц газа пренебрежимо мал; 3) между частицами не действуют силы притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги; 4) время взаимодействия между частицами пренебрежимо мало по сравнению со средним временем между столкновениями. В рамках термодинамики идеальным называется газ, подчиняющийся термическому уравнению состояния Клапейрона — Менделеева.

Молекулярно-кинетическая теория (сокращённо МКТ) — теория, возникшая в XIX веке и рассматривающая строение вещества, в основном газов, с точки зрения трёх основных приближенно верных положений:

• все тела состоят из частиц: атомов и молекул;
• частицы находятся в непрерывном хаотическом движении (тепловом);
• частицы взаимодействуют друг с другом путём абсолютно упругих столкновений.

Основное уравнение МКТ связывает макроскопические параметры (давление, объём, температура) термодинамической системы с микроскопическими (масса молекул, средняя скорость их движения).