Электрические колебания и волны

Законы Ома и их обобщение

При прохождении тока через проводники 2-го класса на электродах происходит выделение вещества (химические процессы) – электролиз. Прохождение тока в растворах объясняется появлением ионов. Распад молекул на ионы называется электролитической диссоциацией, он происходит при растворении вещества. Теория электролитической диссоциации разработана Р. Клаузиусом (1857 г.) и разработана С. Аррениусом (1887 г.). Большое значение имеют также работы русского ученого И.А. Каблукова.

Наряду с диссоциацией при соударениях возможны обратные процессы воссоединения разноименных ионов в нейтральные молекулы – рекомбинация или молизация.

Способность диссоциировать у различных жидкостей – различна. Для количественной характеристики степени диссоциации вводится коэффициент степень диссоциации α.

α – определяется соотношением числа диссоциированных молекул, т.е. он показывает – какая доля молекул растворенного вещества распалась на ионы.

α зависит: от природы растворителя; от природы растворяемого вещества;от концентрации раствора; от температуры. Электрический ток в жидкостях обусловлен упорядоченным движением ионов. При отсутствии внешнего поля ионы в электролите совершают тепловое движение. При перемещение иона возникает сила трения, пропорциональная средней скорости движения иона: 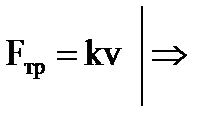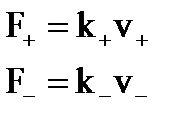, где k – коэффициент трения.

С другой стороны движение иона происходит под действием электрической силы:

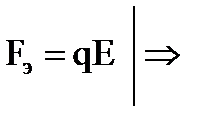
Для установившегося режима:

,

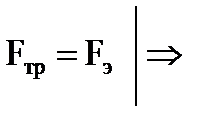
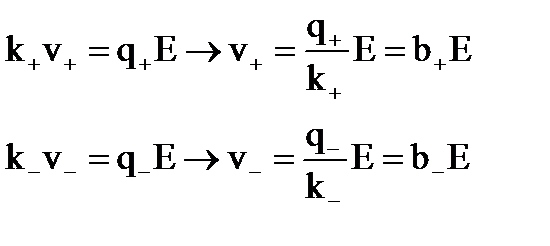где b – подвижность ионов.

Подвижность – скорость ионов при Е=1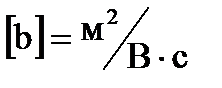

Плотность тока в электролите равна:

j = j₊ + j_– ,

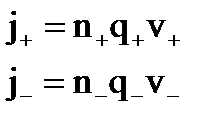где n – концентрация ионов. Для бинарных электролитов справедливо:n₊ = n_– = an,где a – коэффициент диссоциации;n – число молекул растворенного вещества в единице объема электролита. Полагая также q₊ = q_– = q, имеем:j = αnqv₊ + αnqv_– = αnq(v₊ + v_–)

Учитывая, что v₊ = b₊E; v_– = b_–E 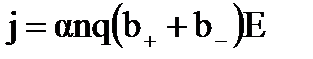–закон Ома для электролитов. Сравнивая эту формулу с дифференциальной формой закона Ома j = gE, получим: γ = anq(b₊ + b_–).

Плотность тока в металле под действием поля Е: 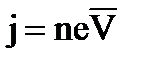, где – средняя скорость упорядоченного движения. Сила, действующая на электрон: ,

где V_т – максимальная скорость в конце λ, следовательно, средняя скорость: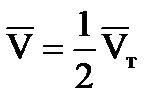

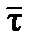– среднее время между соударениями,

Итак, имеем: 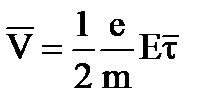Подставляя τ из уравнения, получим: 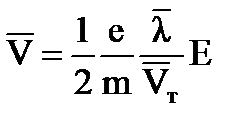. Зная что 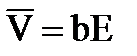, где b – подвижность,и меем: 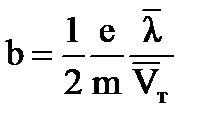Подставляя в уравнение получим:

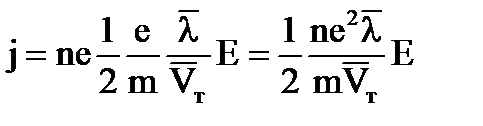, откуда: 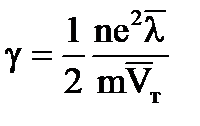(закон Ома)

j = γE, где j – удельная электропроводность.

Вывод: 1) γ тем больше, чем больше n и 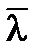; при увеличении Т, а, следовательно, и 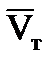, сопротивление R увеличивается.

Резонанс

Резонансом называется явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы (или, в случае электрических колебаний, частоты вынуждающего переменного напряжения) к частоте, равной или близкой собственной частоте колебательной системы. Амплитуда вынужденных колебаний имеет максимум при частоте 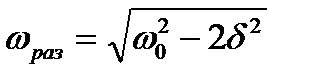, которая называется резонансной частотой.