Внутреннее трение (вязкость)

Вследствие хаотического теплового движения молекул происходит обмен молекулами между слоями газа движущимися с различными скоростями, в результате чего импульс слоя, движущегося быстрее, уменьшается, а движущегося медленнее – увеличивается (происходит перенос импульса от одного слоя к другому). Это приводит к торможению слоя, движущегося быстрее, и ускорению слоя, движущегося медленнее.

Сила внутреннего трения, возникающая в плоскости соприкосновения двух скользящих относительно друг друга слоев, пропорциональна площади из соприкосновения ∆S и градиенту скорости ∆ω/∆х (закон Ньютона).

Коэффициент внутреннего трения не зависит от давления, так как пропорционален произведению <λ>ρ (<λ>- уменьшается, а ρ – увеличивается при возрастании давления).

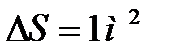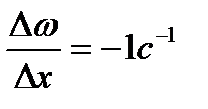Если в формуле принять и , то .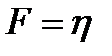

То есть вязкость численно равна силе внутреннего трения, действующей на 1м² площади соприкосновения параллельно движущихся слоев газа при градиенте скорости -1с^-1.

Внешнее сходство математических выражений, описывающих явления переноса, обусловлено общностью лежащего в основе явлений теплопроводности, диффузии и внутреннего трения молекулярного механизма перемешивания молекул в процессе их хаотического движения.

Теплота и температура

Беспорядочное движение микроскопических частиц связано с содержанием в веществе теплоты – особой формы энергии. Эта связь достаточно очевидна на примере зависимости броуновского движения от количества сообщенного телу тепла. Макроскопическая характеристика теплового движения – температура. Температура есть мера содержащегося в теле тепла. Она же определяет направление перехода тепла – от более нагретого тела к менее нагретому. Если температуры тел одинаковы, то передачи тепла от одного тела к другому не происходит. Рассматривая теплоту как форму энергии, необходимо связать ее с кинетической энергией частиц. Чем больше нагрето тело, тем больше и кинетическая энергия его частиц. Таким образом, кинетическую энергию движения частиц так же, как и температуру, можно рассматривать как меру теплового движения. Температура — это макроскопическая характеристика тела, т. е. термодинамическая переменная, в то время как кинетическая энергия характеризует отдельную частицу. Поэтому температура должна быть связана со средней кинетической энергией, приходящейся на одну частицу в системе большого числа частиц. Среднюю кинетическую энергию частиц в системе, состоящей из N частиц, обозначим через <E_k> и определим ее следующим образом: 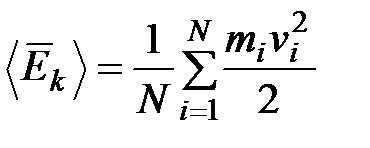.Если все частицы одинаковы, массу частицы можно вынести из-под знака суммы: 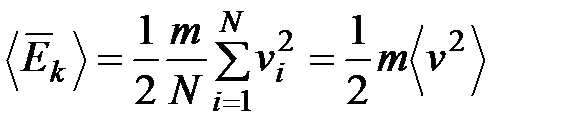.Будем считать что температура T ~ 2<E_k>/3 = m<v²>/3.

Для того чтобы выразить температуру в градусах, нужно ввести коэффициент пропорциональности, показывающий, сколько джоулей соответствует одному градусу. Он называется постоянной Больцмана и, как показывают измерения, равен 1,38·10^‑23 Дж/К, где К означает градус Кельвина – единицу измерения температуры, используемую в физической шкале. Тогда соотношение между температурой в градусах и энергией в джоулях запишется в виде: 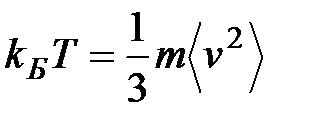или .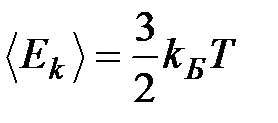

Принятая в физике шкала температур называется абсолютной шкалой, или шкалой Кельвина. В этой шкале температура замерзания воды, то есть 0°С, соответствует 273,15 градусов Кельвина, что обозначается 273,15 К. При T = 0 всякое тепловое движение частиц в веществе прекращается. Эта температура имеет название абсолютного нуля.Подчеркнем статистический характер определения температуры, поскольку она связана со средней энергией частиц. Поэтому можно говорить лишь о температуре системы достаточно большого числа частиц – макроскопической системы, и нельзя говорить о температуре одной или, допустим, десяти частиц. В процессе измерения температуры происходит обмен теплом между частицами– объектом измерения и измерительным прибором – термометром. Понятие температуры тела приобретает смысл в том случае, если обмен теплом между телом и прибором в процессе измерения температуры мало изменяет состояние тела.

Внутренняя энергия газа

Внутренней энергией тела называют часть его полной энергии за вычетом кинетической энергии движения тела как целого и потенциальной энергии тела во внешнем поле. Таким образом, во внутреннюю энергию входят кинетическая энергия поступательного и вращательного движений молекул, потенциальная энергия их взаимодействия, энергия колебательного движения атомов в молекулах, а также энергия различных видов движения частиц в атомах. В идеальном газе потенциальная энергия взаимодействия молекул пренебрежимо мала и внутренняя энергия равна сумме энергий отдельных молекул 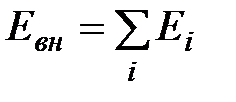,где E_i– энергия отдельной молекулы. До сих пор мы пользовались представлением о молекулах как о материальных точках. Кинетическая энергия молекул считалась совпадающей с энергией их поступательного движения, а средняя кинетическая энергия молекулы полагалась равной 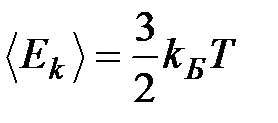. Эта энергия распределяется между тремя поступательными степенями свободы.

Ввиду полной беспорядочности движения молекул в газе все направления перемещения молекулы равновероятны. Поэтому на каждую степень свободы поступательного движения приходится в среднем энергия 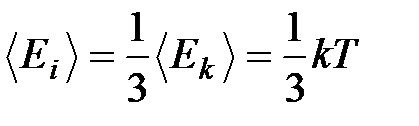.Представление о молекулах как о материальных точках оправдывается только для одноатомных газов. В случае многоатомных газов нужно рассматривать молекулы как сложные системы, способные вращаться как целое, причем атомы в них могут совершать колебания вблизи своих положений равновесия. Общее число степеней свободы молекулы при этом увеличивается.

Положение абсолютно твердого тела можно определить, задав три координаты его центра инерции и три угла, характеризующие возможные повороты тела в пространстве. Таким образом, абсолютно твердое тело имеет шесть степеней свободы – три поступательных и три вращательных.

N материальных точек, не связанных между собой, имеют 3N степеней свободы. Поскольку положение в пространстве системы как целого точно так же, как и положение абсолютно твердого тела определяется шестью параметрами, упомянутыми выше, то число степеней свободы такой системы равно 3·N-6. Это число соответствует возможным смещениям точек относительно друг друга около своих положений равновесия. Такой тип движения называется колебательным. Значит, количество колебательных степеней свободы и есть 3·N-6.

Энергия молекул, состоящих из некоторого числа атомов, не жестко связанных друг с другом, будет теперь складываться из энергии поступательного движения, вращательной энергии и энергии колебаний E_i= E_поступ+ E_вращ+E_колеб. Средняя энергия молекулы должна равняться: <E_i> = i·k·T, где i – сумма числа поступательных, вращательных и удвоенного числа колебательных степеней свободы молекулы: i= i_поступ+ i_вращат+ 2·i_колеб.

Внутренняя энергия на один моль идеального газа .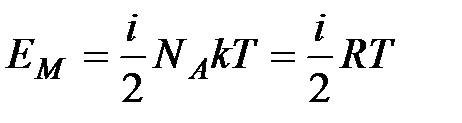

Теплоемкость

Количество тепла, при получении которого температура тела повышается на один градус, называется теплоемкостью. Согласно этому определению 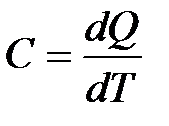. Теплоемкость различается в зависимости от того, при каких условиях происходит нагревание тела – при постоянном объеме или при постоянном давлении. Если нагревание тела происходит при постоянном объеме, т. е. dV = 0, то работа равна нулю. В этом случае передаваемое телу тепло идет только на изменение его внутренней энергии, dQ = dE, и в этом случае теплоемкость равна изменению внутренней энергии при изменении температуры на 1 К, т. е. 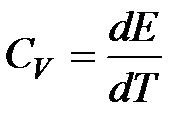. Поскольку для газа 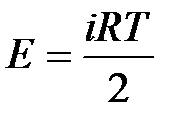, то 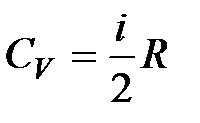. Эта формула определяет теплоемкость 1 моля идеального газа, называемую молярной. При нагревании газа при постоянном давлении его объем меняется, сообщенное телу тепло идет не только на увеличение его внутренней энергии, но и на совершение работы, т.е. dQ = dE + PdV. Теплоемкость при постоянном давлении 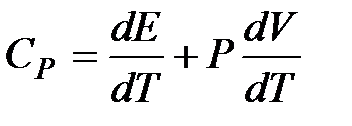. Для идеального газа PV = RT и поэтому PdV = RdT. Учитывая это, найдем 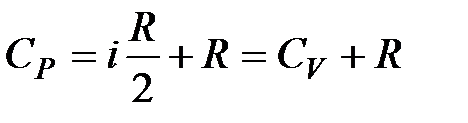.Отношение 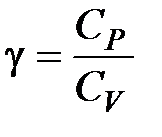представляет собой величину, характерную для каждого газа и определяемую числом степеней свободы молекул газа.

Явления переноса

Явлениями переноса называются необратимые процессы в термодинамически неравновесных системах, в которых происходит пространственный перенос энергии (теплопроводность), массы (диффузия), импульса (внутреннее трение). Для простоты ограничимся одномерными случаями, выбрав ось x так, чтобы она была направлена в направлении переноса. 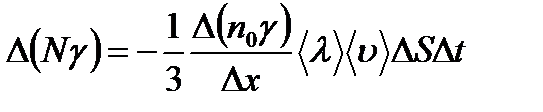.