Сложение взаимно перпендикулярных колебаний
Рассмотримx = Acos(wt + φ10); y = Bcos(wt + φ20 ), предположим φ10, φ 20 = 0 и поделим эти уравненияx / y = A / B → y = (B / A)x - уравнение р=прямой.
Если φ 20 = φ10 + π то cos меняет знак иy = - (B / A)x
Пустьφ 20 = φ10 + π/2; x / A = cos(wt + φ10); y / B = cos[(wt + φ10) + π/2] = sin(wt + φ10) Возводя полученное в квадрат и складывая x2 / A2 + y2 / B2 = cos2(wt + φ10) + sin2(wt + φ10)
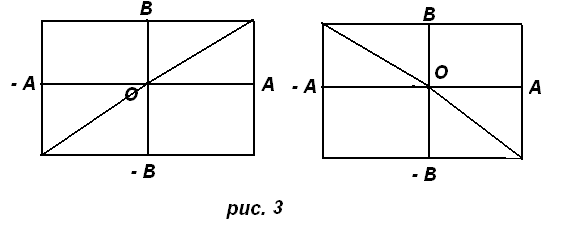
Рисунок 3
Или x2 / A2 + y2 / B2 = 1 – это уравнение эллипса.
При A = B – окружность. При произвольных φ10 и φ20 будет эллипс, нос наклоном.
Сложение двух одинаково направленных колебаний
Одинаковой амплитуды с мало отличающимися частотами
В этом случае разность фаз переменная. Примем за начало отсчета момент времени, когда она равна нулю (φ01-φ02). Уравнения слагаемых колебаний имеют вид:
; 
.
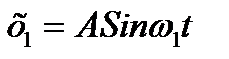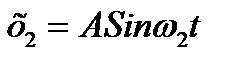Смещение результирующего колебания равно
.
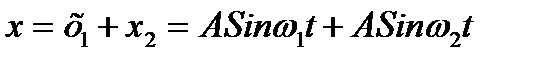Применяя тригонометрическую формулу преобразования суммы синусов получим
.
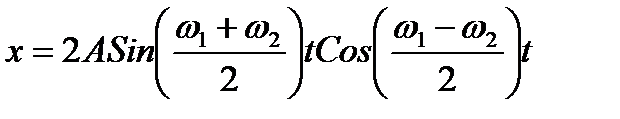Такое колебание не является гармоническим. Амплитуда медленно периодически изменяется во времени (круговая частота амплитуды мала, а период большой). Такие колебания называются биениями. Сначала фазы колебаний одинаковы. Затем одно из колебаний постепенно отстает по фазе от другого, и амплитуда результирующего колебания уменьшается до нуля при разности фаз π.
Сложение сонаправленных гармонических колебаний одинаковой частоты
Результирующее смещение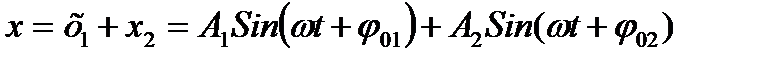 
.Амплитуда результирующего колебания максимальна и равна сумме амплитуд слагаемых колебаний (разность фаз – четное число π) и их разности (разность фаз – нечетное число π).
При одинаковых амплитудах слагаемых результирующая амплитуда либо удваивается, либо колебания компенсируют друг друга.
Сложение встречных волн одинаковой частоты и амплитуды
Важным практическим случаем является интерференция двух когерентных волн распространяющихся навстречу друг другу, уравнения которых имеют вид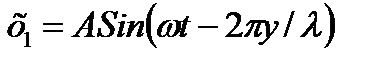 
; 
.
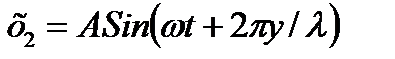Уравнение результирующей волны будет
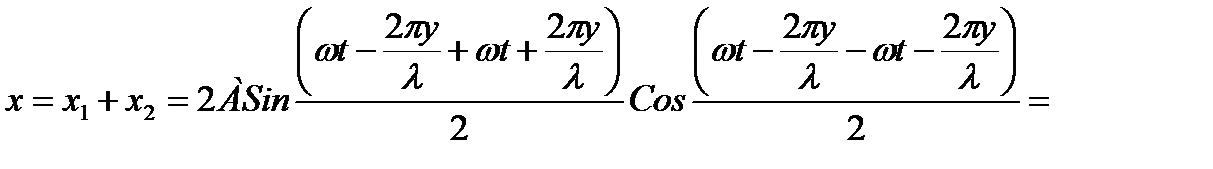
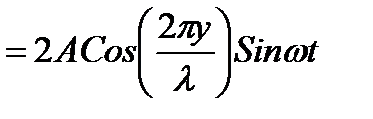.Результирующая волна, которая получается из наложения двух встречных когерентных волн с одинаковой амплитудой называется стоячей – узлы и пучности все время находятся на одном месте. Стоячая волна неподвижна и не переносит энергии вследствие компенсации энергий переносимых встречными волнами.
Звук и его восприятие
Звуковыми (акустическими) волнами называются волны в упругой среде, воспринимаемые слуховым органом человека и животных. Скорость распространения звуковых волн зависит от свойств среды (в газах 0,2-1,2 км/с, в жидкостях 1,2-2 км/с, в твердых телах 2-5 км/с). Человек может воспринимать волны в диапазоне 20-20000 Гц. Для того, чтобы звуковая волна была воспринята, необходимо, чтобы она обладала достаточной интенсивностью, превышающей, так называемый порог слышимости. Звук, который ниже порога слышимости не воспринимается. Звук слишком большой интенсивности вызывает болевые ощущения. Максимальное значение интенсивности, превышение которого вызывает болевые ощущения, называется болевым порогом. Значения порогов различны для частот.
Ухо наиболее чувствительно к частотам 1-3 кГц, для которых порог слышимости 10-12 Вт/м2, а болевой порог составляет 1026 Вт/м2. Субъективное восприятие характеризуется высотой, тембром и уровнем громкости. Ультразвук широко применяется для диагностики и в физиотерапии, а также химиотератии и биотехнологии.
Вопросы для самоконтроля:
1) Что называется амплитудой колебаний?
2) Два гармонических колебания при сложении погасились. Охарактеризуйте их (направления, амплитуды, частоты и фазы).
3) Что называется волной и какими параметрами она характеризуется?
4) Что называется длиной волны? Разностью хода волн? Что такое фронт волны?
5) Каким образом создаются стоячие волны?
6) Каков диапазон частот звуковых волн? Может ли звук распространяться в вакууме?
Список литературы
Основная
1.Теоретическая механика: Учебник для студентов учреждений высшего профессио-нального образования / С.В. Болотин,[и др.]. – М.: Издательский центр «Академия», 2010 г.- 432 с.
Дополнительная
1. Грабовский, Р.И. Курс физики. 6-е изд. / Р. И. Грабовский. – СПБ. : Издательство «Лань», 2002. – 608 с
Лекция 5