Трехфазная асинхронная машина при неподвижном роторе

Рассмотрим симметричную многофазную асинхронную машину и симметричные режимы ее работы, когда сопротивления фаз каждой обмотки одинаковы, а напряжения и токи обмоток статора и рото­ра составляют симметричные системы прямой последовательности. Кроме этого будем считать, что в воздушном зазоре действуют только основные гармоники поля обеих обмоток. Если асинхронный двигатель имеет трехфазную обмотку ротора, она должна быть зам­кнута на добавочное сопротивление. Пусть ротор асинхронной ма­шины заторможен, обмотка статора включена в трехфазную сеть c фазным напряжением U₁. При этих условиях асинхронная машина работает как трансформатор. Симметричные первичные фазные токи I₁ создают МДC с амплитудой основной гармоники на полюс, рав­ной

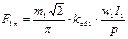, (6)

где k_об1 - обмоточный коэффициент;

w₁ - число последовательно соединенных витков фазы обмотки;

p - число пар полюсов;

m₁ - число фаз обмотки статора.

МДС F₁ обмотки статора создает магнитный поток на полюс Ф₁, амплитудное значение которого равно

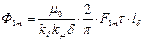, (7)

где μ=4p ·10^-7 Гн/м - магнитная проницаемость воздушного зазора;

δ - воздушный зазор;

k_δ - коэффициент воздушного зазора (Картера), учитываю­щий увеличение магнитного сопротивления воздушного зазора, вызванное наличием пазов на статоре и роторе;

k_μ - коэффициент насыщения зубцовой зоны;

τ - полюсное деление;

l_δ - расчетная длина воздушного зазора.

МДС обмотки статора и созданное ею магнитное поле вращаются с угловой скоростью

ω₁=2πf₁/p, (8)

где f₁ - частота сети.

В обмотке ротора основная гармоника вращающегося магнитно­го поля индуцирует ЭДС, под действием которой в обмотке протекает фазный ток I₂. Этот ток создает МДС F₂, амплитуда основной гармоники которой равна

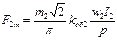, (9)

где m₂ - число фаз обмотки ротора;

k_об2 - обмоточный коэффициент обмотки ротора;

w₂ - число витков фазы.

МДС обмотки ротора F₂ создает магнитный поток на полюс Ф₂, амплитудное значение которого определяется из выражения

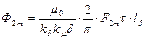, (10)

Магнитные потоки Ф₁ и Ф₂ вращаются с одинаковой угловой скоростью ω₁, и образуют результирующий вращающийся магнит­ный поток Ф. В обмотке статора основная гармоника этого потока наводит ЭДС, действующее значение которой может быть найдено по формуле

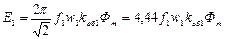, (11)

Это же вращающееся магнитное поле в неподвижной обмотке ротора наводит ЭДС, действующее значение которой равно

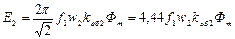. (12) 1.3. Трехфазная асинхронная машина при вращающемся роторе

В асинхронной машине, как и в трансформаторе, имеет место магнитная связь между первичной обмоткой, расположенной на статоре и вторичной обмоткой, расположенной на роторе. Однако, в отличие от трансформатора вторичная обмотка асинхронной машины вращается с угловой скоростью ω и ее проводники перемещаются в магнитном поле, которое в свою очередь вращается с угловой скоростью ω₁. Следовательно, частота ЭДС, тока, величины ин­дуктивных сопротивлений обмотки ротора являются функциями сколь­жения S.

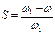, (13)

где ω₁ - угловая скорость вращения поля;

ω - угловая скорость вращения ротора.

Как и при неподвижном роторе, МДС обмотки F₂ при вращении ротора асинхронной машины вращается с той же угловой скоростью ω₁ относительно статора, что и МДС обмотки статора F₁. Дока­жем это.

Пусть асинхронная машина работает в режиме двигателя, и под действием электромагнитного момента ротор вращается с угло­вой скоростью ω в сторону вращения магнитного поля. В этом случае угловая скорость вращения магнитного поля, созданного то­ком обмотки статора относительно проводников обмотки ротора, уменьшается и станет равной

ω₂=ω₁-ω=2πf₂/p. (14)

Из этой формулы найдем выражение для частоты f₂

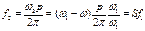Таким образом, частота ЭДC и тока в обмотке ротора пропор­циональна скольжению S. Действующее значение ЭДС вращающегося ротора равно

E_2S=4,44f₂w₂k_об2Ф_m=4,44Sf₁w₂k_об2Ф_m=SE₂, (15)

где E₂ - ЭДC неподвижного ротора (12).

Протекая по обмотке ротора, ток I₂ создает МДС F₂ и магнит­ный поток Ф₂, вращающиеся относительно ротора с угловой скоро­стью ω₂, соответствующей частоте тока в роторе f₂. Но в свою очередь ротор вращается относительно неподвижного статора с уг­ловой скоростью ω. Таким образом, результирующая угловая скорость вращения МДC F₂ и магнитного потока Ф₂ относительно статора определяется как сумма угловых скоростей (ω+ω₂)=ω+ω₁-ω=ω₁. Следовательно, МДС F₂ и магнитный поток Ф₂ обмотки ротора вращаются относительно статора с той же са­мой угловой скоростью, что и МДС F₁ и магнитный поток Ф₁, со­зданные токами обмотки статора. МДС F₁ и F₂ сдвинуты в простран­стве относительно друг друга на такой угол, чтобы получить результирующую синусоидальную волну MДC F₁₀, необходимую для соз­дания основного магнитного потока Ф.

По аналогии с трансформатором получаем

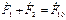(16) Подставим в это уравнение значения МДC по формулам (6) и (9).

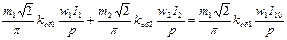, (17)

Из полученного уравнения найдем ток I₁₀

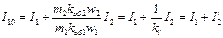, (18)

где I ^/₂= I₂/к_i - ток ротора, приведенный к обмотке статора;

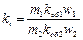- коэффициент приведения токов. (19)

Из уравнения (18) найдем ток обмотки статора асинхронной маши­ны

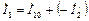, (20) Таким образом, как и в трансформаторе, ток обмотки статора асинхронной машины состоит из двух составляющих: намагничиваю­щего тока İ₁₀, который обусловливает создание вращающегося магнитного поля в зазоре машины, и тока (-İ ^/₂), который компенсирует размагничивающее действие со стороны обмотки ротора.

1.4. Приведение рабочего процесса асинхронной машины при вращающемся роторе к рабочему процессу при неподвижном роторе

Как уже отмечалось в параграфе 1.2. при неподвижном рото­ре асинхронная машина работает в качестве трансформатора, при этом электрическая энергия из первичной цепи посредством магнитного поля передается во вторичную цепь. Электрическая энергия во вторичной цепи неподвижной асинхронной машины преобразуется в тепловую и нагревает машину.

Во вращающейся асинхронной машине, работающей, например, в двигательном режиме, электрическая энергия, потребляемая обмот­кой статора из сети, во вторичной цепи превращается в механиче­скую энергию на валу машины и частично, в тепловую энергию, вы­деляемую на сопротивлениях обмотки ротора.

Исследование режимов работы вращающейся асинхронной машины более сложная задача, чем исследование режимов работы трансфор­матора, так как частоты ЭДС и токов обмоток статора и ротора не равны. По этой причине невозможно непосредственное изображение электрических величин, относящихся к статору и ротору на одной плоскости, так как они будут вращаться с разными угловыми скоро­стями, пропорциональными соответствующим частотам.

C другой стороны, если бы удалось вращающуюся асинхронную машину заменить на эквивалентную ей по энергетическим и электро­магнитным соотношениям машиной с неподвижным ротором, то для исследования асинхронной машины можно было бы применить теорию трансформаторов.

Решение такой задачи возможно, поскольку, как было установ­лено в параграфе 1.3. при вращении ротора МДС и магнитные поля статора и ротора, вращаются с одинаковой угловой скоростью ω₁ и образуют результирующее вращающееся магнитное поле. Но одного этого условия еще недостаточно для приведения режима работы вра­щающейся асинхронной машины и эквивалентному режиму неподвижной машины. Для этого необходимо, чтобы остались неизменными величи­ны токов обмоток и их фазовые сдвиги относительно друг друга. В этом случае остаются неизменными величины результирующих МДС и магнитных потоков, а также величины потребляемой из сети мощно­сти и электромагнитной мощности, передаваемой через зазор с по­мощью магнитного поля от статора в ротор. Кроме того, при пере­ходе к неподвижной машине механическая мощность должна быть представлена равной ей электрической мощностью.

На основании второго закона Кирхгофа составим уравнения на­пряжений для фазы обмоток ротора и статора

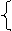
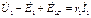
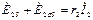(21)

где U₁ - фазное напряжение источника питания (сети);

I₁; I₂; r₁; r₂ – токи и активные сопротивления фаз обмо­ток статора и ротора;

Е₁; Е_2S – действующие значения ЭДС (11) и (15), наводимых основным магнитным потоком Ф;

Е_1σ; E_2σ - действующие значения ЭДС, наводимых потоками рассеяния.

ЭДС рассеяния обмоток статора и ротора можно выразить следующим образом

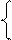
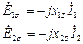(22)

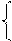где x₁; x_2S - индуктивные сопротивления рассеяния фаз ста­тора и вращающегося ротора, которые равны

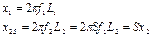, (23)

x₂ - индуктивное сопротивление рассеяния неподвижного ротора;

где L₁, L₂ - индуктивности фаз обмоток статора и ротора от потоков рассеяния Ф_1σ и Ф_2σ. Так как потоки рассеяния обмоток замыкаются, в основном, по воздуху, то будем считать индуктивности L₁ и L₂ величинами по­стоянными.

С учетом выражений для ЭДС рассеяния (22) систему уравнений напряжений (21) представим в виде

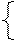
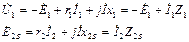(24)

Из второго уравнения системы напряжений найдем ток фазы обмотки ротора

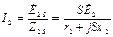(25)

Этому уравнению соответствует схема замещения вращающегося ротора

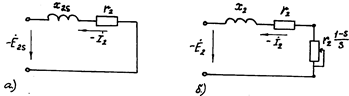
рис. 2а.

Рис.2. Схемы замещения вращающегося (а) и неподвижного (б) ротора

асинхронного двигателя.

Преобразуем выражение для тока ротора (25). Для этого раз­делим числитель и знаменатель на скольжение S, получим выра­жение для тока I₂ в виде

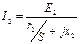, (26)

Новому выражению для тока I₂ соответствует схема замещений рис.2б. В этой схеме замещения (по сравнению со схемой рис.2а) на зажимах вместо ЭДС вращения ротора Е_2S=SE₂ с частотой f₂=Sf₁ действует ЭДС при неподвижном роторе Е₂ с частотой f₁. Соответственно, вместо индуктивного сопротивления x_2S=Sx₂ и активного сопротивления r₂ вращающегося ротора име­ют место индуктивное сопротивление x₂ и активное сопротивление r₂/S неподвижного ротора. Активное сопротивление r₂/S мож­но представить в виде суммы двух сопротивлений r₂/S=r₂+r₂(1-S)/S. Введение добавочного сопротивления r₂(1-S)/S в схему замещения не оказывает влияния на фазу тока ротора I₂ относительно ЭДC Е₂. Действительно, из схем замещения рис.2 имеем

tgψ₂=x_2S/r₂=Sx₂/r₂=x₂/(r₂/S), (27)

Очевидно, что при переходе от схемы замещения асинхронной машины при вращающемся роторе рис.2а к схеме замещения при не­подвижном роторе рис.2б, токи статора I₁ и ротора I₂ остают­ся неизменными по величине и по фазе, следовательно, не изменят­ся величины потребляемой из сети мощности P₁ (1), электромаг­нитная мощность Р_ЭМ (2), механическая мощность Р_МЕХ (3).

P₁ = m₁U₁I₁cosφ₁;

P_ЭМ = P₁ - ΔP_Э1 - ΔP_M1;

P_МЕХ = P_ЭМ - ΔP_Э2 = P₁ - ΔP_Э1 - ΔPЭ2-ΔPM1.

Так как в эквивалентном режиме при неподвижном роторе потери в статоре и роторе остаются такими же, как во вращающейся асинхронной машине, то мощность, потребляемая в добавочном сопротив­лении r₂(1-S)/S, равна полной механической мощности P_МЕХ, развиваемой асинхронной машиной при вращении

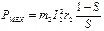, (28)