Тригонометрические подстановки.

Следующие интегралы превращаются в тригонометрические выражения при помощи тригонометрических подстановок:

1. 

1. 

1. 

13. Интегрирование иррациональных выражений, рационализирующие подстановки

Функция f(x) называется иррациональной, если она получена с помощью четырёх рациональных операций (сложения, вычитания, умножения, деления) и возведения в рациональную степень (не целую) переменной интегрирования или некоторого рационального выражения от этой переменной.

Далеко не всегда можно выразить интеграл от иррациональной функции с помощью элементарных функций (интеграл “не берётся” в конечном виде).

Мы рассмотрим некоторые наиболее употребительные иррациональные выражения, неопределённые интегралы от которых могут быть выражены через элементарные функции.

1) Интегрирование выражений R(x,x^m/n,…,x^r/s), где m/n,...,r/s рациональные дроби. Здесь символ R(x,x^m/n,…,x^r/s) означает, что над x,x^m/n,…,x^r/s производятся только рациональные действия (четыре перечисленных выше и возведение в натуральную степень). /“R”=”рациональное выражение от...”/. Пусть k– наименьший общий знаменатель дробей m/n,...,r/s. Осуществим замену X = t^k , тогдаdx = kt^k-1dt.

Каждая дробная степень Xтогда выразится через натуральную степень t и потому

подинтегральное выражение станет рациональной функцией от t. В этой связи замену X = t^k называют рационализирующей подстановкой.

Пример. Вычислить неопределённый интеграл

Решение.Т. к. то наименьший общий знаменатель дробей 1/3и 1/6

будет 6.Потому берём x = t⁶ ,откуда dx = 6t⁵dtи . Тогда

Интегрирование выражений

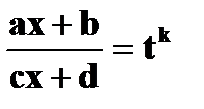Пусть k –наименьший общий знаменатель дробей m/n, … ,r/s.Осуществляя замену

мы сведём интеграл от этого иррационального выражения к интегралу от

рационального выражения по t.

Пример.Вычислить интеграл

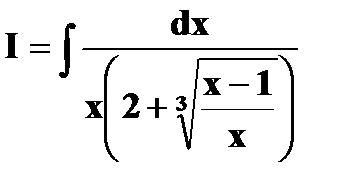
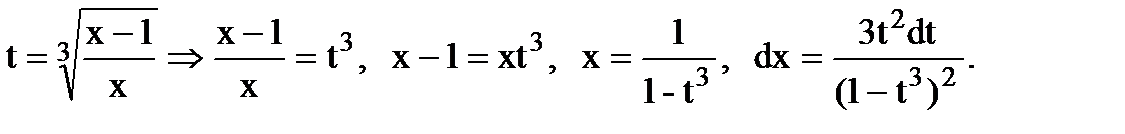
Положим

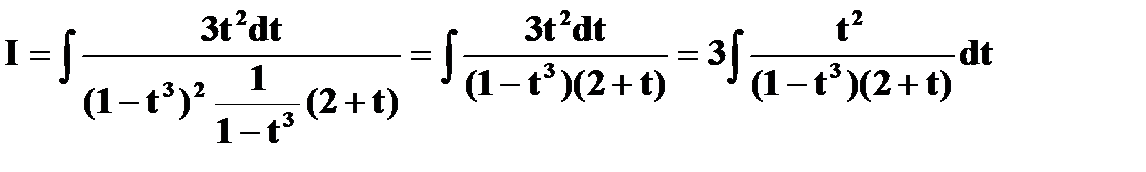
– интеграл от

–

– рациональной. функции.

Разлагаем подинтегральную функцию на простейшие рациональные дроби по методу неопределённых коэффициентов:

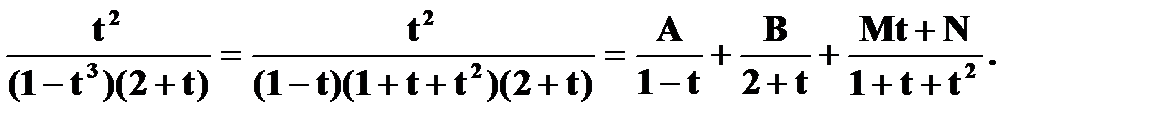
Затем проинтегрируем их и перейдём в результате к первоначальному аргументу x.

14. Задачи, приводящие к понятию определенного интеграла. Определение определенного интеграла, необходимые условия его существования.

Задача о пройденном пути.

Пусть известен закон изменения мгновенной скорости v = v(t). Определим путь, пройденный при движении точки за промежуток времени от t = б до t = в. Движение в общем случае предполагается неравномерным.

Поступим следующим образом.

1). Разобьем весь промежуток времени на n произвольных интервалов

t₀ = б < t₁< t₂ < … < t_i-1 < t_i < … t_n-1 < t_n = в,

где t_i – t_i-1 = Дt_i. На произвольном участке [t_i-1, t_i] будем считать движение близким к равномерному с постоянной скоростью v = v(ф_i), t_i-1 ≤ ф_i ≤ t_i. Тогда за время Дt_i пройденный путь приближенно равен s_i = v(ф_i)Дt_i. Результат справедлив для каждого интервала (i = 1, 2, …, n).

2). Если указанные интервалы достаточно малы, то весь путь приближенно равен сумме:

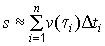
Эта формула тем точнее, чем мельче разбиение данного промежутка времени.

3). Для получения точной формулы пути перейдем к пределу, увеличивая число дроблений (n→∞) и бесконечно измельчая сами интервалы. Обозначим л = Дt_i, тогда

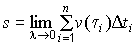
Задача о количестве вещества, вступившего в реакцию.

Пусть скорость химического превращения некоторого вещества, участвующего в химической реакции, есть функция времени v = v(t). Найти количество m вступившего в реакцию вещества за промежуток времени от t₀ до T. Проделаем последовательно те же операции, что и при решении предыдущей задачи. В результате получим:

Работа переменной силы.

Пусть материальная точка под действием постоянной силы F перемещается по направлению этой силы. Если пройденный путь равен s, то, как известно из курса физики, работа Р этой силы F вычисляется по формуле: Р = F_S.

Пусть теперь материальная точка движется по оси Ох от точки А(а) до точки B(b) (b>a) под действием переменной силы, направленной по Ох и являющейся функцией от х: F = f(x).

Для нахождения работы Р в этом случае разобьем отрезок [a; b] точками a = x₀<x₁<…<x_n = b на n частичных отрезков и положим: Дx_i = x_i – x_i-1, i = 1, 2, ..., n. Наибольшую из этих разностей обозначим через л = maxДx_i. Если эти отрезки достаточно малы, то без большой ошибки на каждом из них силу F можно считать постоянной (равной f(ф_i)), что дает приближенное выражение для работы

,

где ф_i – одна из точек сегмента [x_i-1, x_i]. Отсюда:

Задачи о площади криволинейной трапеции.

Пусть на промежутке [a; b] задана функция f(x)≥0. Криволинейной трапецией называется плоская фигура, ограниченная указанной кривой y=f(x), прямыми x=a, x=b и осью Оx. (рис. 1). Для вычисления ее площади проделаем несколько операций.

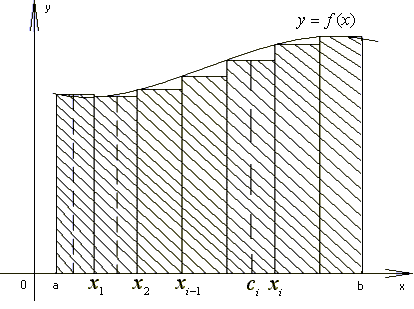
Рис. 1.

1). Разобьем промежуток [a; b] произвольными точками x₀=a<x₁<x₂<…<x_i-1<x_i<…<x_n=b на n частей. Положим Дx_i = x_i – x_i-1, то есть Дx_i есть длина i-го частичного отрезка, а наибольшую из этих длин обозначим л, (л=max Дx_i).

2). На каждом отрезке [x_i-1, x_i] возьмем по произвольной точке c_i,

x_i-1<c_i< x_i и вычислим f(c_i). Построим прямоугольник с основанием [x_i-1, x_i] и высотой f(c_i). Его площадь равна S_i=f(c_i)( x_i – x_i-1). Проделаем это для каждого i = 1, 2, …, n.

3). Площадь всей заштрихованной ступенчатой фигуры, составленной из прямоугольников, равна сумме

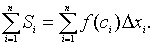
Площадь S криволинейной трапеции будет приближенно равна площади ступенчатой фигуры:

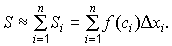
Чем мельче отрезки деления, тем точнее полученная фигура “отображает” криволинейную трапецию.

4). За площадь криволинейной трапеции принимают предел, к которому стремятся площади ступенчатых фигур, когда длины отрезков деления стремятся к нулю, а их число неограниченно увеличивается (n→∞). Таким образом,

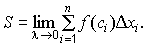
15. Критерий интегрируемости функции (без доказательств). Достаточные условия существования определенного интеграла

Условия интегрируемости функции на отрезке 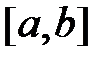– это условия существования определенного интеграла 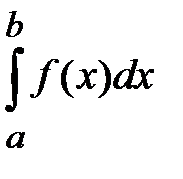. При определении его как предела интегральной суммы предполагалось, что функция 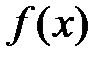ограничена на отрезке .

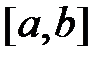Необходимое условие интегрируемости функции

Покажем, что условие ограниченности функций на отрезке 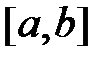является необходимым условием интегрируемости функций, т.е. справедлива следующая теорема.

Т. Если 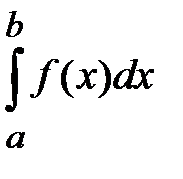существует, то функция 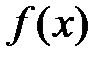ограничена на отрезке .

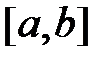Ограниченность является необходимым, но не достаточным условием интегрируемости функции на отрезке 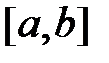, Существуют ограниченные функции, не являющиеся интегрируемыми.

Достаточные условия интегрируемости функции

Т. Если функция 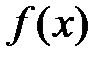непрерывна на отрезке [a, b], то она интегрируема на этом отрезке, т.е. существует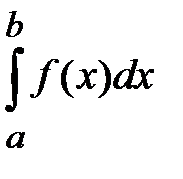

Т. Если функция 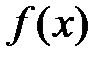ограничена на отрезке [a, b] и непрерывна на нем всюду, кроме конечного числа точек разрыва первого рода, то она интегрируема на этом отрезке.

Т. Если функция 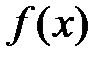монотонна и ограничена на отрезке [a, b], то она интегрируема на [a, b].

Свойства определенного интеграла, выражаемые равенствами

1. Если нижний и верхний пределы интегрирования равны 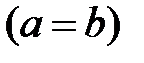, то интеграл равен нулю: .

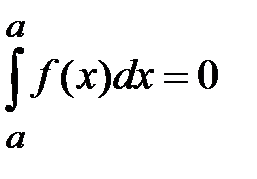2. При перестановке пределов интегрирования определенный интеграл меняет знак на противоположный:

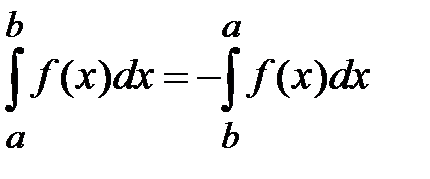
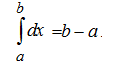
3.

4. Если функция f(x) интегрируема на отрезке [a, b], то и функция 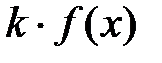, где k – постоянная, также интегрируема на [a, b], причем ,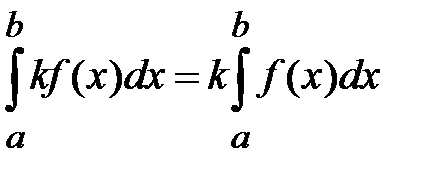

т.е. постоянный множитель можно выносить за знак определенного интеграла.

5. Если функции f(x) и g(x) интегрируемы на [a, b], то 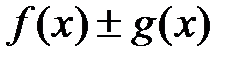также интегрируема на [a, b], причем

.

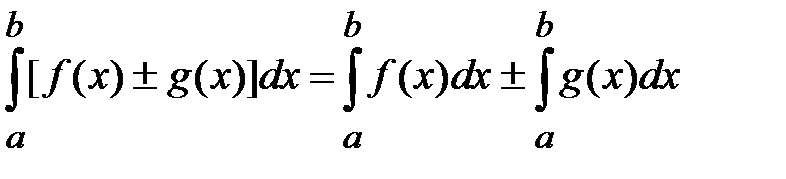6. Аддитивность определенного интеграла. Если существуют интегралы 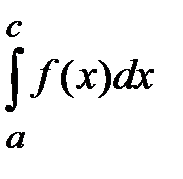и 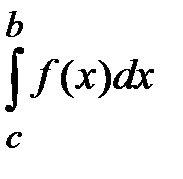, то существует также интеграл 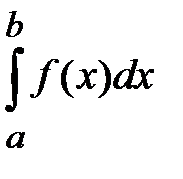(и обратно) и для любых чисел a, b, c .

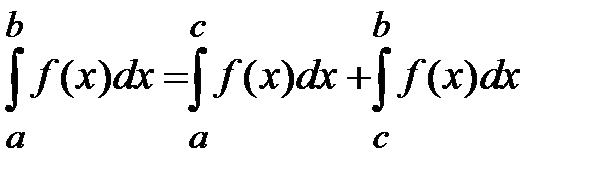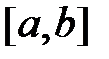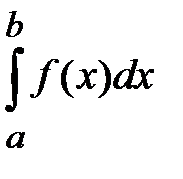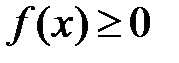
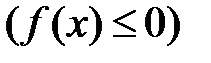
7. Если функция f(x) не меняет знак на , то определенный интеграл сохраняет ее знак, т.е. если 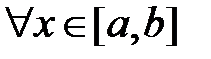, то , , .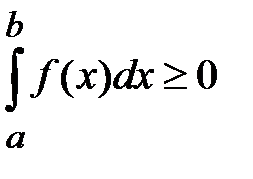

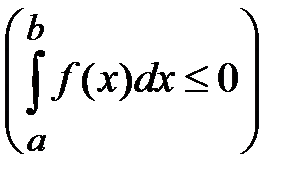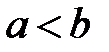8. Монотонность определенного интеграла. Если интегрируемые функци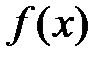и и 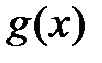удовлетворяют неравенству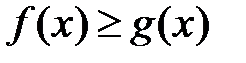 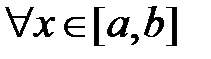, то , .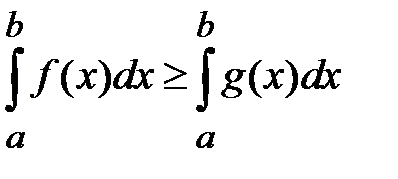

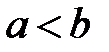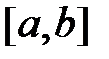
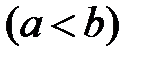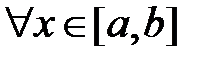
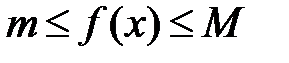9. Оценка интеграла. Если f(x) интегрируема на и , то , .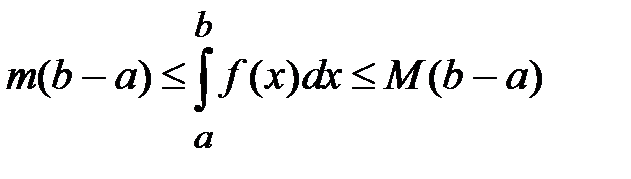

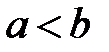10. (о среднем значении для непрерывной функции). Если функция f(x) непрерывна на отрезке 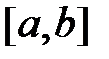, то существует такая точка 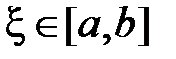, что ,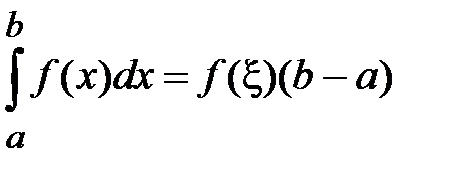

т.е. определенный интеграл от непрерывной функции равен произведению значения подынтегральной функции в некоторой промежуточной точке 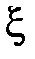отрезка интегрирования 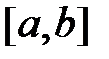и длины b–a этого отрезка.

Число 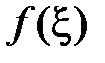, определяемое по формуле 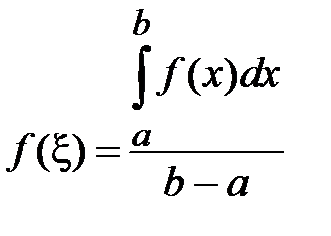, называется интегральным средним значением функции f(x) на отрезке .

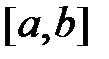16. Основные свойства определенного интеграла

Доопределим понятие определенного интеграла при a ≥ b следующими равенствами:

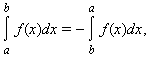
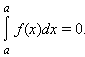
Сформулируем некоторые свойства определенного интеграла в предположении, что подынтегральная функция ограничена на отрезке, по которому она интегрируется.

1). Если функция интегрируема на [a; b], то она интегрируема на

любом отрезке [x₁; x₂] [a; b].

2). Для любых a, b и c

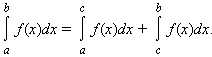
3). Интеграл обладает свойством линейности: для любых функций f(x) и g(x) и любой постоянной A

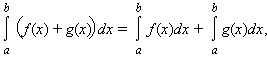
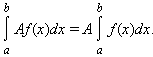
4). Если f(x) и g(x) интегрируемы на [a; b], то f(x) · g(x) также интегрируема на этом отрезке.

5). Если f(x) – периодическая функция с периодом T, то для любого a

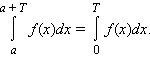
Для определенных интегралов верны также следующие оценки (предполагается, что функции f и g интегрируемы на [a; b]).

1). Если f(x) ≥ g(x), то

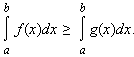
2). В частности, если f(x) ≥ 0, то

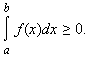
3). Если f(x) ≥ 0 для любого х [a; b] и существует х₀ [a; b] такое, что f(x₀)>0, причем f(x) непрерывна в х₀ то

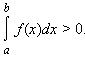
4). |f(x)| интегрируема на [a; b], причем

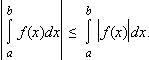
5). Если на отрезке [a; b] m ≤ f(x) ≤ M, то

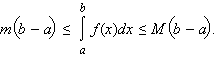
17. Теорема о среднем и ее геометрический смысл