Формула Тейлора с остаточными членами в форме Пеано и Лагранжа
Предварительные сведения из алгебры многочленов
а) Если a вещественный корень многочлена , то существует единственное представление многочлена в виде
P(x) = (x – a)a P1(x), a³1, P1(a)¹0.
Число a называется кратностью корня. Другое эквивалентное определение кратности корня дается в терминах производных: a – это порядок первой, не равной нулю производной в точке a: P(a)= P¢(a)=…= P(a-1)(a)=0, P(a)(a)¹0.
б) Если w = u + i v, v¹0 комплексный корень многочлена с действительными коэффициентами, то сопряженное комплексное число 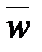 = u - i v также является корнем многочлена. Это утверждение следует из свойств операции комплексного сопряжения:
= u - i v также является корнем многочлена. Это утверждение следует из свойств операции комплексного сопряжения: 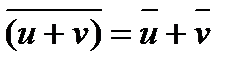 ,
, 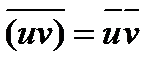 , для действительного числа x справедливо равенство
, для действительного числа x справедливо равенство 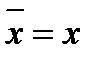 . Поэтому, если w корень многочлена P(x) = a0+…+akxk+…+ anxn , то
. Поэтому, если w корень многочлена P(x) = a0+…+akxk+…+ anxn , то 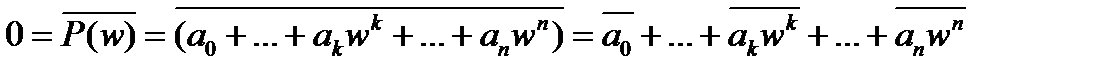 =
= 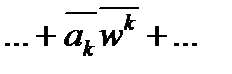 =
= 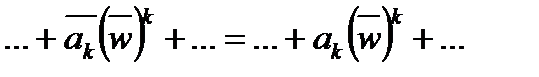 =P(
=P( 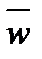 ).
).
Тогда существует единственное представление многочлена в виде
P(x) = (x2+px+q)b P1(x), b³1, P1(w)¹0,
(x - w)(x - 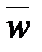 )=(x - u - i v)(x - u + i v)=(x-u)2+v2=x2-2ux+u2+v2= x2+px+q.
)=(x - u - i v)(x - u + i v)=(x-u)2+v2=x2-2ux+u2+v2= x2+px+q.
в) Любой многочлен можно разложить в произведение по своим корням
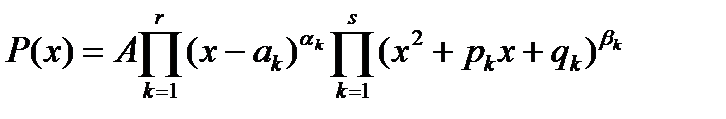 ,
,
где A – старший коэффициент многочлена, a1,a2,…, ar -действительные корни кратностей a1,a2,…, ar , а w1,w2,…, ws комплексные корни кратностей b1,b2,…, bs. Связь между комплексными корнями и сомножителями в разложении многочлена следующая x2+pkx+qk=(x - wk)(x - 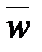 k).
k).
Определение. Рациональная функция ( отношение двух многочленов) 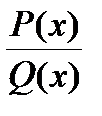 ) называется правильной дробью, если порядок многочлена числителя строго меньше порядка многочлена в знаменателе.
) называется правильной дробью, если порядок многочлена числителя строго меньше порядка многочлена в знаменателе.
Утверждение. Любую рациональную функцию можно представить в виде многочлена (целая часть) плюс правильная дробь .
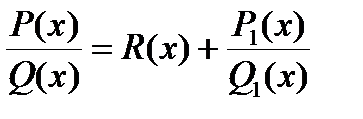 , - R(x) – многочлен, дробь
, - R(x) – многочлен, дробь 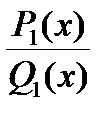 - правильная.
- правильная.
R(x) –называется целой частью, а дробь P1/Q1 –остатком. Остаток и целую часть можно получить делением «уголком».
Пример: 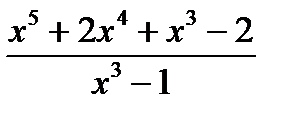

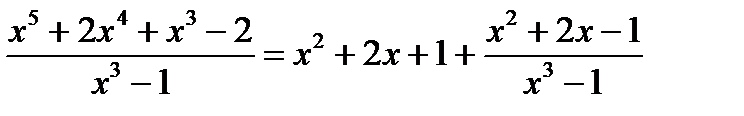
Метод неопределенных коэффициентов
Для нахождения коэффициентов разложения (*) выписывают это разложение с неопределенными коэффициентами, приводят правую и левую часть к общему знаменателю. В полученном равенстве для числителей приравнивают коэффициенты при одинаковых степенях x. В результате получают систему уравнений для определения коэффициентов разложения.
Пример. 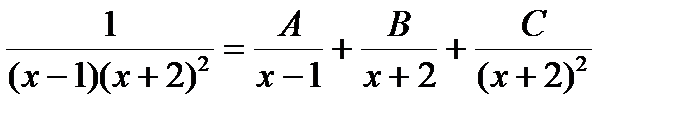
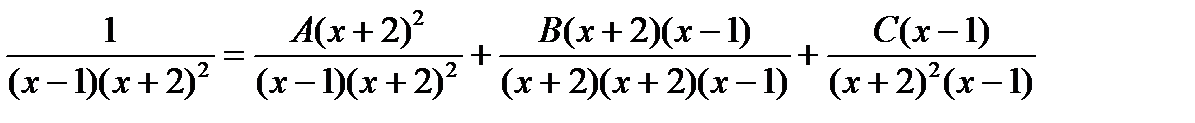
1 = A(x2+4x+4)+B(x2+x-2)+C(x-1)
A+B=0
4A+B+C=0
4A-2B-C=1,
A=-B, 3A+C=0,6A-C=1, A=1/9, B=-1/9, C=-1/3.
Интегрирование выражений
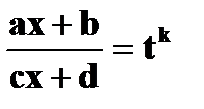 Пусть k –наименьший общий знаменатель дробей m/n, … ,r/s.Осуществляя замену
Пусть k –наименьший общий знаменатель дробей m/n, … ,r/s.Осуществляя замену
мы сведём интеграл от этого иррационального выражения к интегралу от
рационального выражения по t.
Пример.Вычислить интеграл
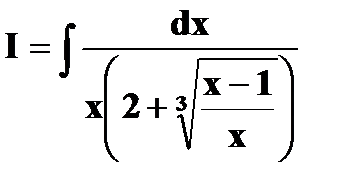
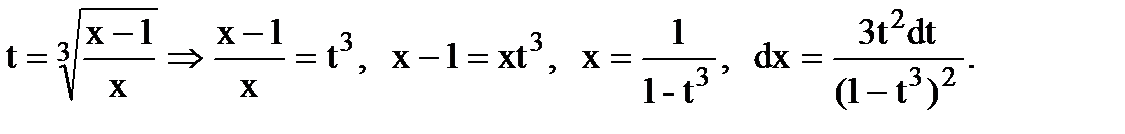
Положим
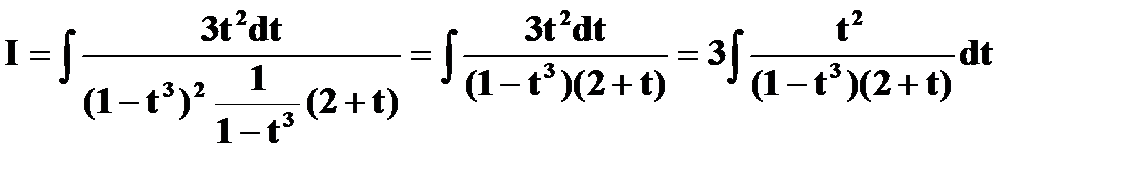
– интеграл от
–
– рациональной. функции.
Разлагаем подинтегральную функцию на простейшие рациональные дроби по методу неопределённых коэффициентов:
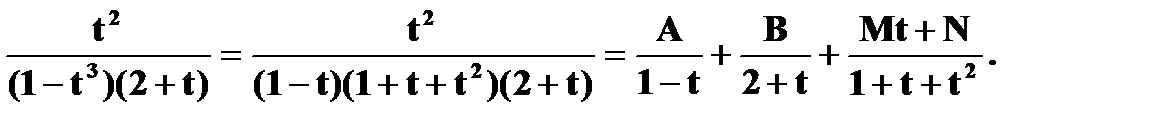
Затем проинтегрируем их и перейдём в результате к первоначальному аргументу x.
14. Задачи, приводящие к понятию определенного интеграла. Определение определенного интеграла, необходимые условия его существования.
Задача о пройденном пути.
Пусть известен закон изменения мгновенной скорости v = v(t). Определим путь, пройденный при движении точки за промежуток времени от t = б до t = в. Движение в общем случае предполагается неравномерным.
Поступим следующим образом.
1). Разобьем весь промежуток времени на n произвольных интервалов
t0 = б < t1< t2 < … < ti-1 < ti < … tn-1 < tn = в,
где ti – ti-1 = Дti. На произвольном участке [ti-1, ti] будем считать движение близким к равномерному с постоянной скоростью v = v(фi), ti-1 ≤ фi ≤ ti. Тогда за время Дti пройденный путь приближенно равен si = v(фi)Дti. Результат справедлив для каждого интервала (i = 1, 2, …, n).
2). Если указанные интервалы достаточно малы, то весь путь приближенно равен сумме:
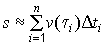
Эта формула тем точнее, чем мельче разбиение данного промежутка времени.
3). Для получения точной формулы пути перейдем к пределу, увеличивая число дроблений (n→∞) и бесконечно измельчая сами интервалы. Обозначим л = Дti, тогда
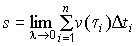
Задача о количестве вещества, вступившего в реакцию.
Пусть скорость химического превращения некоторого вещества, участвующего в химической реакции, есть функция времени v = v(t). Найти количество m вступившего в реакцию вещества за промежуток времени от t0 до T. Проделаем последовательно те же операции, что и при решении предыдущей задачи. В результате получим:
Работа переменной силы.
Пусть материальная точка под действием постоянной силы F перемещается по направлению этой силы. Если пройденный путь равен s, то, как известно из курса физики, работа Р этой силы F вычисляется по формуле: Р = FS.
Пусть теперь материальная точка движется по оси Ох от точки А(а) до точки B(b) (b>a) под действием переменной силы, направленной по Ох и являющейся функцией от х: F = f(x).
Для нахождения работы Р в этом случае разобьем отрезок [a; b] точками a = x0<x1<…<xn = b на n частичных отрезков и положим: Дxi = xi – xi-1, i = 1, 2, ..., n. Наибольшую из этих разностей обозначим через л = maxДxi. Если эти отрезки достаточно малы, то без большой ошибки на каждом из них силу F можно считать постоянной (равной f(фi)), что дает приближенное выражение для работы
,
где фi – одна из точек сегмента [xi-1, xi]. Отсюда:
Задачи о площади криволинейной трапеции.
Пусть на промежутке [a; b] задана функция f(x)≥0. Криволинейной трапецией называется плоская фигура, ограниченная указанной кривой y=f(x), прямыми x=a, x=b и осью Оx. (рис. 1). Для вычисления ее площади проделаем несколько операций.
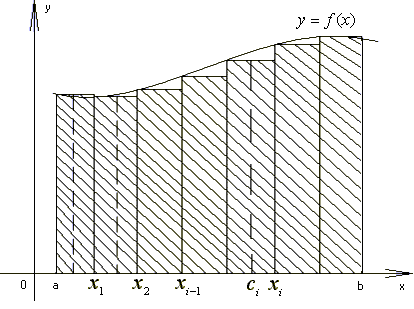
Рис. 1.
1). Разобьем промежуток [a; b] произвольными точками x0=a<x1<x2<…<xi-1<xi<…<xn=b на n частей. Положим Дxi = xi – xi-1, то есть Дxi есть длина i-го частичного отрезка, а наибольшую из этих длин обозначим л, (л=max Дxi).
2). На каждом отрезке [xi-1, xi] возьмем по произвольной точке ci,
xi-1<ci< xi и вычислим f(ci). Построим прямоугольник с основанием [xi-1, xi] и высотой f(ci). Его площадь равна Si=f(ci)( xi – xi-1). Проделаем это для каждого i = 1, 2, …, n.
3). Площадь всей заштрихованной ступенчатой фигуры, составленной из прямоугольников, равна сумме
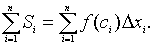
Площадь S криволинейной трапеции будет приближенно равна площади ступенчатой фигуры:
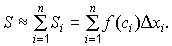
Чем мельче отрезки деления, тем точнее полученная фигура “отображает” криволинейную трапецию.
4). За площадь криволинейной трапеции принимают предел, к которому стремятся площади ступенчатых фигур, когда длины отрезков деления стремятся к нулю, а их число неограниченно увеличивается (n→∞). Таким образом,
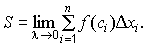
15. Критерий интегрируемости функции (без доказательств). Достаточные условия существования определенного интеграла
Условия интегрируемости функции на отрезке 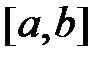 – это условия существования определенного интеграла
– это условия существования определенного интеграла 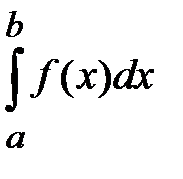 . При определении его как предела интегральной суммы предполагалось, что функция
. При определении его как предела интегральной суммы предполагалось, что функция 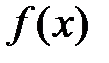 ограничена на отрезке
ограничена на отрезке 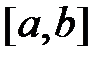 .
.
Необходимое условие интегрируемости функции
Покажем, что условие ограниченности функций на отрезке 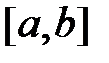 является необходимым условием интегрируемости функций, т.е. справедлива следующая теорема.
является необходимым условием интегрируемости функций, т.е. справедлива следующая теорема.
Т. Если 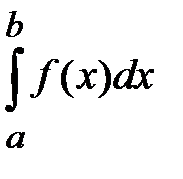 существует, то функция
существует, то функция 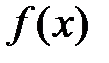 ограничена на отрезке
ограничена на отрезке 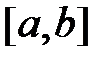 .
.
Ограниченность является необходимым, но не достаточным условием интегрируемости функции на отрезке 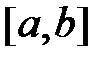 , Существуют ограниченные функции, не являющиеся интегрируемыми.
, Существуют ограниченные функции, не являющиеся интегрируемыми.
Достаточные условия интегрируемости функции
Т. Если функция 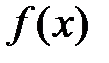 непрерывна на отрезке [a, b], то она интегрируема на этом отрезке, т.е. существует
непрерывна на отрезке [a, b], то она интегрируема на этом отрезке, т.е. существует 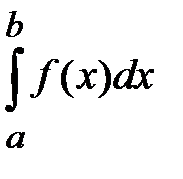
Т. Если функция 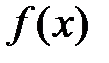 ограничена на отрезке [a, b] и непрерывна на нем всюду, кроме конечного числа точек разрыва первого рода, то она интегрируема на этом отрезке.
ограничена на отрезке [a, b] и непрерывна на нем всюду, кроме конечного числа точек разрыва первого рода, то она интегрируема на этом отрезке.
Т. Если функция 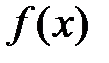 монотонна и ограничена на отрезке [a, b], то она интегрируема на [a, b].
монотонна и ограничена на отрезке [a, b], то она интегрируема на [a, b].
Свойства определенного интеграла, выражаемые равенствами
1. Если нижний и верхний пределы интегрирования равны 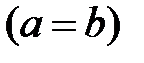 , то интеграл равен нулю:
, то интеграл равен нулю: 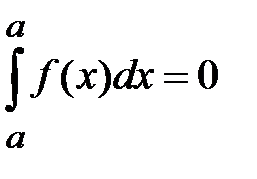 .
.
2. При перестановке пределов интегрирования определенный интеграл меняет знак на противоположный:
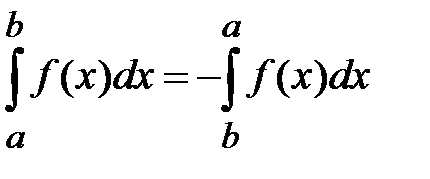
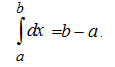
3.
4. Если функция f(x) интегрируема на отрезке [a, b], то и функция 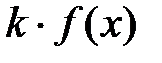 , где k – постоянная, также интегрируема на [a, b], причем
, где k – постоянная, также интегрируема на [a, b], причем 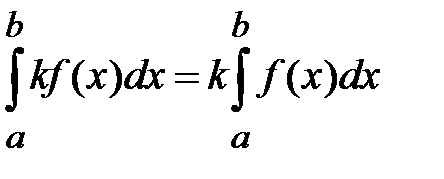
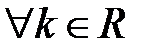 ,
,
т.е. постоянный множитель можно выносить за знак определенного интеграла.
5. Если функции f(x) и g(x) интегрируемы на [a, b], то 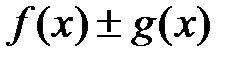 также интегрируема на [a, b], причем
также интегрируема на [a, b], причем
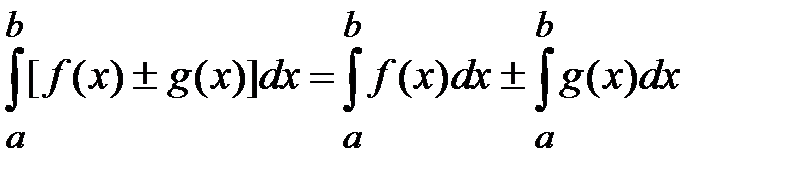 .
.
6. Аддитивность определенного интеграла. Если существуют интегралы 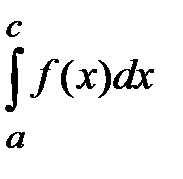 и
и 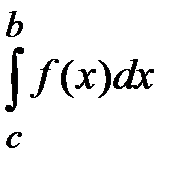 , то существует также интеграл
, то существует также интеграл 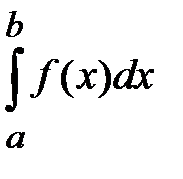 (и обратно) и для любых чисел a, b, c
(и обратно) и для любых чисел a, b, c 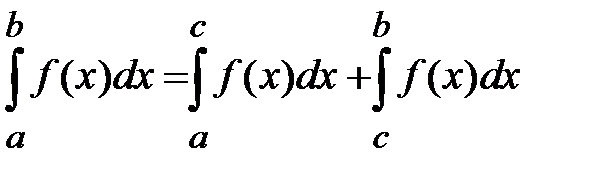 .
.
7. Если функция f(x) не меняет знак на 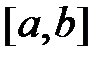 , то определенный интеграл
, то определенный интеграл 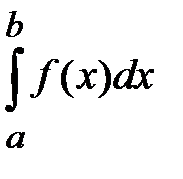 сохраняет ее знак, т.е. если
сохраняет ее знак, т.е. если 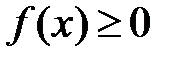
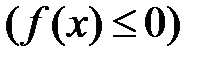
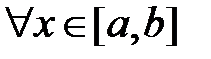 , то
, то 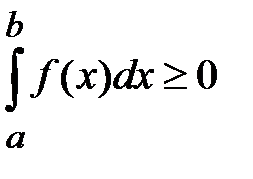 ,
, 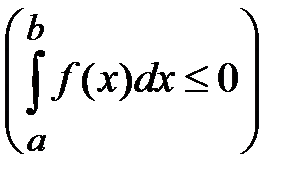 ,
, 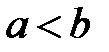 .
.
8. Монотонность определенного интеграла. Если интегрируемые функции 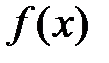 и
и 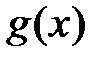 удовлетворяют неравенству
удовлетворяют неравенству 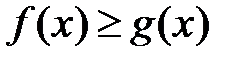
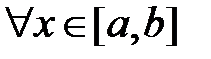 , то
, то 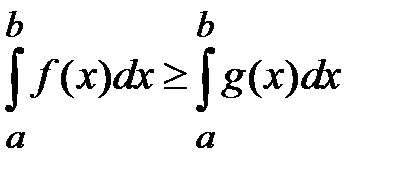 ,
, 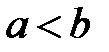 .
.
9. Оценка интеграла. Если f(x) интегрируема на 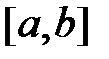
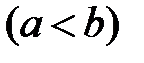 и
и 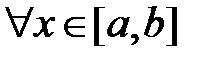
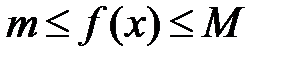 , то
, то 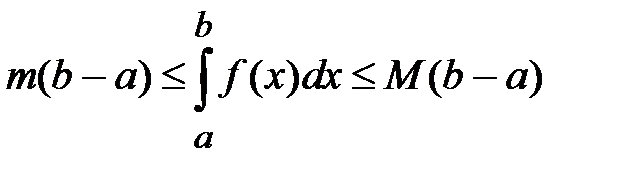 ,
, 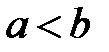 .
.
10. (о среднем значении для непрерывной функции). Если функция f(x) непрерывна на отрезке 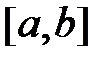 , то существует такая точка
, то существует такая точка 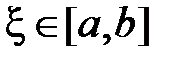 , что
, что 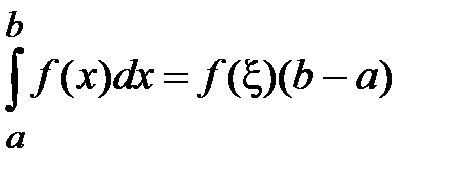 ,
,
т.е. определенный интеграл от непрерывной функции равен произведению значения подынтегральной функции в некоторой промежуточной точке 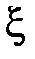 отрезка интегрирования
отрезка интегрирования 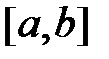 и длины b–a этого отрезка.
и длины b–a этого отрезка.
Число 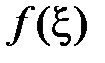 , определяемое по формуле
, определяемое по формуле 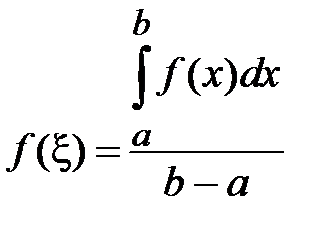 , называется интегральным средним значением функции f(x) на отрезке
, называется интегральным средним значением функции f(x) на отрезке 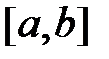 .
.
16. Основные свойства определенного интеграла
Доопределим понятие определенного интеграла при a ≥ b следующими равенствами:
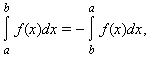
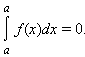
Сформулируем некоторые свойства определенного интеграла в предположении, что подынтегральная функция ограничена на отрезке, по которому она интегрируется.
1). Если функция интегрируема на [a; b], то она интегрируема на
любом отрезке [x1; x2] 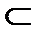 [a; b].
[a; b].
2). Для любых a, b и c
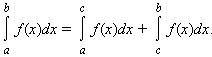
3). Интеграл обладает свойством линейности: для любых функций f(x) и g(x) и любой постоянной A
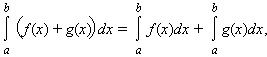
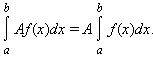
4). Если f(x) и g(x) интегрируемы на [a; b], то f(x) · g(x) также интегрируема на этом отрезке.
5). Если f(x) – периодическая функция с периодом T, то для любого a
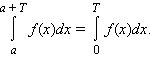
Для определенных интегралов верны также следующие оценки (предполагается, что функции f и g интегрируемы на [a; b]).
1). Если f(x) ≥ g(x), то
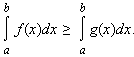
2). В частности, если f(x) ≥ 0, то
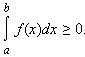
3). Если f(x) ≥ 0 для любого х 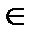 [a; b] и существует х0
[a; b] и существует х0 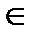 [a; b] такое, что f(x0)>0, причем f(x) непрерывна в х0 то
[a; b] такое, что f(x0)>0, причем f(x) непрерывна в х0 то
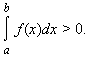
4). |f(x)| интегрируема на [a; b], причем
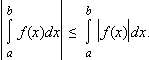
5). Если на отрезке [a; b] m ≤ f(x) ≤ M, то
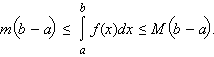
17. Теорема о среднем и ее геометрический смысл
Метод замены переменной
Пусть функция у = f(х) непрерывна на отрезке [a, b], а функция x=φ(t), определена на отрезке [α, β] и имеют на нем непрерывную производную, причем φ (α) = а, φ (β) = b и для всех 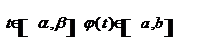 . Тогда
. Тогда
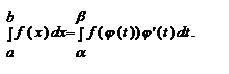
Метод интегрирования по частям
Если функции u = u(x), v = v(x) имеют непрерывные производные на отрезке [a, b], то справедлива формула
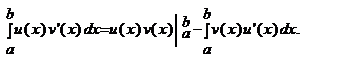 Доказательство.
Доказательство.
Поскольку функция u(x)v(x) – первообразная для функции u’(x)v(x) + u(x)v’(x), то
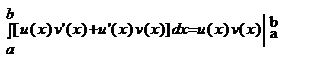
откуда и следует формула 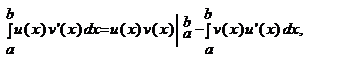 которую можно записать в виде
которую можно записать в виде
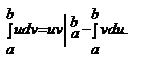
Формула интегрирования по частям для определённого интеграла. Если u(x), v(x) - непрерывно дифференцируемые функции, то 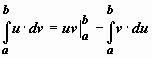 .
.
Необходимое условие интегрируемости.
Если функция интегрируема на отрезке, то она ограничена на нем.
Необходимое и дост. усл. интегрируемости.
Для того, чтобы ограниченная на некотором отрезке функция была интегрируема на нем необходимо и достаточно, чтобы lim∣τ∣→0(Sτ−sτ)=0
20. Понятие площади плоской фигуры, объем тела. Вычисление объема площади плоских фигур и объемов тел вращения
площадь S криволинейной трапеции abAB, ограниченной кривой y=f(x), f(x) 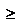 0
0
| y |
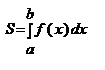
| x |
| b |
| а |
| y=f(x) |
| B |
| A |
| y |
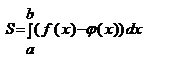
| x |
| A |
| B |
| y=φ(x) |
| C |
| y=f(x) |
| D |
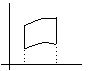
Объем тела, образованного вращением кривой y = f(x), ограниченной прямыми х = а, x = b при a<x<b вокруг оси Ох, вычисляется по формуле:
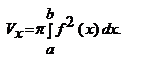
Объем тела, образованного вашей кривой у = φ(у), ограниченной прямымиy = c, y = d при c<y<d вокруг оси Oy, вычисляется по формуле:
Центральный угол — это угол, образованный двумя радиусами. Длина дуги, описываемой концом радиуса, пропорциональна величине соответствующего центрального угла. Центральный угол дуги измеряется градусами. Для измерения градусами - целая окружность имеет 360°. Длина дуги
p=2π r n\360=π r n\180
Определение 3. Тело вращения – это тело, полученное вращением плоской фигуры  вокруг оси, не пересекающей фигуру и лежащей с ней в одной плоскости.
вокруг оси, не пересекающей фигуру и лежащей с ней в одной плоскости.
Ось вращения может и пересекать фигуру, если это ось симметрии фигуры.
Теорема 2. Пусть криволинейная трапеция, ограниченная графиком непрерывной неотрицательной функции 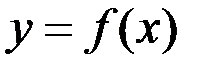 , осью
, осью 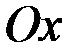 и отрезками прямых
и отрезками прямых 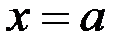 и
и 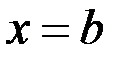
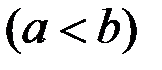 вращается вокруг оси
вращается вокруг оси 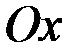 . Тогда объём получающегося тела вращения можно вычислить по формуле
. Тогда объём получающегося тела вращения можно вычислить по формуле
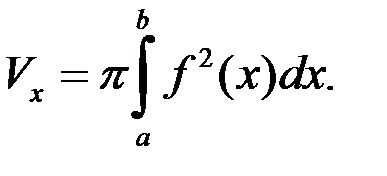 (2)
(2)
Доказательство. Для такого тела сечение с абсциссой 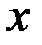 – это круг радиуса
– это круг радиуса 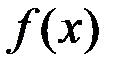 , значит
, значит 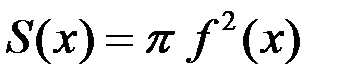 и формула (1) даёт требуемый результат.
и формула (1) даёт требуемый результат.
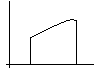
Если фигура ограничена графиками двух непрерывных функций 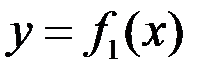 и
и 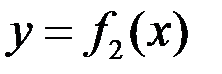 , и отрезками прямых
, и отрезками прямых 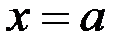 и
и 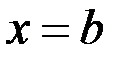 , причём
, причём 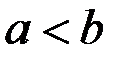 и
и 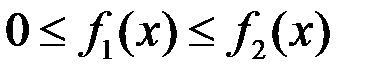 , то при вращении вокруг оси абсцисс получим тело, объём которого
, то при вращении вокруг оси абсцисс получим тело, объём которого
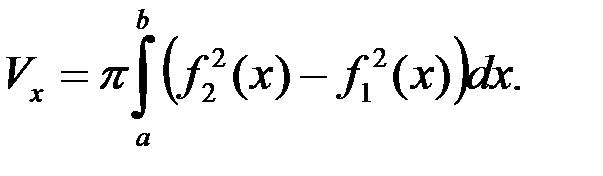
Определение 1. Поверхность вращения – это поверхность, которая получается при вращении плоской линии 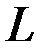 вокруг оси, лежащей в её плоскости и не пересекающей её.
вокруг оси, лежащей в её плоскости и не пересекающей её.
Ось вращения может и пересекать линию, если это ось симметрии линии. В этом случае рассматривают лишь «половину» линии.
Впишем в кривую 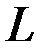 произвольную ломанную и обозначим
произвольную ломанную и обозначим 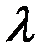 длину наибольшего её звена. При вращении этой ломанной вокруг оси мы получим поверхность
длину наибольшего её звена. При вращении этой ломанной вокруг оси мы получим поверхность 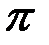 , составленную из боковых поверхностей усеченных конусов. Обозначим площадь этой поверхности
, составленную из боковых поверхностей усеченных конусов. Обозначим площадь этой поверхности 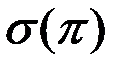 .
.
Определение 2. Конечный предел 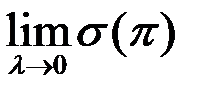 называют площадью поверхности вращения.
называют площадью поверхности вращения.
Можно показать, что если линия 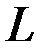 имеет длину, то поверхность, полученная её вращением, имеет площадь.
имеет длину, то поверхность, полученная её вращением, имеет площадь.
II Общая формула
Линия 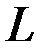 , вращением которой вокруг оси абсцисс получена поверхность, может быть задана одним из следующих способов:
, вращением которой вокруг оси абсцисс получена поверхность, может быть задана одним из следующих способов:
1) 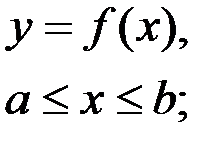 2)
2) 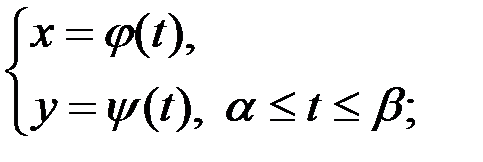 3)
3) 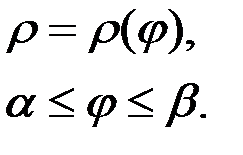
Теорема. Если функции, определяющие линию, непрерывны вместе со своими производными, то площадь поверхности вращения (вокруг оси 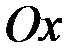 ) определяется формулой:
) определяется формулой:
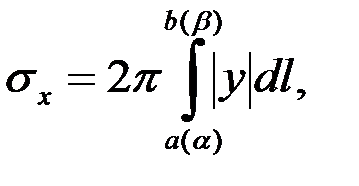 (1)
(1)
где 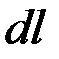 – подынтегральное выражение, фигурирующее в соответствующей формуле для длины дуги.
– подынтегральное выражение, фигурирующее в соответствующей формуле для длины дуги.
Идея доказательства. Пусть концы 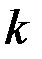 -го звена ломанной имеют координаты
-го звена ломанной имеют координаты 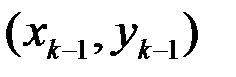 и
и 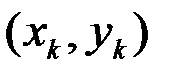 . Это звено при вращении вокруг оси
. Это звено при вращении вокруг оси 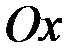 опишет боковую поверхность усеченного конуса с радиусами оснований
опишет боковую поверхность усеченного конуса с радиусами оснований 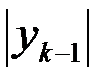 и
и 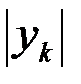 и образующей
и образующей 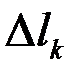 (длина
(длина 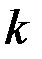 -го звена). Для площади такой поверхности известна формула
-го звена). Для площади такой поверхности известна формула
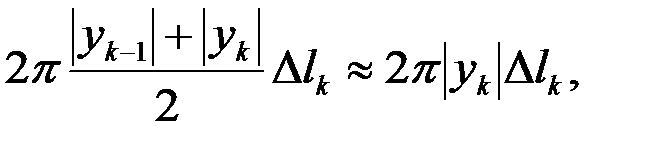
Вся ломанная даст поверхность с площадью
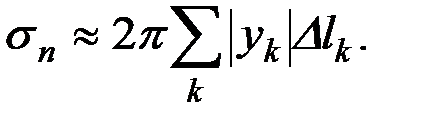
Если, например, имеющаяся кривая – это график функции 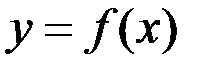 , тогда
, тогда 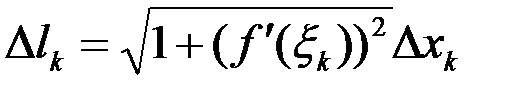 (см. §3, II). Также, заменяя
(см. §3, II). Также, заменяя 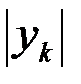 на
на 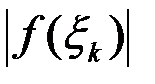 получим
получим
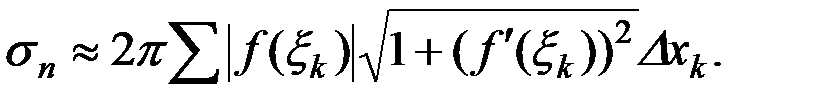
В этой сумме нетрудно увидеть интегральную сумму, которая в пределе даст интеграл из (1).
21. Спрямляемые дуги. Достаточное условие справляемости дуг, вывод формулы для исчисления ее длины
. В приложениях математики возникает потребность в вычислении длин дуг произвольных кривых. Но, чтобы вычислить длину произвольной кривой, надо быть уверенным в том, что рассматриваемая кривая имеет конечную длину.
В средней школе длиной окружности называют предел последовательности периметров вписанных в окружность правильных многоугольников ( при неограниченном удвоении числа сторон). Однако это определение неприменимо к произвольным кривым.
Дадим общее определение понятия длины кривой. Пусть задана жорданова кривая Г1:
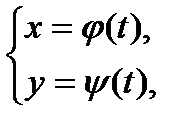 (1)
(1)
a 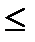 t
t 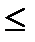 в.
в.
Напомним, что функции 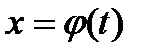 и
и 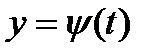 непрерывны на отрезке. Разобьём отрезок [а;в] на части числами
непрерывны на отрезке. Разобьём отрезок [а;в] на части числами
t0, t1,…, tn: a = t0 < t1 < … < tn = в.
Каждому числу t соответствует точка Мк ( 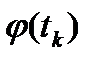 ,
, 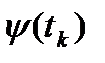 ) кривой Г. Проводя отрезки М0М1, …, Mn-1Mn, получим ломаную линию ɣ, вписанную в кривую Г. Обозначим её длину через l(ɣ).
) кривой Г. Проводя отрезки М0М1, …, Mn-1Mn, получим ломаную линию ɣ, вписанную в кривую Г. Обозначим её длину через l(ɣ).
Определение. Жорданова кривая (1) называется спрямляемой (имеющей длину), если множество 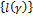 длин вписанных в эту кривую ломаных γ ограничено сверху. Точная верхняя граница множества
длин вписанных в эту кривую ломаных γ ограничено сверху. Точная верхняя граница множества 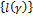 называется длиной кривой Γ и обозначается
называется длиной кривой Γ и обозначается 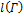 :
:
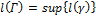 . (2)
. (2)
Докажем, что длина спрямляемой кривой обладает свойством аддитивности.
Пусть жорданова кривая Γ разбита на кривые 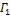 и
и 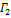 . Если эти кривые спрямляемы, то кривая Γ спрямляема, причем
. Если эти кривые спрямляемы, то кривая Γ спрямляема, причем 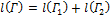 .
.
В самом деле, пусть γ – любая ломаная, вписанная в кривую Γ, и пусть М – точка, разбивающая Γ на 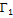 и
и 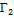 . Добавляя эту точку к вершинам ломаной γ, получим ломаную
. Добавляя эту точку к вершинам ломаной γ, получим ломаную 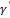 , длина которой не меньше длины ломаной γ,
, длина которой не меньше длины ломаной γ, 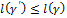 . Но ломаная
. Но ломаная 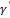 состоит из двух частей
состоит из двух частей 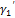 и
и 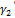 , вписанных соответственно в кривые
, вписанных соответственно в кривые 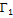 и
и 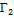 , причем
, причем 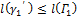 и
и 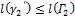 .
.
Поэтому
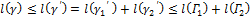 .
.
Это неравенство показывает, что число 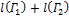 является одной из верхних границ для множества
является одной из верхних границ для множества 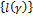 длин ломаных, вписанных в кривую Γ. Но для любого
длин ломаных, вписанных в кривую Γ. Но для любого 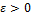 найдутся ломаные
найдутся ломаные 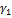 и
и 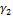 , вписанные в
, вписанные в 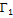 и
и 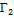 , такие, что
, такие, что
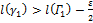 и
и 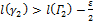 .
.
Объединяя 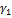 и
и 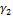 , получаем ломаную γ, вписанную в Γ и такую, что
, получаем ломаную γ, вписанную в Γ и такую, что
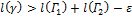 .
.
А это и значит, что 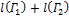 - точная верхняя граница множества
- точная верхняя граница множества 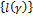 , т.е.
, т.е.
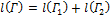 .
.
А) Несобственные интегралы с бесконечными пределами интегрирования
Первая теорема сравнения. Пусть 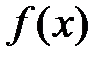 и
и 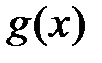 определены на
определены на 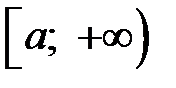 , интегрируемы на любом отрезке
, интегрируемы на любом отрезке 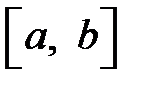 , где
, где 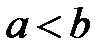 и
и 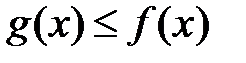 , причем
, причем 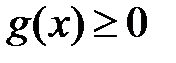 . Тогда:
. Тогда:
1. если сходится 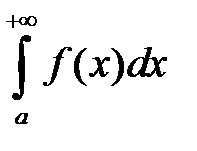 , то сходится и
, то сходится и 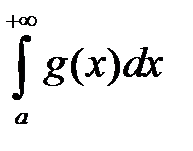 ;
;
2. если расходится 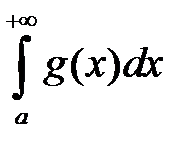 , то расходится и
, то расходится и 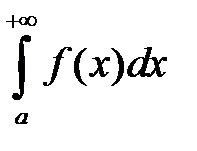 .
.
Вторая теорема сравнения.Пусть функции 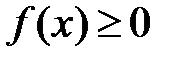 и
и 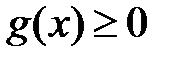 определены на
определены на 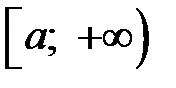 , и пусть существует
, и пусть существует 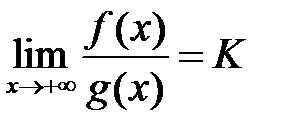 . Тогда
. Тогда
1) Если 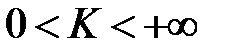 , то
, то 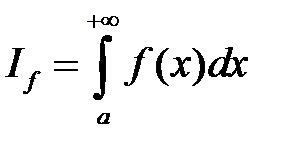 и
и 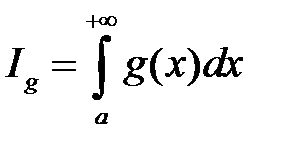 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
2) Если 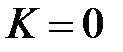 , то из сходимости
, то из сходимости 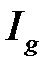 следует сходимость
следует сходимость 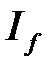 , а из расходимости
, а из расходимости 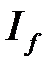 следует расходимость
следует расходимость 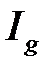 .
.
3) Если 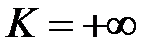 , то из сходимости
, то из сходимости 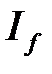 следует сходимость
следует сходимость 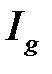 , а из расходимости
, а из расходимости 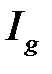 следует расходимость
следует расходимость 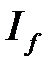 .
.
Б) Несобственные интегралы от неограниченных функций.
Первая теорема сравнения. Пусть на отрезке 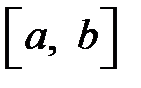 функции
функции 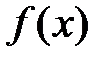 и
и 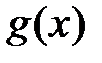 разрывны в точке
разрывны в точке 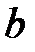 , и для каждого
, и для каждого 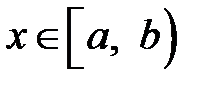 выполняется неравенство
выполняется неравенство 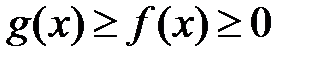 . Тогда если сходится
. Тогда если сходится 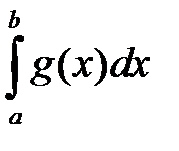 , то сходится и
, то сходится и 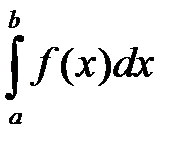 ; если расходится
; если расходится 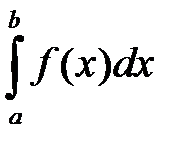 , то расходится и
, то расходится и 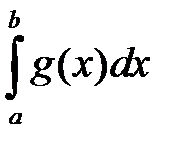 .
.
Вторая теорема сравнения.Пусть на отрезке 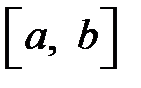 функции
функции 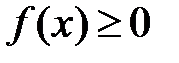 и
и 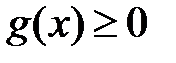 разрывны в точке
разрывны в точке 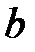 , и пусть существует
, и пусть существует 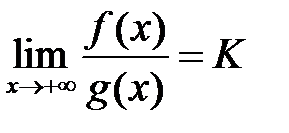 . Тогда:
. Тогда:
1) Если 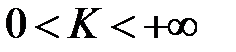 , то
, то 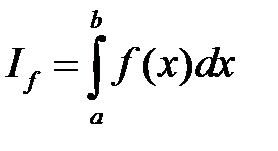 и
и 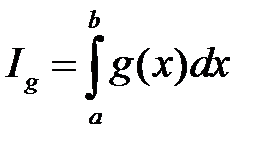 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
2) Если 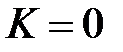 , то из сходимости
, то из сходимости 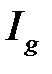 следует сходимость
следует сходимость 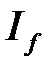 , а из расходимости
, а из расходимости 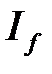 следует расходимость
следует расходимость 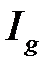 .
.
3) Если 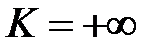 , то из сходимости
, то из сходимости 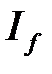 следует сходимость
следует сходимость 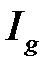 , а из расходимости
, а из расходимости 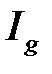 следует расходимость
следует расходимость 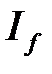 .
.
25. Собственные интегралы зависящие от параметра, их непрерывности и дифференцируемости.
Для того чтобы дать определение интеграла, зависящего от параметра, введем функцию 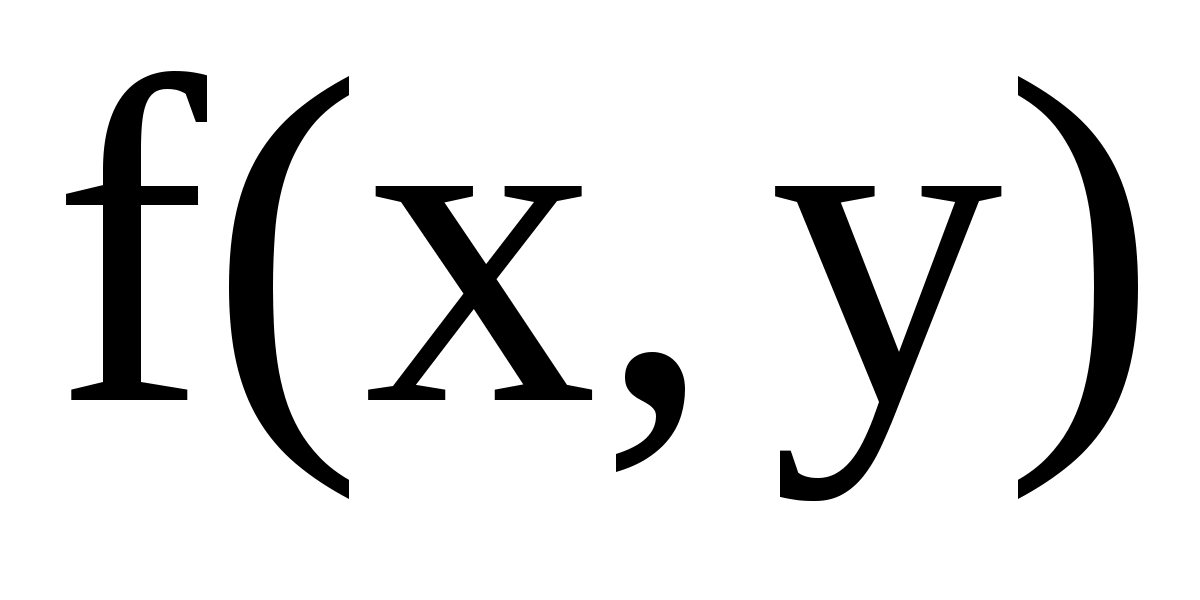 . Пусть эта функция
. Пусть эта функция 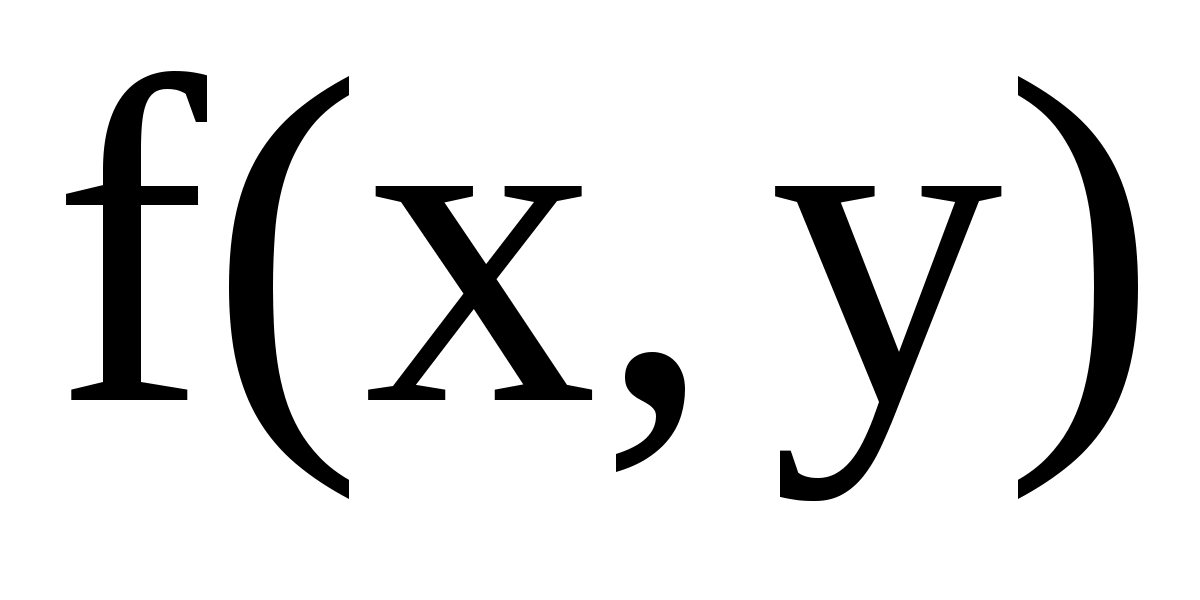 будет определена на некотором множестве, где
будет определена на некотором множестве, где 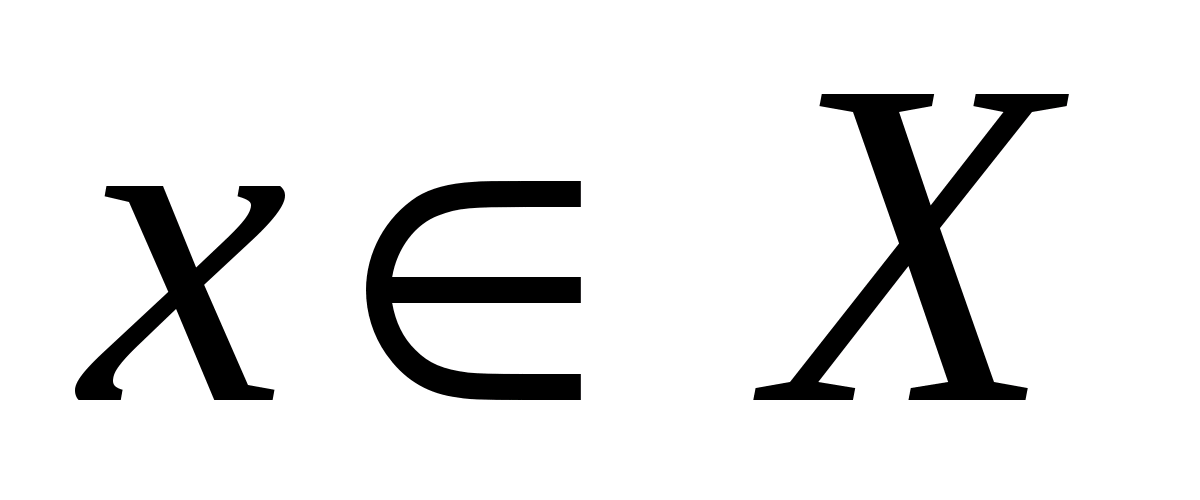 и
и 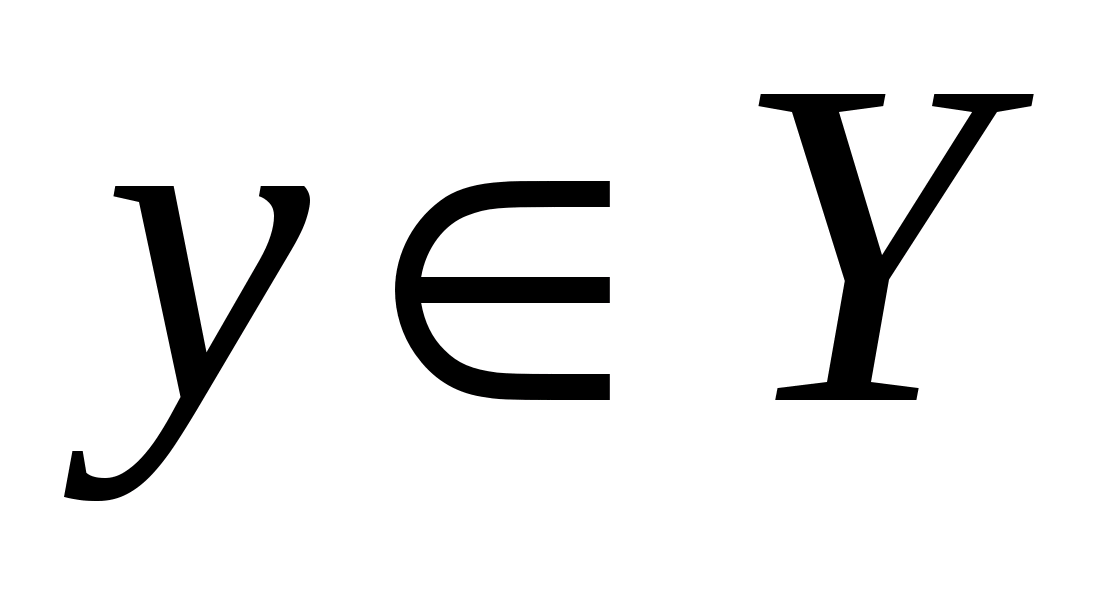 , то есть в результате получится множество
, то есть в результате получится множество 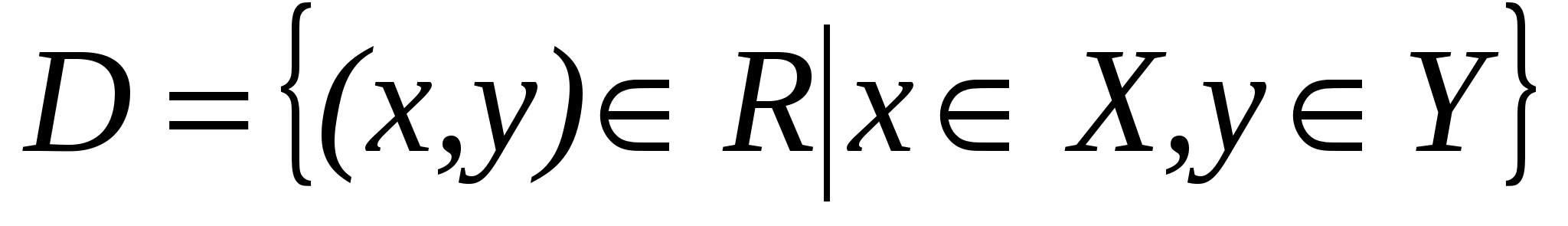 . Если функция
. Если функция 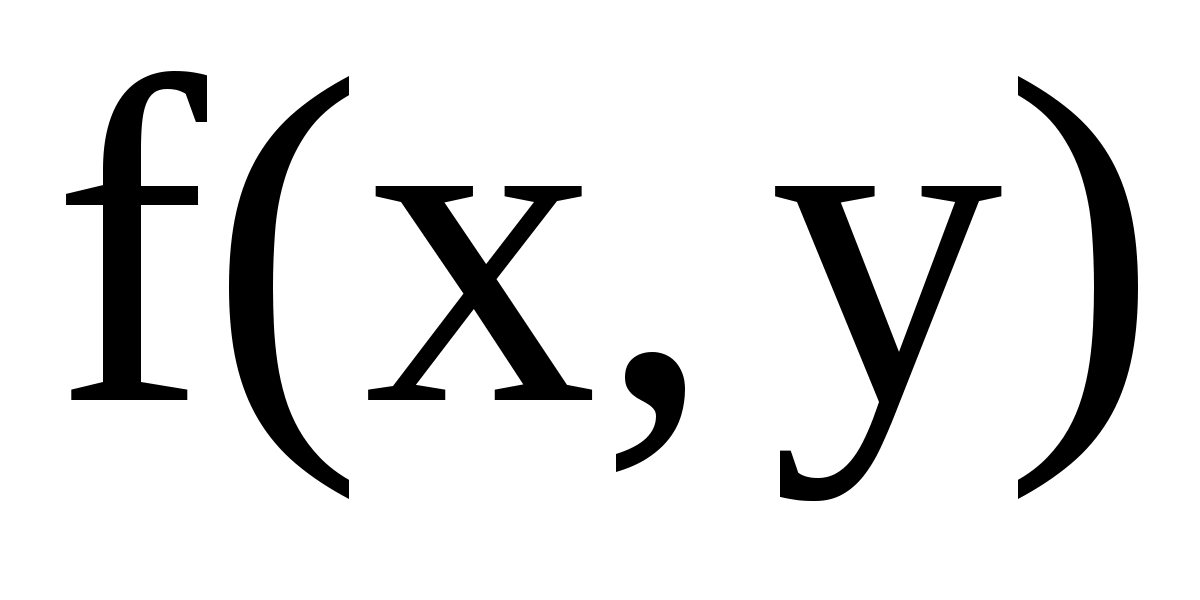 непрерывна в D, то тогда имеет смысл интеграл
непрерывна в D, то тогда имеет смысл интеграл 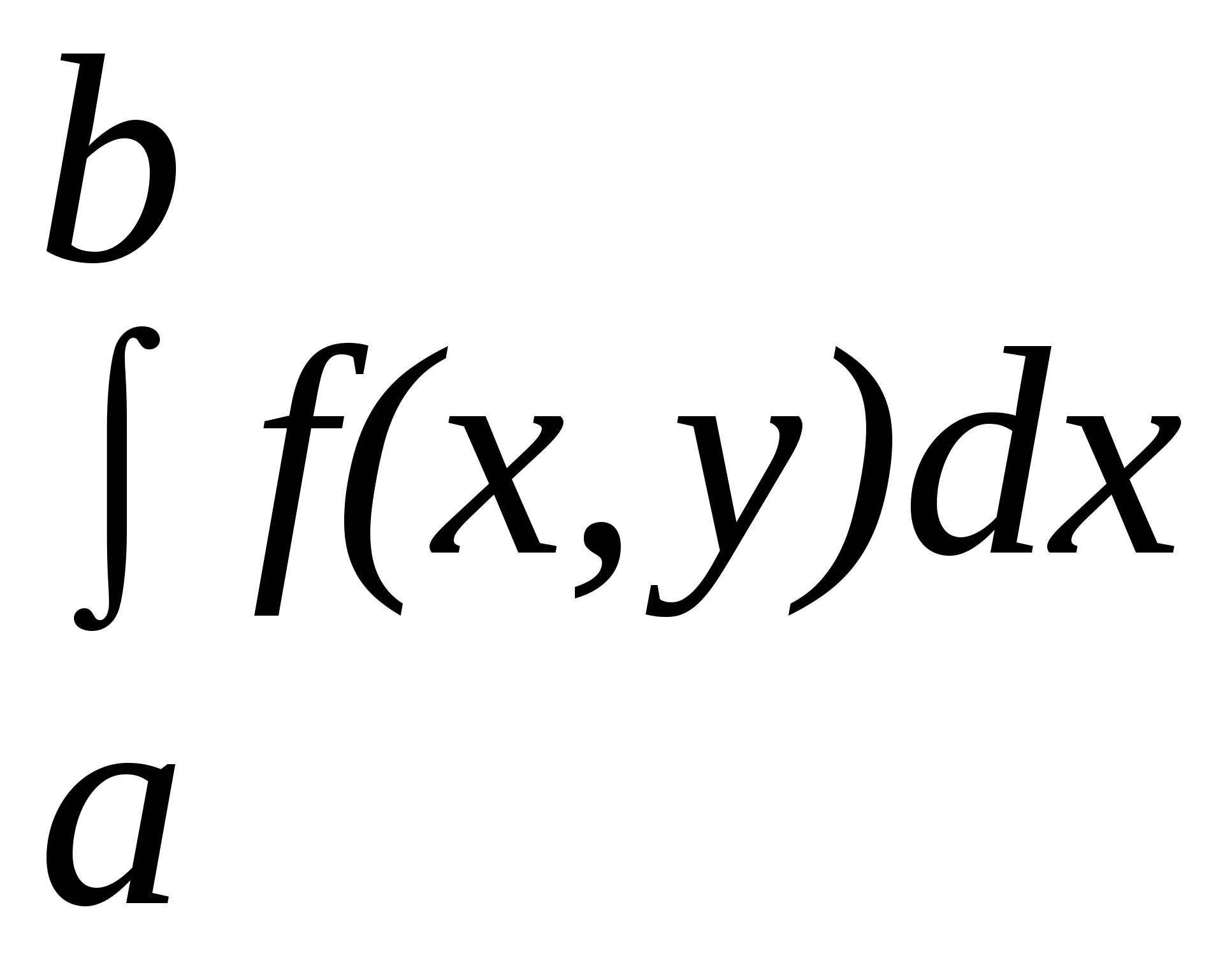 , где x принадлежит некоторому конечному или бесконечному промежутку
, где x принадлежит некоторому конечному или бесконечному промежутку 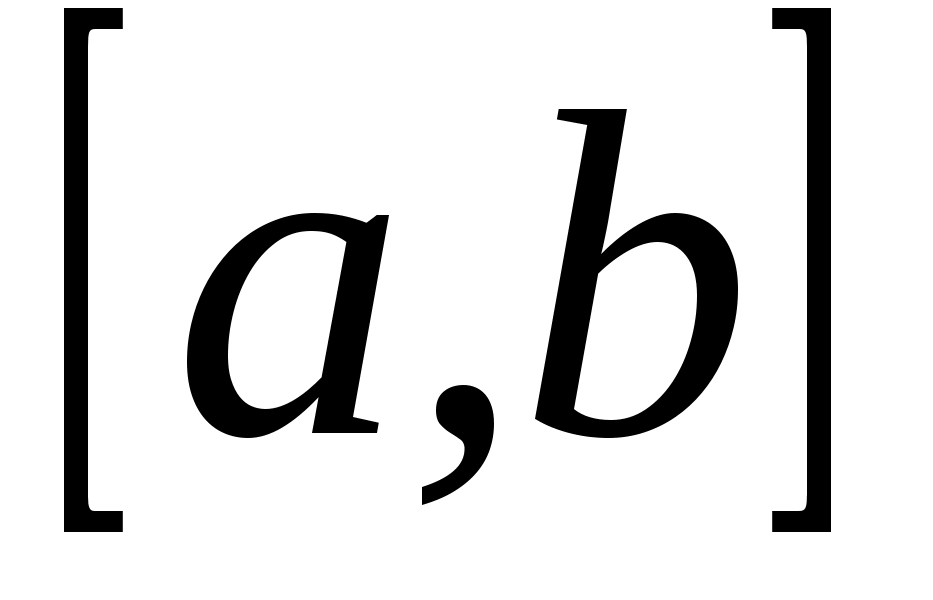 , значит, интеграл может быть несобственным.
, значит, интеграл может быть несобственным.
На основании этого можно дать определение интеграла, зависящего от параметра.
Определение.
Интеграл 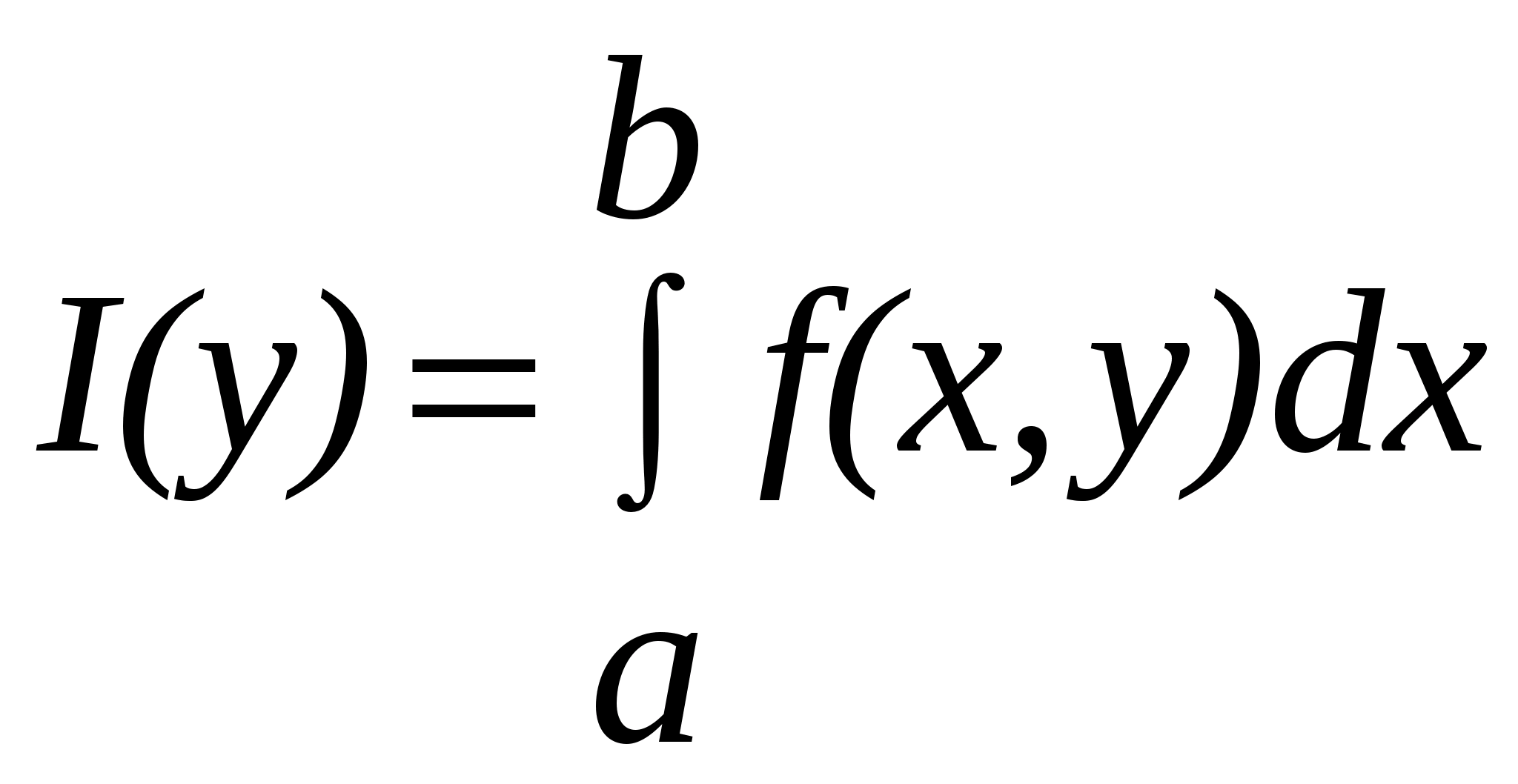 называется интегралом, зависящим от параметра, если
называется интегралом, зависящим от параметра, если 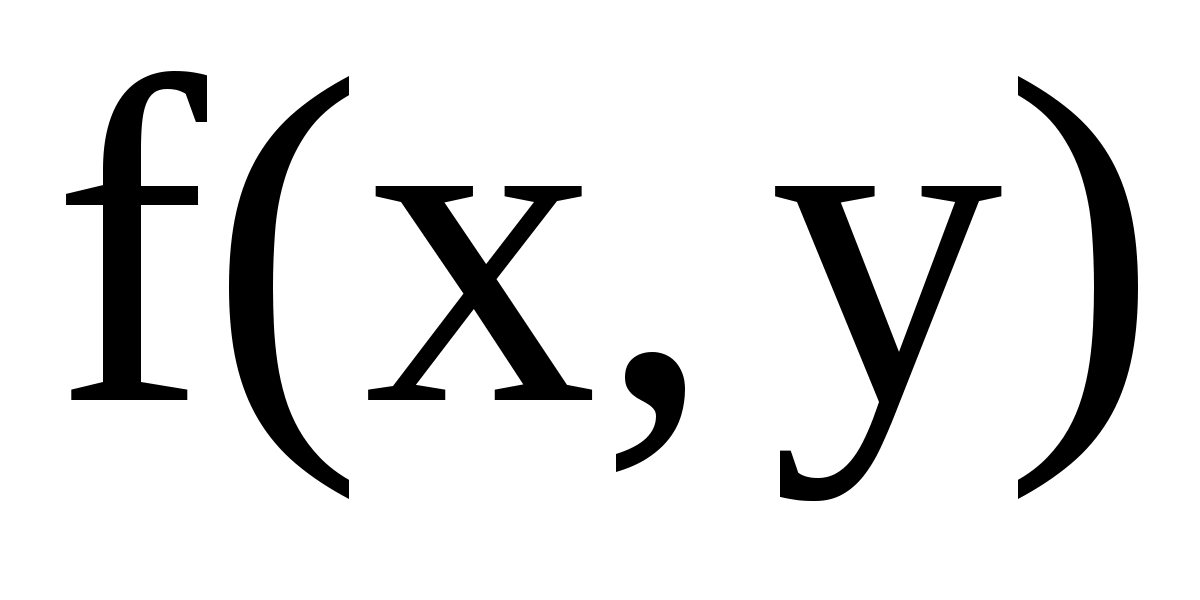 интегрируема на промежутке
интегрируема на промежутке 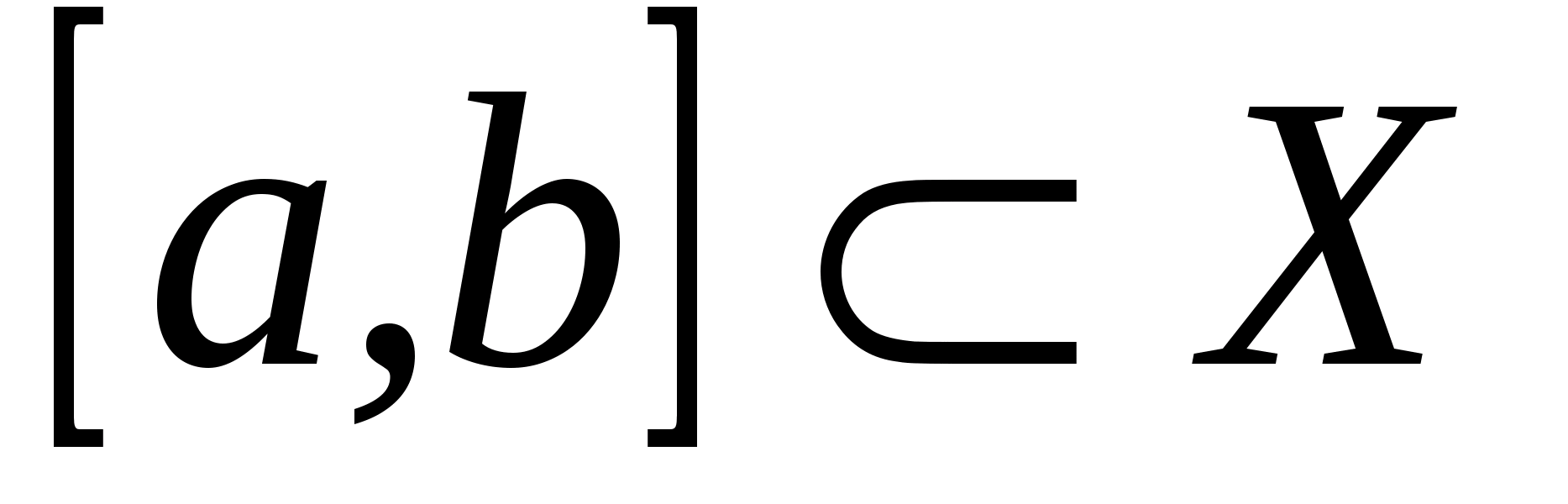 при любом фиксированным
при любом фиксированным 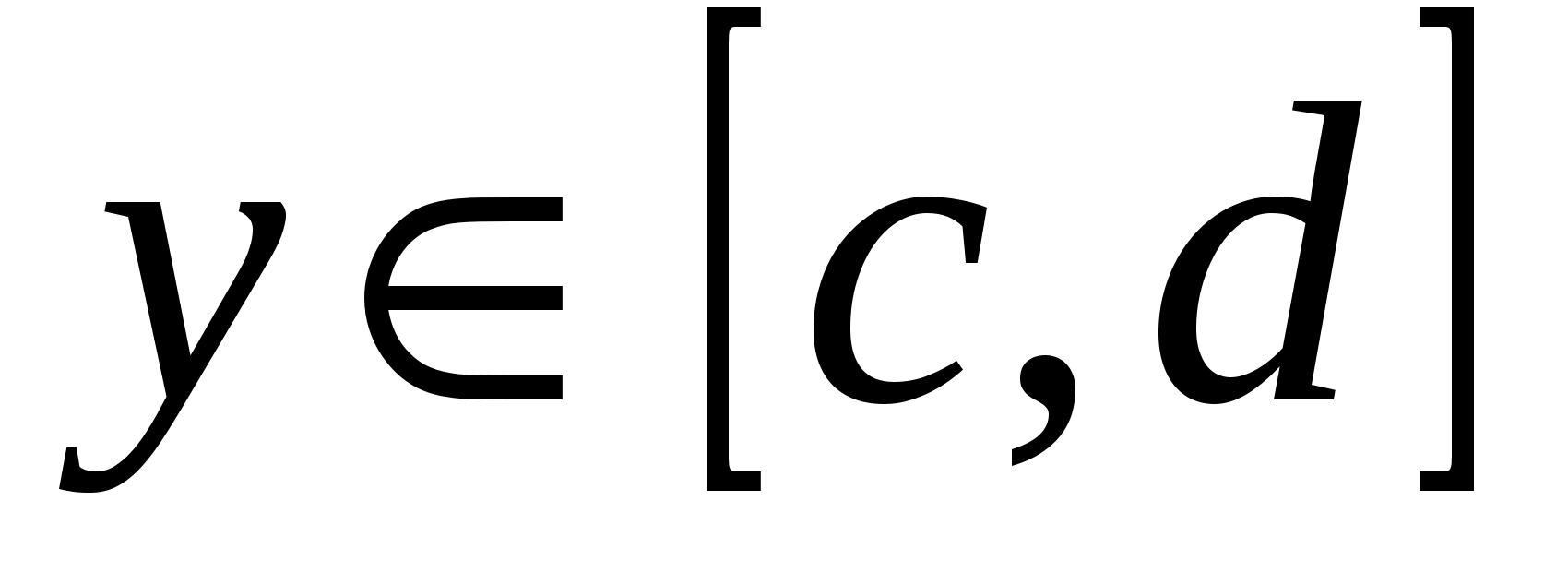 , где .
, где .
Следовательно, представляет собой функцию 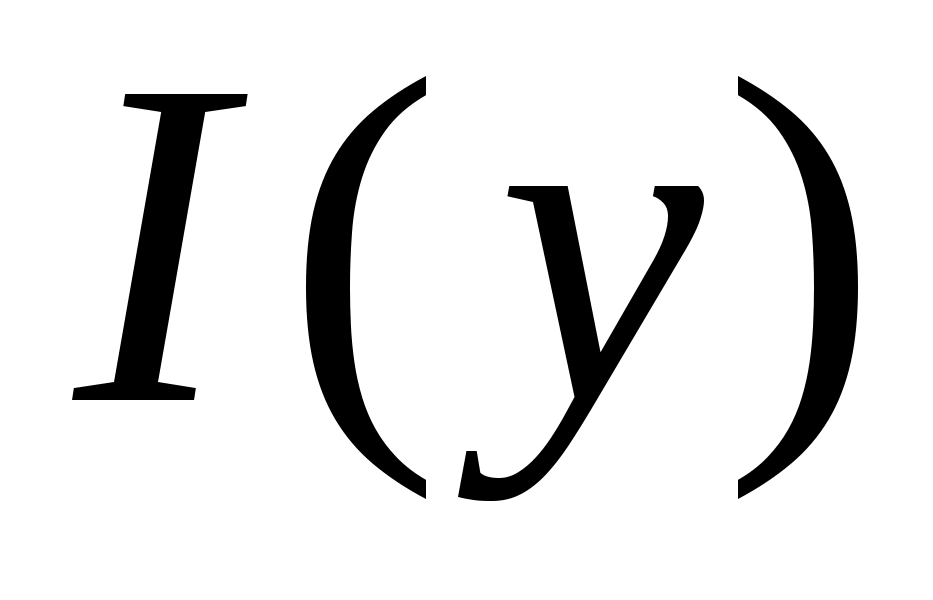 переменной (параметра)
переменной (параметра) 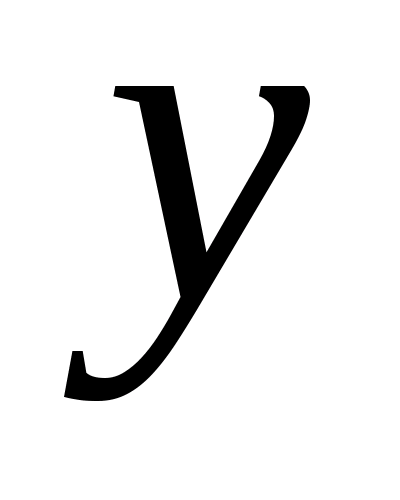 , определенную в промежутке
, определенную в промежутке 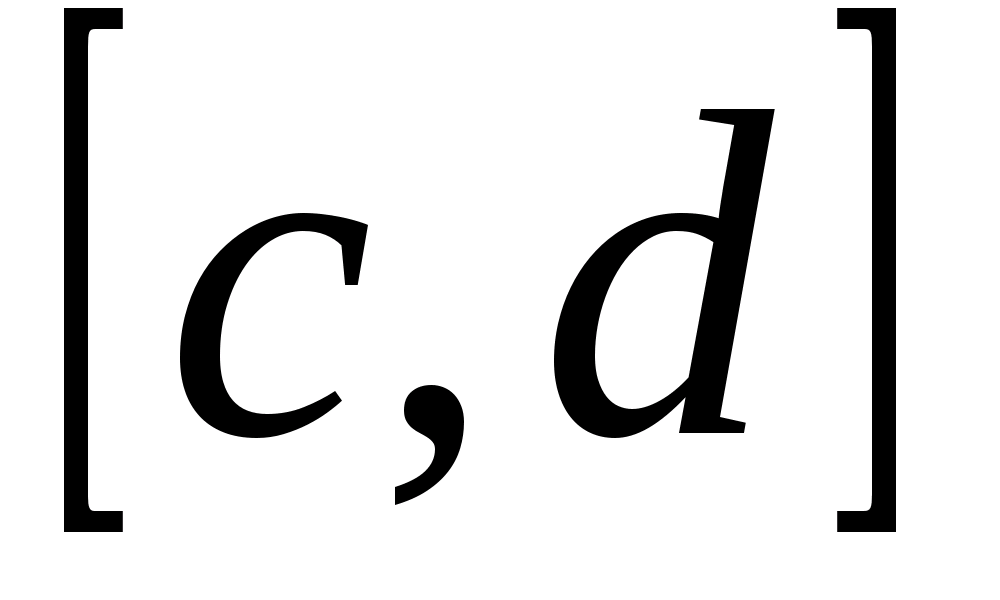 . Возможно также существование интеграла при фиксированном
. Возможно также существование интеграла при фиксированном 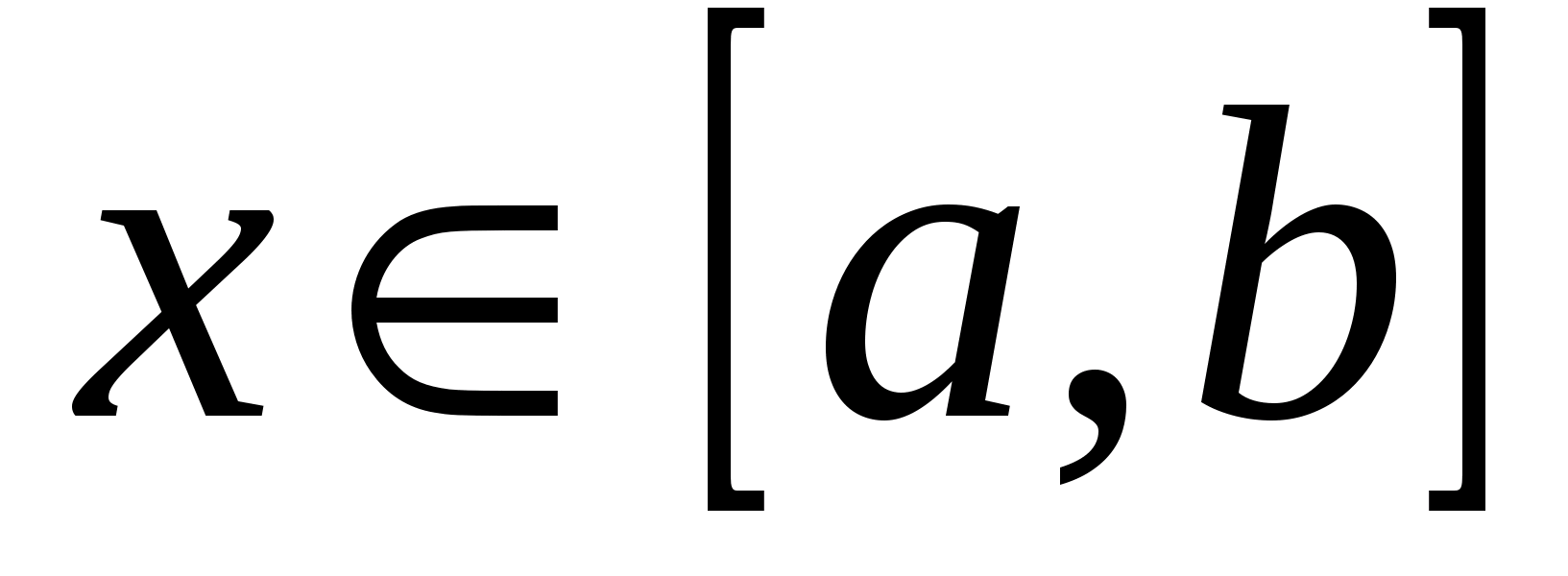 , тогда он будет представлять собой функцию переменной (параметра)
, тогда он будет представлять собой функцию переменной (параметра) 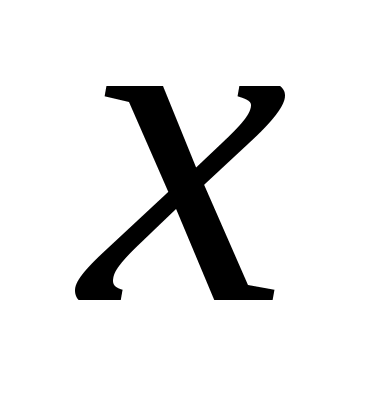 , определенную в промежутке
, определенную в промежутке 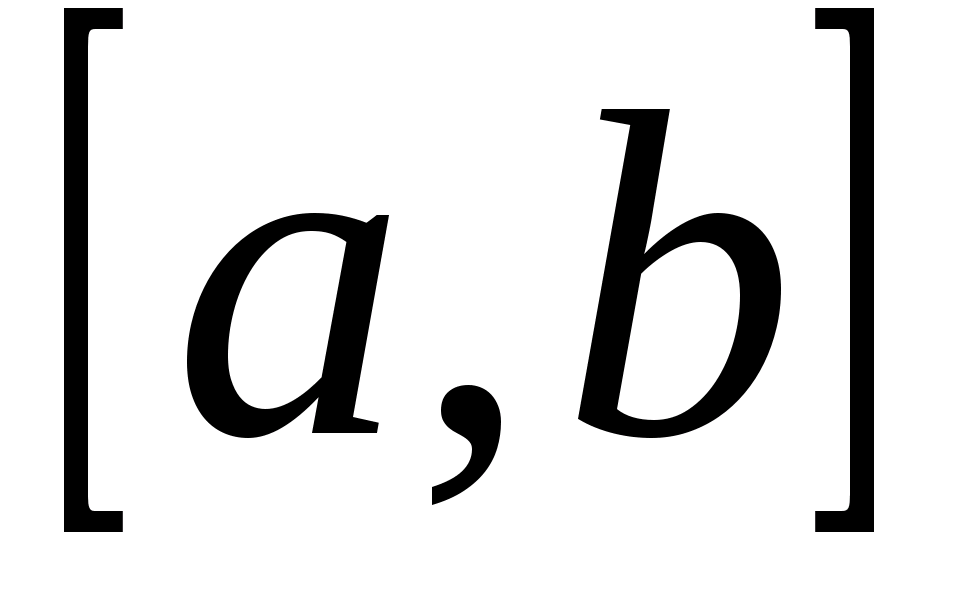 . Обозначается она так
. Обозначается она так 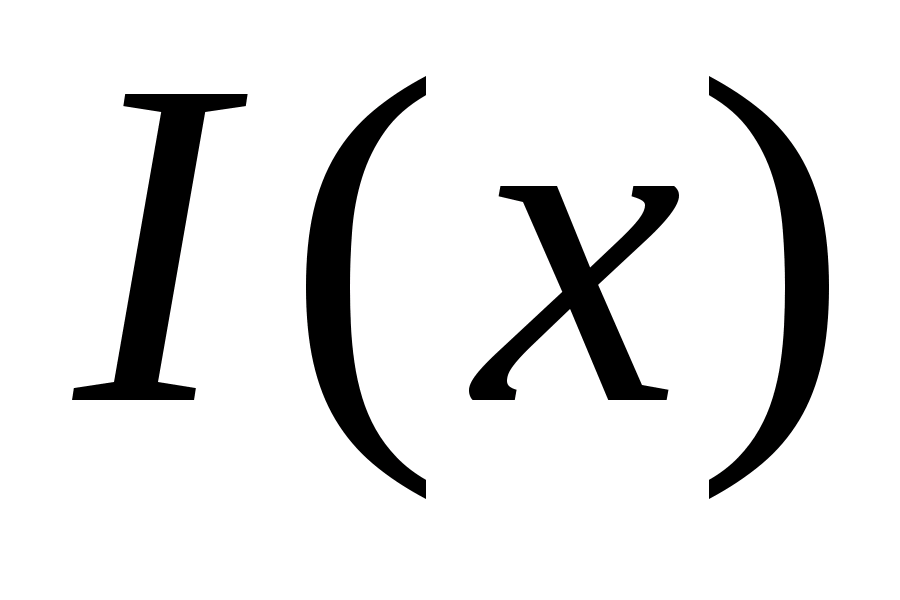 , так что
, так что 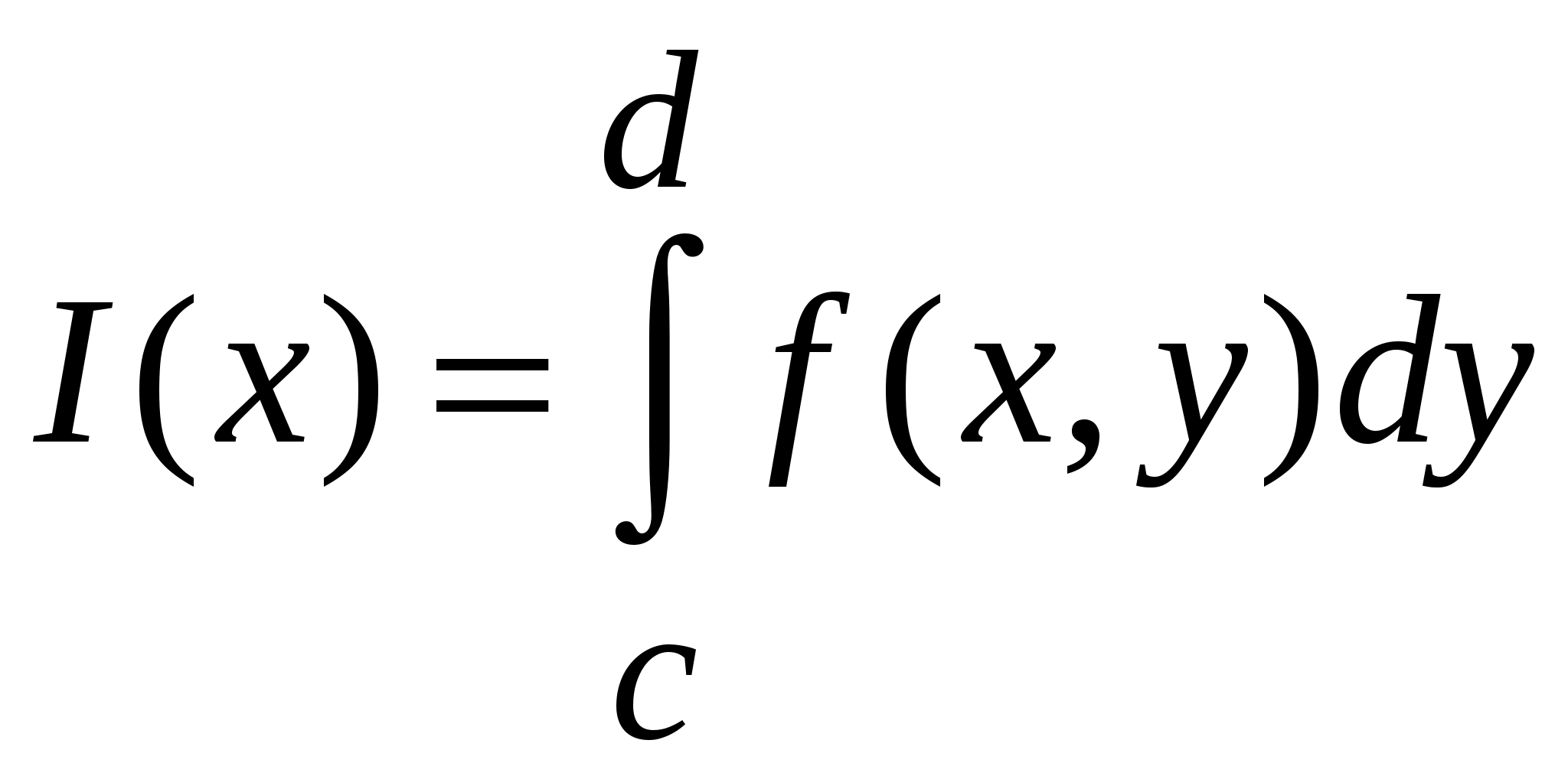 .
.
Основная задача будет состоять в том, чтобы, зная свойства функции 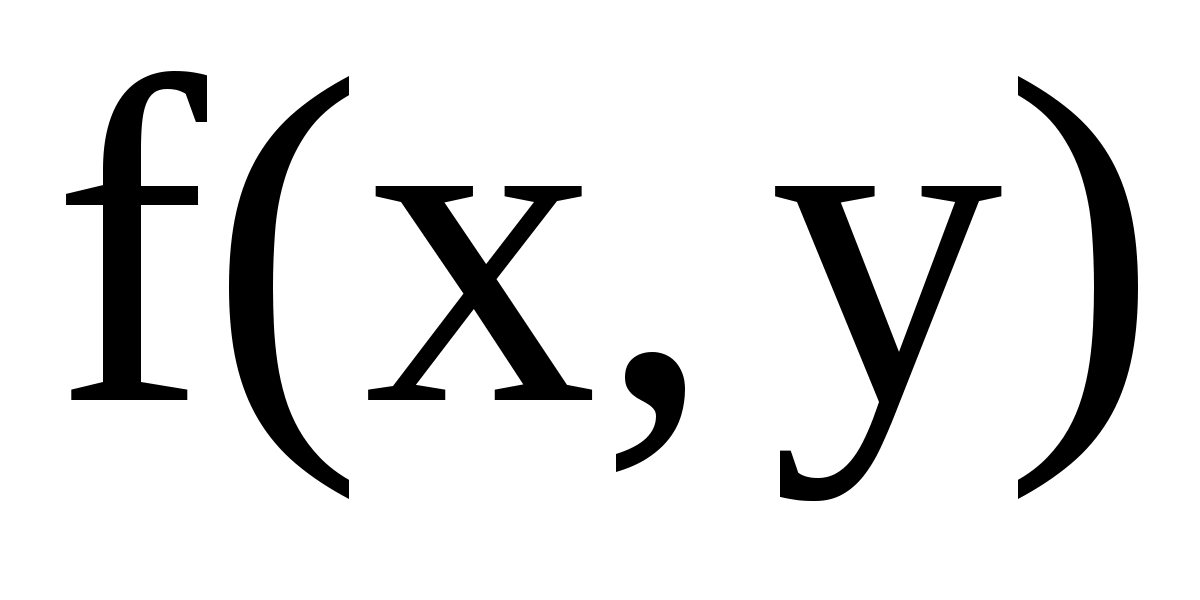 , получить информацию о свойствах функции
, получить информацию о свойствах функции 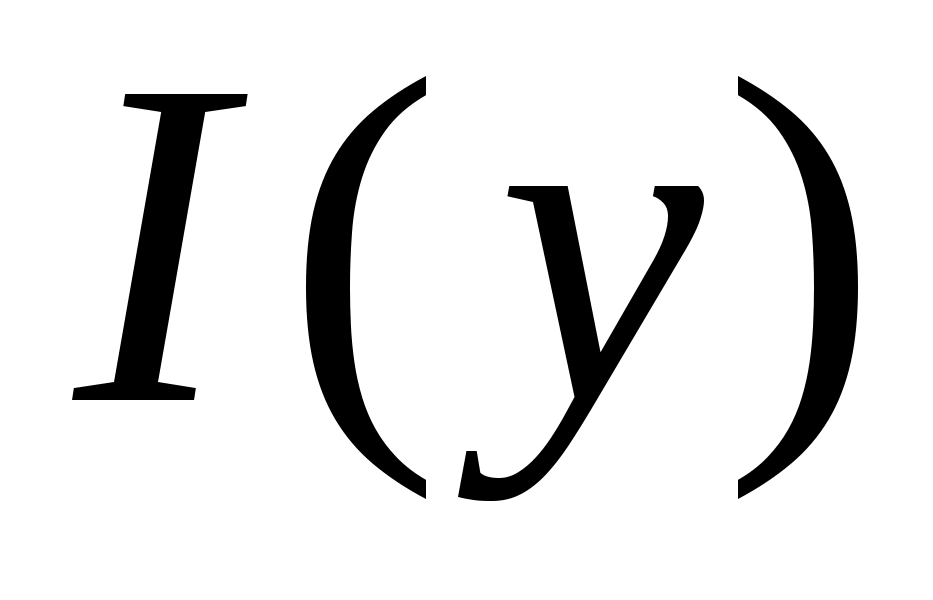 . Эти свойства имеют многообразные применения, особенно при вычислении несобственных интегралов.
. Эти свойства имеют многообразные применения, особенно при вычислении несобственных интегралов.
Пример. Найти интеграл 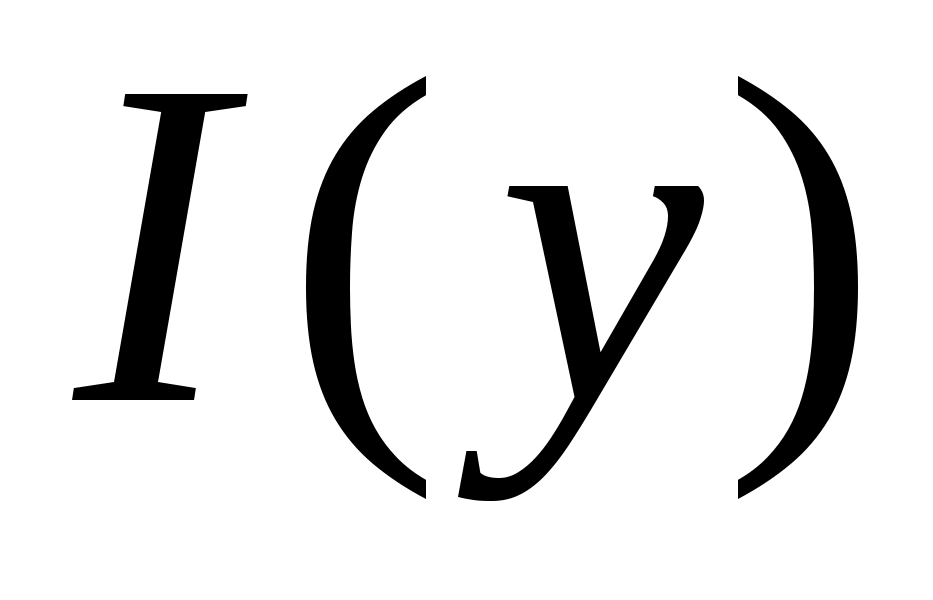 от функции
от функции 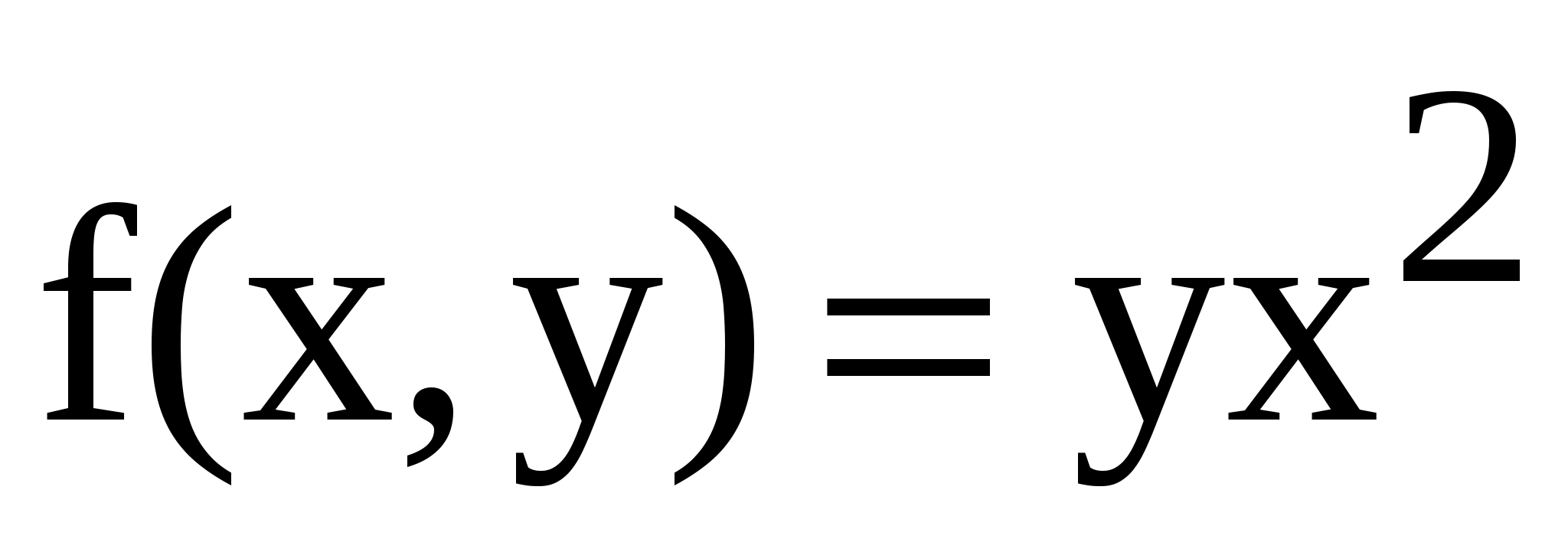 ,
, 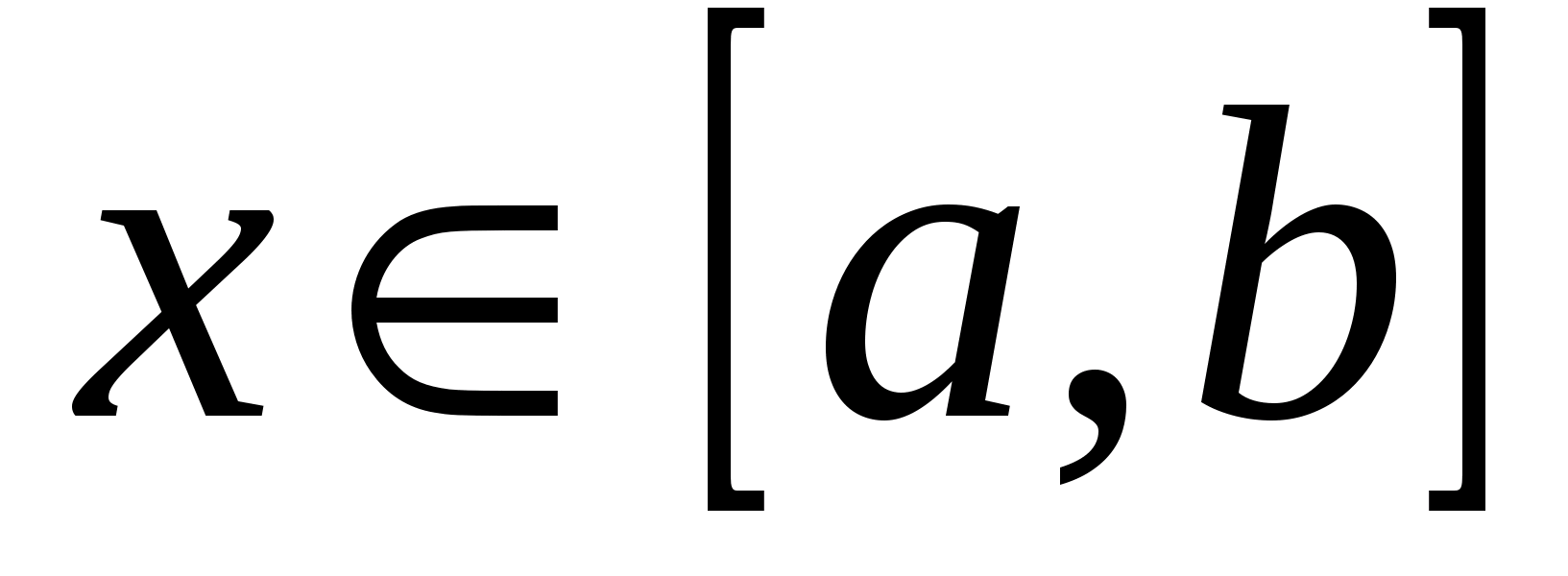
Функция 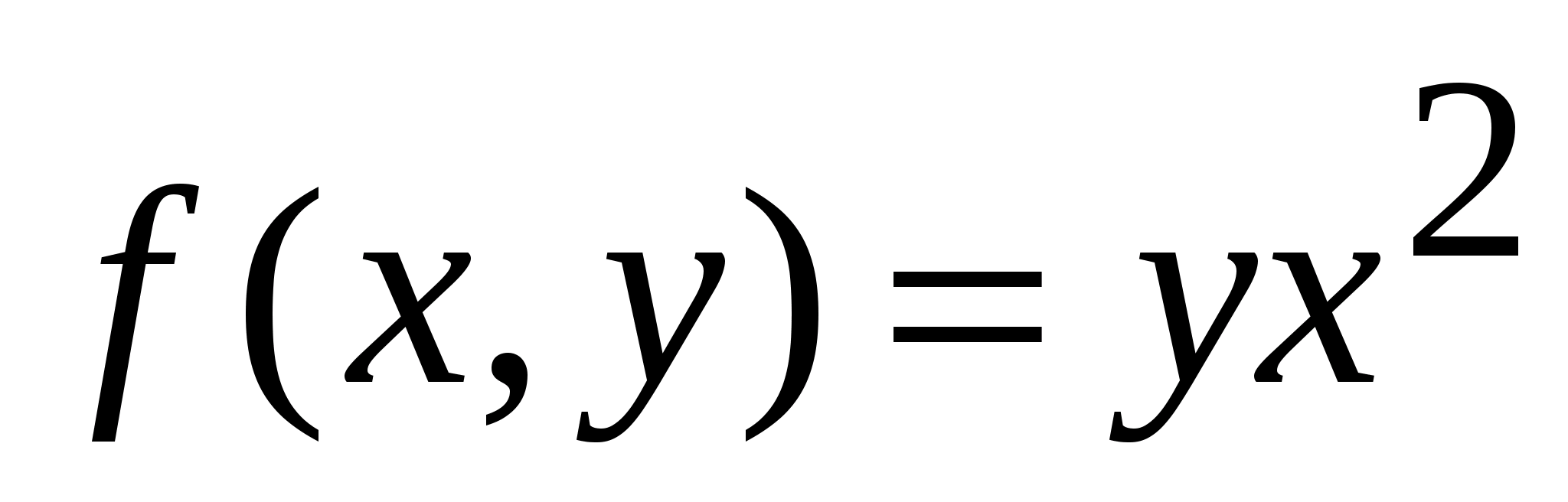 непрерывна на отрезке
непрерывна на отрезке 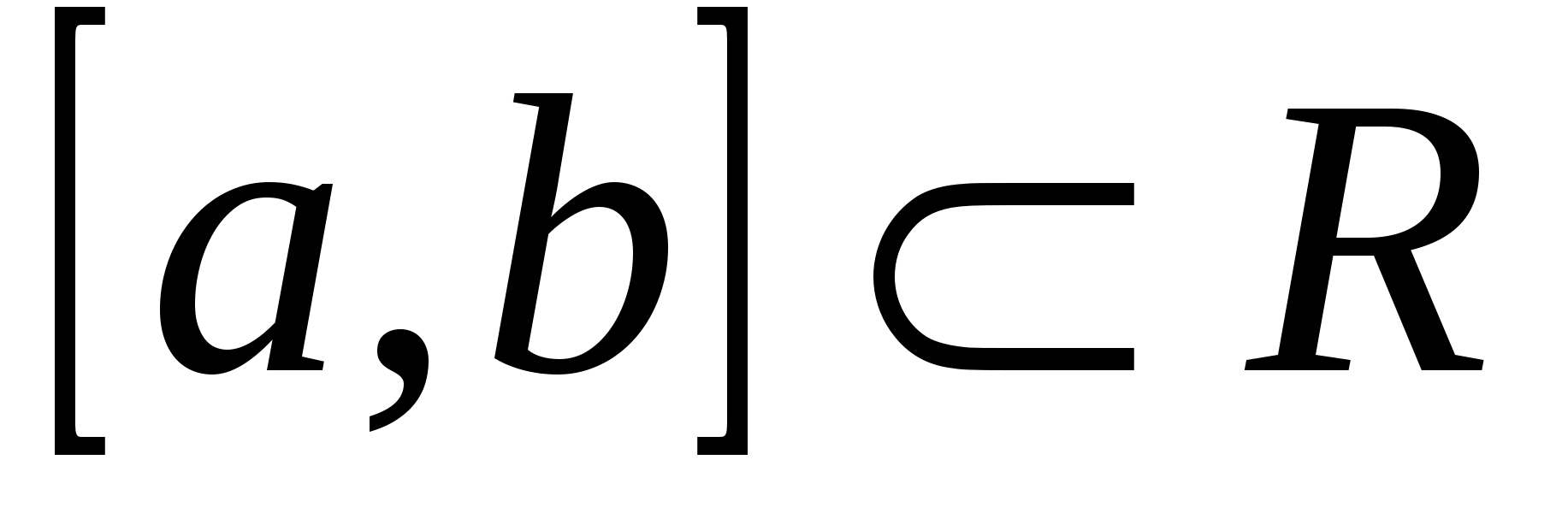 при любом фиксированном
при любом фиксированном 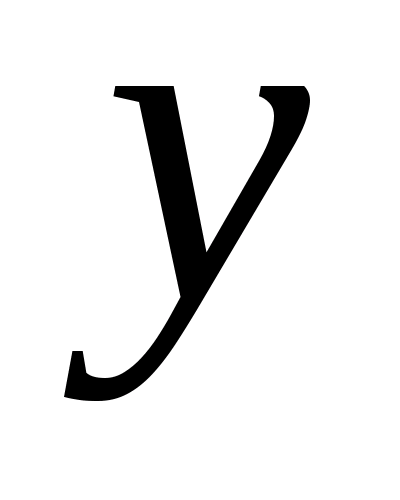 , а значит, она интегрируема. Тогда
, а значит, она интегрируема. Тогда
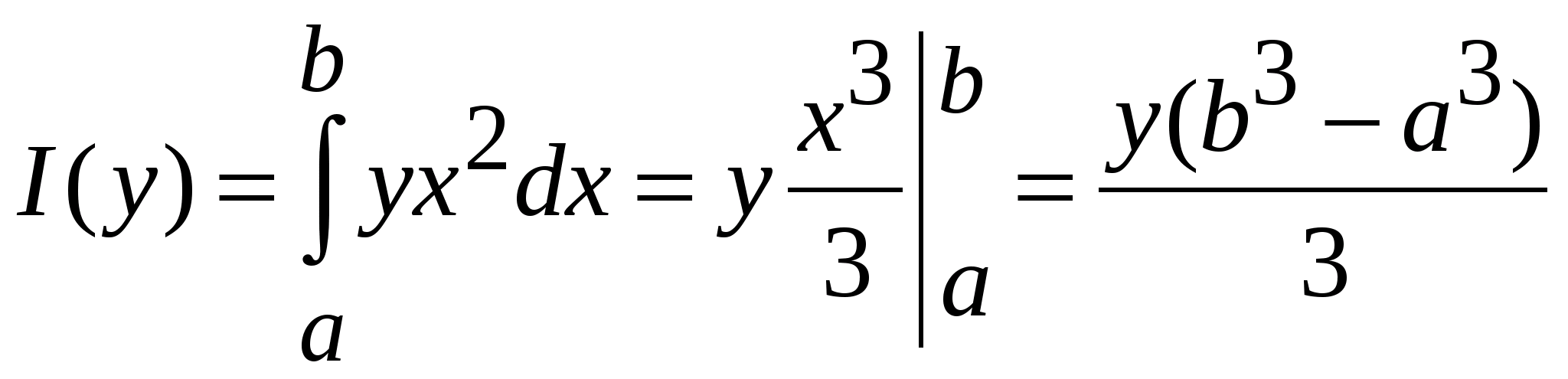 .
.
Масса тела.
Масса тела при заданной объемной плотности μ вычисляется с помощью тройного интеграла 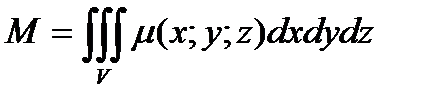 .
.
Статические моменты.
Моменты 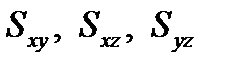 тела относительно координатных плоскостей Oxy, Oxz, Oyz вычисляются по формулам
тела относительно координатных плоскостей Oxy, Oxz, Oyz вычисляются по формулам
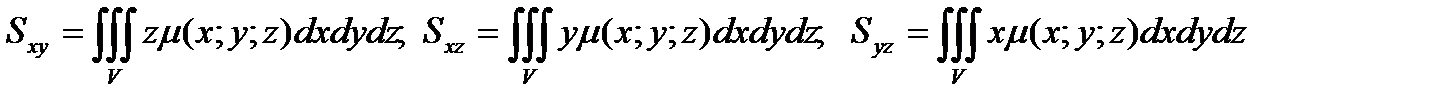 .
.
Центр тяжести тела.
Координаты центра тяжести тела V находятся по формулам
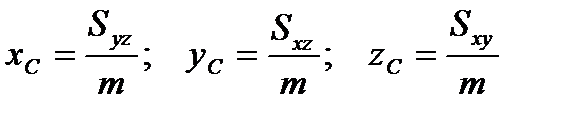 .
.
32 Вычисление криволинейных и поверхностных интегралов 1-го рода
Рассмотрим на плоскости или в пространстве кривую L и функцию f, определенную в каждой точке этой кривой. Разобьем кривую на части Δsi длиной Δsi и выберем на каждой из частей точку Mi. Назовем d длину наибольшего отрезка кривой: 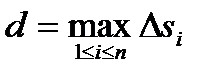 .
.
Криволинейным интегралом первого родаот функции f по кривой L называется предел интегральной суммы 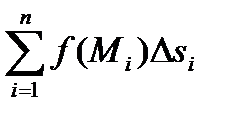 , не зависящий ни от способа разбиения кривой на отрезки, ни от выбора точек Mi:
, не зависящий ни от способа разбиения кривой на отрезки, ни от выбора точек Mi:
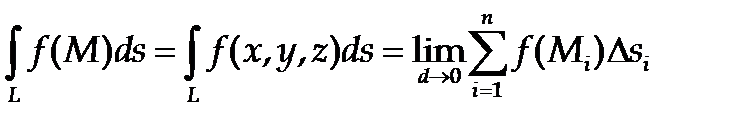 (24)
(24)
Если кривую
