Свойства чётности и нечётности.

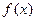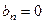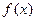Если чётная, то и ряд состоит только из константы и косинусов. При вычислении в интеграле одна функция чётная, а синус нечётный, произведение нечётное. Интеграл от нечётной функции по симметричному отрезку равен 0. Аналогично, если нечётная, то 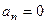, ведь в интеграле одна нечётная вторая чётная, и интеграл получается от нечётной, по симметричному промежутку, и он равен 0.

Ряд Фурье более подробно учитывает поведение функции на всём протяжении промежутка, в отличие от ряда Тейлора, который учитывает производные только в одной точке.

Пример. Разложить в тригонометрический ряд Фурье функцию на интервале (-1,1).

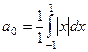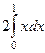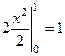= = , при этом 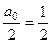, кстати, это и есть средняя высотра графика.

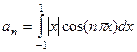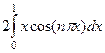= , интегрируем по частям.

, , .

= =

= = .

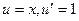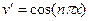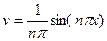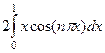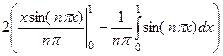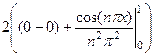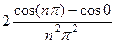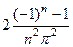Обратите внимание, что 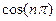равен 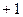при чётных n и 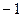при нечётных, поэтому совпадает с .

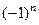Коэффициенты 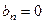так как функция чётная. Итак, получаем ряд:

.

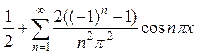Более подробная запись:

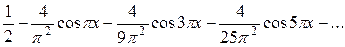
Графики:

Зелёным цветом показан график модуля,

красным частичная сумма .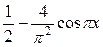

синим - частичная сумма .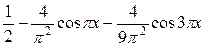

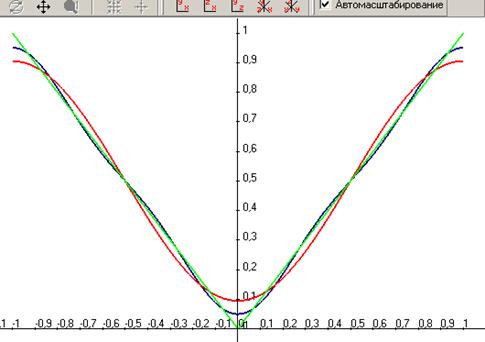
Периодическое продолжение.

Мы ищем разложение функции в ряд на , однако функции sin и cos существуют на всей действительной оси. Таким образом, в каждой точке из интервала они принимают точно такое же значение, как и в точке . Таким образом, ряд Фурье сходится на к точно такой же функции, как и на . То же самое будет на , и на , и так далее. Получается, что сумма ряда Фурье это функция, определённая на всей числовой оси,

Поведение ряда в точках разрыва, теорема Дирихле.

Ряд Фурье в точке разрыва сходится к среднему арифметическому правостороннего и левостороннего пределов функции в этой точке: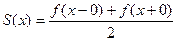

Если точка разрыва на конце интервала, то .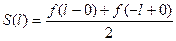

Гармонический вид ряда Фурье.

Обозначим 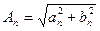тогда , .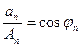

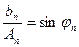Другими словами, если есть какие-то два числа 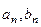, то можно создать такой прямоугольный треугольник, что катеты будут именно такие по величине. Тогда 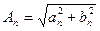- гипотенуза.

Угол в этом треугольнике обозначим через .

В общем-то, это то же самое, что пересчитать в полярных координатах, 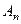и это аналог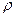и и 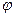, исходные 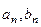аналоги 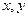. Тогда ряд принимает вид: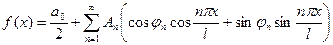

по тригонометрической формуле 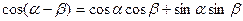можно свести к выражению:

здесь 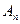- амплитуда, - частота, 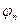- фаза.

Как видим, сумма 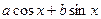на самом деле представляет собой одно колебание, одну волну, с амплитудой .

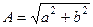Комплексный ряд Фурье.

Пусть комплексная функция действительного аргумента, то есть . Скалярное произведение комплекснозначных функций определено так: .

Вторая сопряжённая, т.к. только таким спосбом можно корректно ввести понятие нормы функции. Если по этому правилу умножать одну и ту же функцию, то = = . Таким образом, существует корень квадратный из этой величины, .

Рассмотрим систему функций т.е. причём при n = 0 получается именно , т.е. константа автоматически находится в составе такой системы функций.

Докажем ортогональность системы и вычислим квадраты нормвсех этих функций.

= = , что при означает

= так как на отрезке будет целое количество полных периодов этих тригонметрических функций.

Если вычислять это скалярное произведение при одном и том же номере n ,то мы получим этим самым квадраты норм этих функций.

= = = = = . Квадраты норм равны .

Комплексный ряд Фурье. .

Где , .

Пример. Найти комплексный ряд Фурье для функции:

. = = =

= = =

Ответ.

Кстати, если дальше преобразовать экспоненту в комплексной степени, то можно свести к обычному тригонометрическому ряду Фурье. Сделаем это. Объединим пары слагаемых при номерах .

=

=

=

.

ЛЕКЦИЯ № 15. 30.05.2017

Если записать подробнее комплексный ряд Фурье, т.е. внутри суммы подробно представить коэффициент, то получим:

.

Обозначим частоту . Приразение частоты от предыдущего к следующему номеру: .

Разложение в ряд Фурье существует для функции на для любого сколь угодно большого . При этом период увеличивается, а частота уменьшается. Если представить что то вся действительная ось представляет собой один большой период, при этом .

Очевидно, что можно рассматривать тригонометрические функции с любым действительным коэффициентом, т.е. может ьыть не лискретный, а непрерывный набор частот синуса и косинуса.

Предельным переходом при сумма превращается в интеграл (как интегральные суммы в прошлых темах).

Интеграл Фурье

Промежуточная переменная во внутренней части этого двойного интеграла пишется для того, чтобы отличать её от внешней переменной . Но ведь можно коэффициент поделить поровну между внешним и внутренним интегралом,

. Та функция от , которая здесь в скобке, называется преобразованием Фурье:

Преобразование Фурье

Когда мы не рассматриваем её в двойном интеграле, то можно не заменять на новую переменную .

Симметричность формул прямого и обратного преобразования Фурье:

и

Пример. Найти преобразование Фурье для функции

Решение. Здесь на левой части действительной оси функция тождественно 0, так что интеграл только по правой части: = =

. Можно ещё и домножить на сопряжённое, чтобы в знаменателе получить действительное выражение, тогда ответ: .