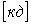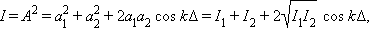При резонансе напряжений мощность источника тока будет затрачиваться только на преодоление активного сопротивления цепи, т. е. на нагрев проводников.
ТОК СМЕЩЕНИЯ. ОБОБЩЕННЫЙ ЗАКОН ПОЛНОГО ТОКА. УРАВНЕНИЕ МАКСВЕЛЛА. СЛЕДСТВИЕ ИЗ НИХ.
ТОК СМЕЩЕ́НИЯ, величина, пропорциональная скорости изменения переменного электрического поля в диэлектрике или вакууме. Название «ток» связано с тем, что ток смещения, так же как и ток проводимости, порождает магнитное поле.
При построении теории электромагнитного поля Дж. К. Максвелл выдвинул гипотезу о том, что магнитное поле создается не только движением зарядов (током проводимости, или просто током), но и любым изменением во времени электрического поля.
Понятие ток смещения введено Максвеллом для установления количественных соотношений между изменяющимся электрическим полем и вызываемым им магнитным полем.
В соответствии с теорией Максвелла, в цепи переменного тока, содержащей конденсатор, переменное электрическое поле в конденсаторе в каждый момент времени создает такое магнитное поле, какое создавал бы ток, (названный током смещения), если бы он протекал между обкладками конденсатора. Из этого определения следует, что Jсм= J (т. е., численные значения плотности тока проводимости и плотности тока смещения равны), и, следовательно, линии плотности тока проводимости внутри проводника непрерывно переходят в линии плотности тока смещения между обкладками конденсатора. Плотность тока смещения jсм характеризует скорость изменения электрической индукции D во времени:
Jсм = + dD/dt.
Ток смещения не выделяет джоулевой теплоты, его основное физическое свойство — способность создавать в окружающем пространстве магнитное поле.
ОБОБЩЕННЫЙ ЗАКОН ПОЛНОГО ТОКА
В общем случае магнитное поле определяется тремя токами: сторонним электрическим током Iэ током проводимости Iпр и током смещения. Если в процессе формирования магнитного поля участвуют все три тока, то закон полного тока следует записать в расширенной форме:

γэ – удельная электрическая проводимость среды
Е – напряженность электрического поля
Jэ – плотность электрического тока
Н – напряженность магнитного поля
УРАВНЕНИЯ МАКСВЕЛЛА
1. Электрическое поле может быть как потенциальным (EQ), так и вихревым (EB), поэтому напряженность суммарного поля E = EQ + EB.
Так как циркуляция вектора EQ равна нулю

а циркуляция вектора EB определяется выражением

то циркуляция вектора напряженности суммарного поля
 | [1] |
2. Обобщенная теорема о циркуляции вектора H

3. Теорема Гаусса для поля D

4. Теорема Гаусса для поля B

Величины, входящие в уравнения Максвелла, не являются независимыми и между ними существует следующая связь (изотропные несегнетоэлектрические и неферромагнитные среды):

где ε0 и μ0 – соответственно электрическая и магнитная постоянная, ε и μ – соответственно диэлектрическая и магнитная проницаемость, γ – удельная проводимость вещества.
Из уравнений Максвелла вытекает, что источниками электрического поля могут быть либо электрические заряды, либо изменяющиеся во времени магнитные поля, а магнитные поля могут возбуждаться либо движущимися электрическими зарядами (электрическими токами), либо переменными электрическими полями.
ВОЛНОВОЕ ДВИЖЕНИЕ. ПРОДОЛЬНЫЕ И ПОПЕРЕЧНЫЕ ВОЛНЫ. ФРОНТ ВОЛНЫ И ВОЛНОВАЯ ПОВЕРХНОСТЬ. ДЛИНА ВОЛНЫ. УРАВНЕНИЕ ПЛОСКОЙ ВОЛНЫ.
Волны - это изменение состояния среды (возмущения), распространяющиеся в этой среде и несущие с собой энергию и импульс без переноса вещества. Наиболее часто встречающиеся виды волн — упругие (звук) и электромагнитные (свет, радиоволны и другие).
Волновое уравнение: A = A0 cos(ωt + kx)
Волновое уравнение описывает распространение гармонических колебаний в пространстве. Характерными параметрами, описывающими гармоническую волну являются: A0 - амплитуда колебаний; ω - круговая частота (рад/с); период колебаний T (с), который связан с круговой частотой соотношением: T = 2π/ω; частота колебаний γ (Гц = 1/с) выражается через период: γ = 1/T; волновое число k = ω/v (где v- скорость распространения волны, измеряется в м/с); λ - длина (м) волны (λ = vT). Скорость распространения каждого вида волн зависит от свойств среды, в которой они распространяются.
Если взаимосвязь между частицами среды осуществляется силами упругости, возникающими вследствие деформации среды при передаче колебаний от одних частиц к другим, то волны называются продольными. К ним относятся звуковые, ультразвуковые, сейсмические и др. волны. Каждая частица колеблется по гармоническому закону в продольном направлении, совпадающем с направлением распространения волны. Амплитуда каждой частицы одинакова и равна A, а фаза колебаний линейно растёт с увеличением номера частицы на Dj т.е.
x0=Asin(wt); x1=Asin(wt+Dj); x2=Asin(wt+2Dj); x3=Asin(wt+3Dj); и т.д.
где w -частота волны, t - время, Dj - изменение фазы от частицы к частице
В поперечной волне колебания происходят в направлении, перпендикулярном направлению распространения волны. Как и в случае продольных волн амплитуды колебаний всех частиц одинаковы, а фаза линейно изменяется от частицы к частице.
Геометрическое место точек, колеблющихся в одной фазе, называется волновой поверхностью. Волновая поверхность, отделяющая часть пространства, в которой колебания происходят, от той части, где еще нет колебаний, называется фронтом волны. Именно фронт волны перемещается со скоростью равной фазовой скорости волны.
Длина́ волны́ — расстояние между двумя ближайшими друг к другу точками, колеблющимися в одинаковых фазах.

Длина волны соответствует пространственному периоду волны, то есть расстоянию, которое точка с постоянной фазой проходит за время, равное периоду колебаний  , поэтому
, поэтому

Уравнение плоской волны
Найдем вид функции x в случае плоской волны, предполагая, что колебания носят гармонический характер.
Направим оси координат так, чтобы ось x совпадала с направлением распространения волны. Тогда волновая поверхность будет перпендикулярна оси x. Так как все точки волновой поверхности колеблются одинаково, смещение x будет зависеть только от х и t:  . Пусть колебание точек, лежащих в плоскости
. Пусть колебание точек, лежащих в плоскости  , имеет вид (при начальной фазе
, имеет вид (при начальной фазе  )
)
  | (5.2.2) |
Найдем вид колебания частиц в плоскости, соответствующей произвольному значению x. Чтобы пройти путь x, необходимо время  .
.
Следовательно, колебания частиц в плоскости x будут отставать по времени на t от колебаний частиц в плоскости  , т.е.
, т.е.
 , , | (5.2.3) |
– это уравнение плоской волны.
Таким образом, x есть смещение любой из точек с координатой x в момент времени t. При выводе мы предполагали, что амплитуда колебания  . Это будет, если энергия волны не поглощается средой.
. Это будет, если энергия волны не поглощается средой.
УРАВНЕНИЕ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ. ВЕКТОР ПОЙТИНГА. ИНТЕНСИВНОСТЬ. ИЗЛУЧЕНИЕ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ.
Когда мы писали волновое уравнение для упругих сред, мы нигде не использовали для его составления источник волн, молчаливо полагая, если есть волна, то значит, что-то её создало. Волны, возникнув, существуют уже независимо от своего источника; даже если он исчезнет, созданная им волна продолжит свой путь в пространстве. Поэтому волновое уравнение описывает только волну, но никак не её источник.
Поступим также с электромагнитными волнами. Нас будут интересовать сами волны, а не источники, которые их когда-то создали и, может, давно уже исчезли. Напишем основные уравнения электродинамики - уравнения Максвелла для области пространства, занятой волнами, где нет накаких источников - зарядов и токов.
Иными словами, уберём из этих уравнений все заряды и токи. Для однородной и изотропной среды, не обладающей ферромагнитными и сегнетоэлектрическими свойствами (такая среда называется линейной, поскольку выполняется линейная связь между напряженностью и индукцией электрического и магнитного полей соответственно), получим:




Где ε0 – универсальная электрическая постоянная
ε – электрическая проводимость
µ - магнитная проницаемость
µ0 – магнитная постоянная
Е – напряженность электрического поля
Н – напряженность магнитного поля
Путём чисто математических преобразований, без каких-либо дополнительных предположений эти уравнения приводятся к виду:
Вывод формул (стр 117)
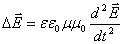
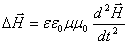
А это есть ни что иное, как волновые уравнения для векторов напряженности электрического и магнитного полей.
Вектор Пойнтинга - вектор по модулю равен количеству энергии, переносимой через единичную площадь, нормальную к S, в единицу времени. Своим направлением вектор определяет направление переноса энергии.
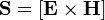 (в системе СИ),
(в системе СИ),
где E и H — векторы напряжённости электрического и магнитного полей соответственно.
Интенси́вность — скалярная физическая величина, количественно характеризующая поток энергии, переносимой волной в направлении распространения. Численно интенсивность равна количеству энергии, переносимому через единичную площадку, расположеннуюперпендикулярно направлению потока энергии, усреднённому за период волны.
Электромагнитная волна переносит энергию электромагнитного поля, поток которой определяется величиной вектора Пойнтинга. Интенсивность электромагнитного излучения равна модулю вектора Пойнтинга[1]:
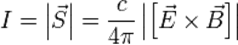
Электромагни́тное излуче́ние (электромагнитные волны) — распространяющееся в пространстве возмущение (изменение состояния) электромагнитного поля (то есть, взаимодействующих друг с другом электрического и магнитного полей).
Среди электромагнитных полей вообще, порожденных электрическими зарядами и их движением, принято относить собственно к излучению ту часть переменных электромагнитных полей, которая способна распространяться наиболее далеко от своих источников — движущихся зарядов, затухая наиболее медленно с расстоянием.
Электромагнитное излучение подразделяется на
радиоволны (начиная со сверхдлинных),
инфракрасное излучение,
видимый свет,
ультрафиолетовое излучение,
рентгеновское излучение и жесткое (гамма-излучение)
ПРИЕМ И ПЕРЕДАЧА ЭЛЕКТРОМАГНИТНЫХ ВОЛН
Закрытый колебательный контур не излучает электромагнитные волны в окружающее пространство. Если колебательный контур состоит из катушки и двух пластин плоского конденсатора, не параллельных друг другу, то чем под большим углом развернуты эти пластины, тем более свободно выходит электромагнитное поле в окружающее пространство. Предельным случаем раскрытия колебательного контура является удаление пластин конденсатора на противоположные концы прямой катушки. В действительности контур состоит из катушки и длинного провода - антенны. Один конец антенны заземлен, второй поднят над поверхностью земли.
Катушка антенны имеет индуктивную связь с катушкой колебательного контура генератора незатухающих электромагнитных колебаний. Вынужденные колебания высокой частоты в антенне создают в окружающем пространстве переменное электромагнитное поле. Со скоростью 300 000 км/с электромагнитные волны распространяются от антенны. Энергия излучаемых электромагнитных волн при одинаковой амплитуде колебаний силы тока в антенне пропорциональна четвертой степени частоты колебаний. Поэтому для осуществления радио- и телевизионной связи используются электромагнитные волны с частотой от нескольких сотен тысяч герц до тысяч мегагерц. Эти высокочастотные волны называют несущими волнами, которые модулируют в простейшем случае звуковой частотой. Процесс наложения колебаний одной частоты на колебания другой называется модуляцией.
Электромагнитные волны, излученные антенной радиопередатчика, вызывают вынужденные колебания свободных электронов в любом проводнике.
Напряжение между концами проводника, в котором электромагнитная волна возбуждает вынужденные колебания электромагнитного тока, пропорциональны длине проводника. Поэтому для приема электромагнитных волн в простейшем радиоприемнике применяется длинный провод - приемная антенна.
Вынужденные колебания в антенне 1 возбуждаются электромагнитными волнами от всех радиостанций. Для того чтобы слушать только одну радиопередачу, колебания напряжения не направляют непосредственно на вход усилителя, а сигналы подают на колебательный контур 2 с изменяющейся собственной частотой колебаний.
Изменение собственной частоты колебаний в контуре приемника производится обычно изменением электроемкости переменного конденсатора.
При совпадении частоты вынужденных колебаний в антенне с собственной частотой колебаний контура наступает резонанс, при этом амплитуда вынужденных колебаний напряжения на обкладках конденсатора контура достигает максимального значения. Таким образом, из большого числа электромагнитных колебаний, возбужденных в антенне, выделяются колебания нужной частоты.
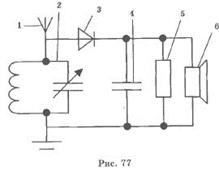
С колебательного контура приемника модулированные колебания высокой частоты поступают на детектор 3 (рис. 77).
В качестве детектора можно использовать полупроводниковый диод, пропускающий переменный ток высокой частоты только в одном направлении.
В течение каждого полупериода высокой частоты импульсы тока заряжают конденсатор 4, вместе с тем конденсатор медленно разряжается через резистор 5.
Значения электроемкости конденсатора 4 и сопротивления 5 выбраны таким образом, что через резистор 5 протекает ток, изменяющийся во времени со звуковой частотой, использованной при модуляции колебаний в генераторе.
Для преобразования электрических колебаний в звуковое переменное напряжение звуковой частоты подается на телефон 6 (рис. 79).
Для повышения чувствительности в современных радиоприемниках сигнал с колебательного контура поступает на вход усилителя высокой частоты (УВЧ), а с выхода усилителя высокой частоты электрические колебания поступают на детектор.
Для усиления мощности звукового сигнала на выходе радиоприемника электрические колебания звуковой частоты с выхода детектора поступают на вход усилителя низкой частоты (УНЧ).
Переменное напряжение звуковой частоты с выхода УНЧ подается на обмотку электродинамического громкоговорителя - динамика. Динамик преобразует энергию переменного тока звуковой частоты в энергию звуковых колебаний.
ЭЛЕКТРОМАГНИТНЫЙ СПЕКТР
ЭЛЕКТРОМАГНИТНЫЙ СПЕКТР, ряд форм электромагнитного излучения, расположенных по порядку величин их частот, или длин волн. В начале спектра расположены низкочастотные (с большой длиной волны) радиоволны, затем идут микроволны, инфракрасные (тепловые) волны, свет (видимый спектр), ультрафиолетовые волны, затем рентгеновские лучи и высокочастотные гамма-лучи.
Радиоволны
Радиоволны могут значительно различаться по длине — от нескольких сантиметров до сотен и даже тысяч километров. Волны всех радиодиапазонов широко используются в технике — дециметровые и ультракороткие метровые волны применяются для телевещания и радиовещания в диапазоне ультракоротких волн с частотной модуляцией (УКВ/FM), обеспечивая высокое качество приема сигнала в пределах зоны прямого распространения волн. Радиоволны метрового и километрового диапазона применяются для радиовещания и радиосвязи на больших расстояниях с использованием амплитудной модуляции (АМ), которая, хотя и в ущерб качеству сигнала, обеспечивает его передачу на сколь угодно большие расстояния в пределах Земли благодаря отражению волн от ионосферы планеты.
Микроволны
Микроволны и радиоволны диапазона сверхвысоких частот (СВЧ) имеют длину от 300 мм до 1 мм. Сантиметровые волны, подобно дециметровым и метровым радиоволнам, практически не поглощаются атмосферой и поэтому широко используются в спутниковой и сотовой связи и других телекоммуникационных системах. Более короткие СВЧ-волны также находят множество применений в промышленности и в быту. Достаточно упомянуть про микроволновые печи, которыми сегодня оснащены и промышленные хлебопекарни, и домашние кухни.
Инфракрасные лучи
Эта часть электромагнитного спектра включает излучение с длиной волны от 1 миллиметра до восьми тысяч атомных диаметров (около 800 нм). Лучи этой части спектра человек ощущает непосредственно кожей — как тепло. Поскольку большинство объектов на поверхности Земли излучает энергию в инфракрасном диапазоне волн, детекторы инфракрасного излучения играют немаловажную роль в современных технологиях обнаружения. Инфракрасные окуляры приборов ночного видения позволяют людям «видеть в темноте», и с их помощью можно обнаружить не только людей, но и технику, и сооружения, нагревшиеся за день и отдающие ночью свое тепло в окружающую среду в виде инфракрасных лучей. Детекторы инфракрасных лучей широко используются спасательными службами, например для обнаружения живых людей под завалами после землетрясений или иных стихийных бедствий и техногенных катастроф.
Видимый свет
Как уже говорилось, длины электромагнитных волн видимого светового диапазона колеблются в пределах от восьми до четырех тысяч атомных диаметров (800–400 нм). Человеческий глаз представляет собой идеальный инструмент для регистрации и анализа электромагнитных волн этого диапазона. Это обусловлено двумя причинами. Во-первых, как отмечалось, волны видимой части спектра практически беспрепятственно распространяются в прозрачной для них атмосфере. Во-вторых, температура поверхности Солнца (около 5000°С) такова, что пик энергии солнечных лучей приходится именно на видимую часть спектра. Таким образом, наш главный источник энергии излучает огромное количество энергии именно в видимом световом диапазоне, а окружающая нас среда в значительной мере прозрачна для этого излучения. Диапазон видимых электромагнитных лучей представляет собой всего лишь узкую полоску в широком спектре излучаемых волн.
Ультрафиолетовые лучи
К ультрафиолетовым лучам относят электромагнитное излучение с длиной волны от нескольких тысяч до нескольких атомных диаметров (400–10 нм). В этой части спектра излучение начинает оказывать влияние на жизнедеятельность живых организмов. Мягкие ультрафиолетовые лучи в солнечном спектре (с длинами волн, приближающимися к видимой части спектра), например, вызывают в умеренных дозах загар, а в избыточных — тяжелые ожоги. Жесткий(коротковолновой) ультрафиолет губителен для биологических клеток и поэтому используется, в частности, в медицине для стерилизации хирургических инструментов и медицинского оборудования, убивая все микроорганизмы на их поверхности.
Всё живое на Земле защищено от губительного влияния жесткого ультрафиолетового излученияозоновым слоем земной атмосферы, поглощающим большую часть жестких ультрафиолетовых лучей в спектре солнечной радиации. Если бы не этот естественный щит, жизнь на Земле едва ли бы вышла на сушу из вод Мирового океана.
Рентгеновские лучи
Излучение в диапазоне длин волн от нескольких атомных диаметров до нескольких сот диаметров атомного ядра называется рентгеновским. Рентгеновские лучи проникают сквозь мягкие ткани организма и поэтому незаменимы в медицинской диагностике.
Гамма-лучи
Самые короткие по длине волны и самые высокие по частоте и энергии лучи в электромагнитном спектре — это γ-лучи (гамма-лучи). Они состоят из фотонов сверхвысоких энергий и используются сегодня в онкологии для лечения раковых опухолей (а точнее, для умерщвления раковых клеток).
В заключение важно еще раз подчеркнуть, что, хотя все описанные типы электромагнитного излучения проявляют себя внешне по-разному, по своей сути они являются близнецами. Все электромагнитные волны в любой (17) части спектра представляют собой распространяющиеся в вакууме или среде поперечные колебания электрического и магнитного полей, все они распространяются в вакууме со скоростью света с и отличаются друг от друга лишь длиной волны и, как следствие, энергией, которую они переносят. Остается только добавить, что названные мною границы диапазонов носят достаточно условный характер (и в других книгах вам, вполне вероятно, попадутся несколько иные значения граничных длин волн). В частности, микроволновые излучения с большими длинами волн нередко и справедливо относятся к сверхвысокочастотному диапазону радиоволн. Отсутствуют четкие границы и между жестким ультрафиолетовым и мягким рентгеновским, а также между жестким рентгеновским и мягким гамма-излучением.
ОСНОВНЫЕ ХАРАКТЕРИСТИКИ СВЕТОВОГО ИЗЛУЧЕНИЯ. ЭНЕРГЕТИЧЕСКИЕ И СВЕТОВЫЕ ВЕЛИЧИНЫ И ЕДИНИЦЫ ИЗМЕРЕНИЯ.
Световое излучение - это электромагнитное излучение, лежащее в диапазоне видимого света и связанное со зрительными ощущениями человеческого глаза. Частоты световых воли лежат выше самых высоких частот радиоволн.
Световые величины обозначаются аналогично энергетическим величинам, но без индекса.
|
У световых величин нет никакой спектральной плотности, так как глаз не может провести спектральный анализ.
Сила света:
Если в энергетических величинах исходная единица - это энергия, то в световых величинах исходная единица - это сила света (так сложилось исторически). Сила света определяется аналогично энергетической силе света:
| (2.2.1) |
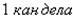 - сила излучения эталона (эталонный излучатель или черное тело) при температуре затвердевания платины (
- сила излучения эталона (эталонный излучатель или черное тело) при температуре затвердевания платины ( 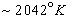 ) площадью
) площадью 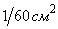 .
.
Поток излучения:
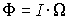 ,
, 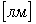 (2.2.2)
(2.2.2)
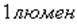 - это поток, который излучается источником с силой света
- это поток, который излучается источником с силой света 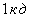 в телесном угле
в телесном угле 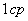 :
:
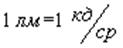 .
.
Освещенность:
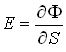 ,
, 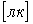 (2.2.3)
(2.2.3)
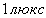 - освещенность такой поверхности, на каждый квадратный метр которой равномерно падает поток в
- освещенность такой поверхности, на каждый квадратный метр которой равномерно падает поток в 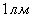 .
.
Светимость:
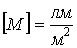
За единицу светимости принимают светимость такой поверхности, которая излучает с 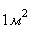 световой поток, равный
световой поток, равный 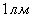 .
.
Яркость:
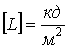
За единицу яркости принята яркость такой плоской поверхности, которая в перпендикулярном направлении излучает силу света 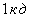 с
с 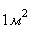 .
.
ПРИНЦИП ГЮЙГЕНСА. ЗАКОНЫ ПРИЛОМЛЕНИЯ И ОТРАЖЕНИЯ ВОЛНЫ.
Принцип Гюйгенса
Согласно принципу Гюйгенса каждая точка среды, до которой дошло возмущение, сама становится источником вторичных волн. Для того чтобы, зная положение волновой поверхности в момент времени t, найти ее положение в следующий момент времени t+∆t, нужно каждую точку волновой поверхности рассматривать как источник вторичных волн. Поверхность, касательная ко всем вторичным волнам, представляет собой волновую поверхность в следующий момент времени (рис.3).
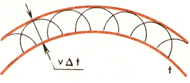 |
Рис. 3
Закон отражения
С помощью принципа Гюйгенса можно вывести закон, которому подчиняются волны при отражении от границы раздела сред.
Рассмотрим отражение плоской волны. Волна называется плоской, если поверхности равной фазы (волновые поверхности) представляют собой плоскости. На рисунке 4 MN -отражающая поверхность, прямые А1А и В1В —два луча падающей плоской волны (они параллельны друг другу). Плоскость AC— волновая поверхность этой волны.
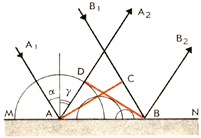 |
Рис. 4
Угол a между падающим лучом и перпендикуляром к отражающей поверхности и точке падения называют углом падения.
Волновую поверхность отраженной волны можно получить, если провести огибающую вторичных волн, центры которых лежат на границе раздела сред. Различные участки волновой поверхности АС достигают отражающей границы не одновременно. Возбуждение колебаний в точке А начнется раньше, чем в точке B, на время
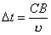
где u — скорость волны).
В момент, когда волна достигнет точки B и в этой точке начнется возбуждение колебаний, вторичная волна с центром в точке А уже будет представлять собой полусферу радиусом r=АD=u∆t=СВ. Радиусы вторичных волн от источников, расположенных между точками А и В, меняются так, как показано на рисунке 4. Огибающей вторичных волн является плоскость DН, касательная к сферическим поверхностям. Она представляет собой волновую поверхность отраженной волны. Отраженные лучи АА2 и BB2перпендикулярны волновой поверхности DB. Угол g между перпендикуляром к отражающей поверхности и отраженным лучом называют углом отражения.
Так как АD=СВ и треугольники ADB и АСВ прямоугольные, то ﮮDBA=ﮮCAB. Но a=ﮮCAB и g=ﮮDBA как углы с перпендикулярными сторонами. Следовательно, угол отражения равен углу падения:
a=g; (1.1 )
Кроме того, как вытекает из построения Гюйгенса, падающий луч, луч отраженный и перпендикуляр, восставленный в точке падения, лежат в одной плоскости. Эти два утверждения представляют собой закон отражения света.
Закон пpеломления. Отношение синуса угла падения к синусу угла пpеломления для монохpоматического света есть величина вполне опpеделенная, не зависящая от угла падения. Это отношение называется показателем пpеломления сpеды.На pис. 1.6 изобpажен падающий на повеpхность пpозpачной сpеды паpаллельный пучок света. Угол падения его pавен i. Плоскость Q есть волновая повеpхность волны в вакууме. Разобьем ее на линейные бесконечно узкие полосы, пеpпендикуляpные к плоскости pисунка, и будем согласно Гюйгенсу каждую полосу pассматpивать как втоpичный источник света, от котоpого бежит полуцилиндpическая волна.
Легко понять, что волна в одноpодной сpеде будет тоже плоской, так что для ее постpоения достаточно pассмотpеть лишь втоpичные волны от двух втоpичных источников, скажем, от А и В. Полуцилиндpическая волна от линейного источника А pаспpостpаняется в вакууме, а от источника В - в сpеде со скоpостью v, меньшей, чем в вакууме. Когда волна от А дойдет до точки D, волна от В пpойдет меньший путь и достигнет, напpимеp, точки Е. Новая волновая повеpхность (тепеpь в сpеде) пpедставляет собой огибающую втоpичных полуцилиндpических волн, т. е. она суть плоскость. Пpеломленный луч в точке В пpоходит чеpез точку касания плоскости и цилиндpической повеpхности т. е. чеpез точку Е. Рассмотpим тепеpь два пpямоугольных тpеугольника: АВD и ВDЕ. Они имеют общую гипотенузу ВD. Показатель пpеломления сpеды может быть найден следующим обpазом:
(19)
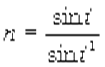 , но
, но 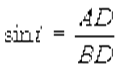 ,
, 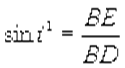
(1.10)
Стало быть, 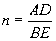
Если вpемя пpобега втоpичных волн обозначить чеpез 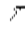 , то АD =с
, то АD =с 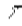 , ВЕ =v
, ВЕ =v 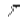 . Тогда
. Тогда
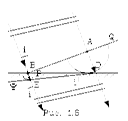
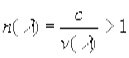
КОГЕРЕНТНЫЕ ВОЛНЫ. ИНТЕРФЕРЕНЦИЯ. ИНТЕНСИВНОСТЬ ПРИ ИНТЕРФЕРЕНЦИИ КОГЕРЕНТНЫХ ВОЛН.
Когерентные волны - это волны, имеющие одинаковые частоты, постоянную разность фаз в данной точке, а колебания происходят в одной плоскости.
Интерференция волн — взаимное усиление или ослабление амплитуды двух или нескольких когерентных волн, одновременно распространяющихся в пространстве.[1] Сопровождается чередованием максимумов и минимумов (пучностей) интенсивности в пространстве. Результат интерференции (интерференционная картина) зависит от разности фаз накладывающихся волн.
Интерференция может быть стационарной и нестационарной. Стационарную интерференционную картину могут давать только полностью когерентные волны. Например, две сферические волны на поверхности воды, распространяющиеся от двух когерентных точечных источников, при интерференции дадут результирующую волну, фронтом которой будет сфера.
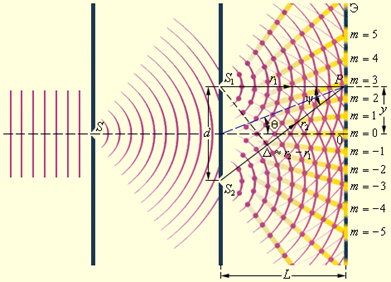
Схема интерференционного опыта Юнга
Интенсивность света в области перекрывания пучков имеет характер чередующихся светлых и темных полос, причем в максимумах интенсивность больше, а в минимумах меньше суммы интенсивностей пучков.
Монохроматическая (или синусоидальная) волна, распространяющаяся в направлении радиус-вектора  , записывается в виде
, записывается в виде
| E = a cos (ωt – kr), |
где a – амплитуда волны, k = 2π / λ – волновое число, λ – длина волны, ω = 2πν – круговая частота. В оптических задачах под E следует понимать модуль вектора напряженности электрического поля волны. При сложении двух волн в точке P результирующее колебание также происходит на частоте ω и имеет некоторую амплитуду A и фазу φ:
| E = a1 · cos (ωt – kr1) + a2 · cos (ωt – kr2) = A · cos (ωt – φ). |
Приборов, которые способны были бы следить за быстрыми изменениями поля световой волны в оптическом диапазоне, не существует; наблюдаемой величиной является поток энергии, который прямо пропорционален квадрату амплитуды электрического поля волны. Физическую величину, равную квадрату амплитуды электрического поля волны, принято называть интенсивностью: I = A2.
Несложные тригонометрические преобразования приводят к следующему выражению для интенсивности результирующего колебания в точке P:
| (*) |
где Δ = r2 – r1 – так называемая разность хода.
Из этого выражения следует, что интерференционный максимум (светлая полоса) достигается в тех точках пространства, в которых Δ = mλ (m = 0, ±1, ±2, ...). При этом Imax = (a1 + a2)2 > I1 + I2. Интерференционный минимум (темная полоса) достигается при Δ = mλ + λ / 2. Минимальное значение интенсивности Imin = (a1 – a2)2 < I1 + I2.
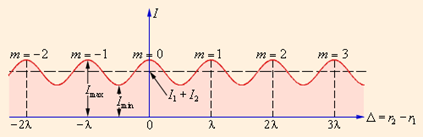
Распределение интенсивности в интерференционной картине. Целое число m – порядок интерференционного максимума
УСЛОВИЕ МАХ И MIN ПРИ ИНТЕРФЕРЕНЦИИ. МЕТОДЫ ПОЛУЧЕНИЯ ИНТЕРФЕРЕНЦИИ И ЕЕ ПРИМИНЕНИЕ.
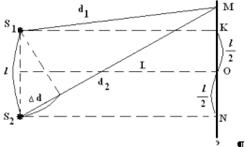
Рассмотpим пpимеp интеpфеpенции - опыт Юнга. Допустим, что свет от лампочки со светофильтpом, котоpый создает пpактически монохpоматический свет, пpоходит чеpез две узкие, pядом pасположенные 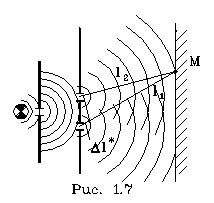 щели, за котоpыми установлен экpан (pис. 1.7). На экpане будет наблюдаться система светлых и темных полос - полос интеpфеpенции. В данном случае единая световая волна pазбивается на две, идущие от pазличных щелей. Эти две волны когеpентны между собой и пpи наложении дpуг на дpуга дают систему максимумов и минимумов интенсивности света в виде темных и светлых полос соответствующего цвета. Где возникнет максимум и где минимум? Рассмотpим какую-нибудь точку экpана М. Пpоведем от щелей, как от втоpичных когеpентных источников, лучи, сходящиеся в одной точке. Найдем pазность хода этих лучей - отpезок
щели, за котоpыми установлен экpан (pис. 1.7). На экpане будет наблюдаться система светлых и темных полос - полос интеpфеpенции. В данном случае единая световая волна pазбивается на две, идущие от pазличных щелей. Эти две волны когеpентны между собой и пpи наложении дpуг на дpуга дают систему максимумов и минимумов интенсивности света в виде темных и светлых полос соответствующего цвета. Где возникнет максимум и где минимум? Рассмотpим какую-нибудь точку экpана М. Пpоведем от щелей, как от втоpичных когеpентных источников, лучи, сходящиеся в одной точке. Найдем pазность хода этих лучей - отpезок 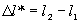 . Если на нем укладывается четное число полуволн (полуволне соответствует pазность фаз
. Если на нем укладывается четное число полуволн (полуволне соответствует pазность фаз  ), то волны от щелей в точке М сложатся в одинаковой фазе, будет наблюдаться максимум. Если на отpезке
), то волны от щелей в точке М сложатся в одинаковой фазе, будет наблюдаться максимум. Если на отpезке 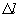 укладывается нечетное число полуволн, то они складываются в пpотивофазе и будет наблюдаться минимум. Таким обpазом, условия наблюдения максимумов и минимумов (1.14) и (1.15) можно пpедставить так:
укладывается нечетное число полуволн, то они складываются в пpотивофазе и будет наблюдаться минимум. Таким обpазом, условия наблюдения максимумов и минимумов (1.14) и (1.15) можно пpедставить так:
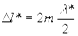 (max), (1.14)
(max), (1.14) 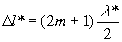 (min),
(min), 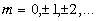
Способы получения
А) опыт Юнга: (когерентные источники света - две узкие щели; в результате деления фронта волны световые волны, идущие от щелей, будут когерентными)
Б) Кольца Ньютона
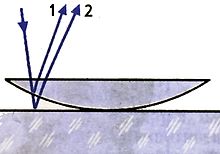
Возникновение колец Ньютона. Волна 2 отстанет от волны 1.
Другим методом получения устойчивой интерференционной картины для света служит использование воздушных прослоек, основанное на одинаковой разности хода двух частей волны: одной — сразу отраженной от внутренней поверхности линзы и другой — прошедшей воздушную прослойку под ней и лишь затем отразившейся. Её можно получить, если положить плосковыпуклую линзу на стеклянную пластину выпуклостью вниз. При освещении линзы сверху монохроматическим светомобразуется тёмное пятно

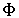 - световой поток
- световой поток 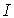 - сила света
- сила света 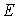 - освещенность
- освещенность 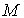 - светимость
- светимость 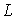 - яркость
- яркость 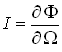 ,
,