Определение степени черноты твердого тела

цель работы

Усвоение и закрепление теоретического материала по разделу основы теории теплообмена "Лучистый теплообмен", а также овладение методом экспериментального определение коэффициента излучения и степени черноты твердого тела.

ЗАДАНИЕ

1. Экспериментальным путем определить коэффициент излучения и степень черноты твердого тела.

2. Найти погрешность полученного значения степени черноты по отношению к справочному значению (в процентах).

3. Сделать вывод по работе.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Все тела непрерывно излучают и поглощают тепловую энергию. Носителем лучистой тепловой энергии является электромагнитные колебания с длиной волны от 0.8 до 800 мкм. Процесс лучистого теплообмена происходит между телами, имеющими разное значение температур и разделенных газообразной средой.

Лучистый тепловой поток от тела, попав на другое тело, частично поглощается, частично отражается, а частично проходит через тело. Часть лучистой энергии, которая поглощается телом, снова превращается в тепловую энергию. Та часть энергии, которая отражается, попадает на другие (окружающие) тела и ими поглощается. То же самое происходит и с той частью энергии, которая проходит сквозь тело. Таким образом, после ряда поглощений излучаемая телом энергия полностью распределяется между окружающими телами. Следовательно, каждое тело не только непрерывно излучает, но и непрерывно поглощает лучистую энергию.

Для определения лучистого потока излучаемого телом, (Вт) используется формула

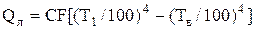, (1)

где С - коэффициент излучения серого тела, Вт/(м²×К⁴),

С = С_о×;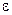

Со - коэффициент излучения абсолютно черного тела, Вт/(м²×К⁴),

С_о = 5.67;

e - степень черноты испытуемого тела;

F - площадь поверхности испытуемой трубки, м²;

Т₁- абсолютная температура поверхности испытуемой трубки, К;

Т_в- абсолютная температура воздуха в помещении, К.

Из формулы (1) определяется величина коэффициента излучения испытуемого тела, Вт/(м²×К⁴),

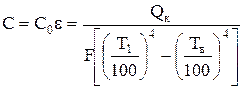. (2)

При рассмотрении лучистого теплообмена часть величин, входящих в расчетные формулы, определяется опытным путем; например степень черноты тела. Для определения опытным путем численной величины степени черноты тела, можно воспользоваться экспериментальной установкой.

ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА

Экспериментальная установка (рисунок) состоит из испытуемого 1 и эталонного 2 тел, выполненных в виде трубок длиною l, установленных вертикально. Наружные диаметры трубок одинаковы: d = 0.025 м.

Таким образом, испытуемое (серое) и эталонное (черное) тела имеют одинаковую величину поверхностей теплообмена F. Эталонная трубка покрыта :черным лаком с известной степенью черноты (e_эт = 0.97). Внутри трубок смонтированы электрические нагреватели 3, обеспечивающие равномерное выделение тепла по длине труб. Нагреватели питаются от сети переменного тока, их мощности регулируются лабораторными автотрансформаторами 4 и измеряются ваттметрами 5. Тепловой поток, создаваемый электронагревателем и проходящий через стенку трубы в окружающий воздух, определяется по мощности электронагревателя. Предотвращение утечек тепла в окружающий воздух торцы трубок достигается установкой теплоизоляционных заглушек.

Температура на поверхности трубок измеряется с помощью хромель-копелевых термопар 6 и микропроцессорного измерителя температур 7.

Температура воздуха в лаборатории определяется термометром, установленным вдали от установки. Предполагается, что температура тел в помещении (кроме тел 1 и 2) равна температуре воздуха в нем.

Тепловой поток с поверхности трубки к воздуху, определяемый в опыте, представляет собой сумму конвективного и лучистого тепловых потоков (Вт)

Q = Q_к + Q_л , (3)

тогда

Q_л = Q - Q_к . (4)

Значение Q_к можно рассчитать по формулам конвективного теплообмена, но удобнее эту величину исключить из рассмотрения за счет использования эталонного тела с известной степенью черноты. Для данной экспериментальной установки 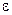_эт =0,97.

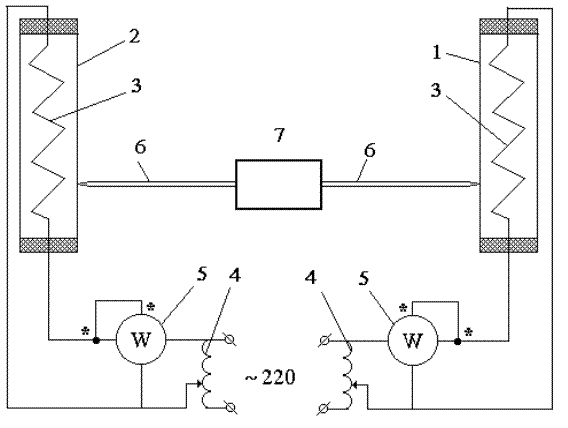
Рисунок. Схема экспериментальной установки

Излучение эталонного тела будет определяться по формуле

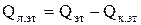. (5)

Если форма, размер и температуры испытуемого и эталонного тел одинаковы, конвективные составляющие можно приравнять, т.е.

_,

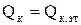тогда

Q_л = Q – 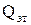+ 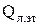_. = (Q – 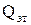) + 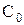eF[( 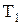/100)⁴ – (T_в /100)⁴] . (6)

Подставив (6) в (2), получим расчетную формулу

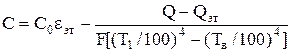. (7)

ПРОВЕДЕНИЕ ОПЫТА

1. Включить установку поворотом ручки на щите в положение "I".

2. Поворотом ручек автотрансформаторов установить одинаковые для обеих трубок мощности нагревателей (по указанию преподавателя).

3. Дождаться стабилизации температур для испытуемой и эталонной трубок.

4. Регулируя напряжение на нагревателе эталонного цилиндра и наблюдая за изменением его температуры, добиться равенства температур обеих трубок в стационарном тепловом режиме.

5. При наступлении стационарного теплового режима показания приборов записать в таблицу.

Т а б л и ц а

Номера опытов	Испытуемое тело W, Вт	Эталонное тело Wэт, Вт	t1, °C	tв,°С

6. Поворотом ручки на щите в положение "0" выключить установку.

ОБРАБОТКА ОПЫТНЫХ ДАННЫХ

1. Определить тепловые потоки с поверхности испытуемой и эталонной трубок, которые принять равными мощностям электронагревателей внутри трубок (Вт) Q = W, Q_эт = W_эт.

2. Определить площадь поверхности трубки (м²), где F = pdl, d = 0.025м, l = 0.42 м.

3. Определить коэффициент излучения С испытуемого тела по формуле (7).

4. Вычислить степень черноты испытуемого тела при температуре поверхности t₁, °C

e = C / C₀

5. Из справочных таблиц (см. приложение) находится значение степени черноты испытуемого материала e_таб.

6. Определить погрешность найденной в эксперименте степени черноты материала по отношению к справочному значению e_таб по формуле

.

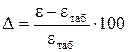7. Сделать вывод по работе.

ВОПРОСЫ ДЛЯ САМОСТОЯТЕЛЬНОЙ ПОДГОТОВКИ

1. Установившийся и неустановившийся тепловой режим.

2. Физическая сущность лучистого теплообмена.

3. Понятия: абсолютно черное, белое, и прозрачное тела, серое тело.

4. Основные законы излучения и поглощения лучистой энергии различными телами.

5. Коэффициент излучения абсолютно черного и серого тел.

6. Степень черноты тела.

7. Лучистый теплообмен между твердыми телами.

8. Приведенная степень черноты системы.

9. Сущность способа определения коэффициента излучения тепла методом сравнения с эталонным телом. БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Баскаков А.П. и др. Теплотехника.- М. Энергиздат, 1982.

2. Исаченко В.П., Осипова В.А., Сукомел А.С. Теплопередача.- М.: Энергия,1981.

3. Михеев М.А., Михеева И.М. Основы теплопередачи.- М.: Энергия, 1977.

4. Нащокин В.В. Техническая термодинамика и теплопередача.- М.: Высшая школа, 1980.

Приложение

Степень черноты нормального излучения для различных материалов

Наименование материала	t, °С	e
Алюминий полированный	225-572	0.039-0.057
Алюминий шероховатый		0.055
Алюминий, окисленный при 600 °С	200-600	0.11-0.19
Железо полированное	425-1020	0.144-0.377
Железо, свежеобработанное наждаком		0.242
Железо окисленное		0.736
Железо окисленное гладкое	125-525	0.78-0.82
Железо литое необработанное	925-1115	0.87-0.95
Стальное литье полированное	770-1040	0.52-0.56
Сталь листовая шлифованная	940-1100	0.55-0.61
Сталь, окисленная при 600 °С	200-600	0.80
Сталь листовая с плотным блестящим слоем окиси		0.82
Латунная пластина, прокатанная с естественной поверхностью		0.06
Латунная пластина, прокатанная, обработанная грубым наждаком		0.20
Латунная пластина тусклая	50-350	0.22
Латунь, окисленная при 600 °С	200-600	0.61-0.59
Медь, тщательно полированная, электролитная	80-115	0.018-0.023
Медь торговая, шабреная до блеска, но не зеркальная		0.072
Медь, окисленная при 600 °С	200-600	0.57-0.87
Лак белый эмалевый, на железной шероховатой пластине		0.906
Лак черный блестящий, распыленный на железной пластине		0.875
Лак черный матовый	40-95	0.96-0.98
Лак белый
Шеллак черный блестящий, на луженом железе	40-95	0.80-0.95
Шеллак черно-матовый		0.821
Масляные краски различных цветов	75-145	0.91
Штукатурка шероховатая, известковая	10-88	0.92-0.96 0.91

РАБОТА № 9

ИССЛЕДОВАНИЕ ТЕПЛООТДАЧИ ЦИЛИНДРА

В СВОБОДНОМ ПОТОКЕ ВОЗДУХА

цель работы

Усвоение и закрепление теоретического материала по разделу теплопередачи "Конвективный теплообмен", овладение методом экспериментального определения коэффициента теплоотдачи при свободном движении (конвекции) жидкости.

ЗАДАНИЕ

1. Экспериментальным путем определить коэффициент теплоотдачи от поверхности горизонтального цилиндра к воздуху в условиях его свободного движения при различных температурных напорах между поверхностью цилиндра и воздухом.

2. Построить графическую зависимость коэффициента теплоотдачи от температурного напора.

3. Для условий одного-двух опытов вычислить значение коэффициента теплоотдачи, используя расчетное критериальное значение.

4. Вычислить погрешность найденного в опыте значения коэффициента теплоотдачи по отношению к расчетному.

5. Сделать вывод по работе.

ВОПРОСЫ ДЛЯ САМОСТОЯТЕЛЬНОЙ ПОДГОТОВКИ

1. Установившийся и неустановившийся тепловые режимы.

2. Физическая сущность процесса конвективной передачи.

3. Уравнение Ньютона-Рихмана. Коэффициент теплоотдачи; факторы, влияющие на величину коэффициента теплоотдачи.

4. Свободное и вынужденное движение жидкости.

5. Сущность теории подобия, критерия теплового подобия, их физический смысл.

6. Понятия: определяющая температура, определяющий размер.

7. Критериальные уравнения в неявном виде для различных случаев конвективной передачи, их анализ.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Конвективная теплоотдача – это теплообмен между поверхностью твердого тела и окружающей это тело жидкостью. Тепло в данном случае распространяется одновременно теплопроводностью и конвекцией жидкости. Тепловой поток при конвективной теплоотдаче (Вт) подсчитывается по формуле Ньютона-Рихмана

Q = aFDt

где F - поверхность твердого тела участвующая в теплообмене, м²;

t = (t_с - t_o) -температурный напор между поверхностью твердого тела и окружающей тело жидкостью, °С;

a - коэффициент теплоотдачи, Вт/(м²×°С).

При практических расчетах вся сложность их проведения сводится к определению численной величины коэффициента теплоотдачи a, поскольку эта величина зависит от большого числа факторов, определяющих процесс теплоотдачи. В общем случае коэффициент теплоотдачи является функцией физических параметров жидкости, характера течения и режима движения жидкости, формы, размеров, расположения тела и др.

При изучении различных физических явлений применяют два метода исследования, которые позволяют получить количественные закономерности для исследуемых явлений. В первом методе используют экспериментальное изучение конкретных свойств, единичного явления, во втором исходят из теоретического исследования рассматриваемой проблемы. Однако оба метода имеют недостатки. Недостатком экспериментального метода исследования является невозможность распространения результатов, полученных в данном опыте, на другие явления, отличающиеся от изученного. Недостатком теоретического исследования является невозможность перейти от класса явлений, характеризуемых дифференциальными уравнениями и условиями однозначности, к единичному конкретному явлению. Поэтому каждый из методов в отдельности не может быть эффективно использован для решения практических задач.

Для нахождения численной величины коэффициента теплоотдачи используют уравнения теории подобия (критериальные уравнения). Теория теплового подобия это теоретическая база для постановки опытов и обработки экспериментальных данных.

Для теплообмена при свободном движении жидкости в неограниченном пространстве критериальное уравнение имеет вид

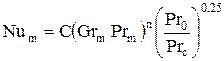(1)

Для газа уравнение (1) преобразуется к виду

Nu_m = C (Gr_mPr_m)ⁿ (2)

Численные значения критериев определяются по следующим формулам:

Nu_m = a l₀ / l_m– критерий Нуссельта;

Gr_m = b gl₀³Dt / n_m² – критерий Грасгофа;

Pr_m = g_m / a_m– критерий Прандтля.

В указанные критерии входят величины:

l₀ - определяющий размер, м (для горизонтальной трубки l₀ = d, для вертикальной l₀ = h );

l_m - коэффициент теплопроводности жидкости Вт/(м×°С );

n_m - коэффициент кинематической вязкости жидкости, м /с;

b = 1/(t_m+273) - коэффициент объемного расширения, 1/град;

Dt = t_c – t₀ - температурный напор между стенкой и жидкостью, °С.

В уравнениях (1) и (2) индекс "m" указывает на то, что за определяющую температуру (°С) принята среднеарифметическая температура

t_m = 0.5(t_c + t₀).

ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА

Экспериментальная установка (рисунок) состоит из трубки 1, внутри которой находится электронагреватель 2. Величина теплового потока, который отводится от наружной поверхности трубы, регулируется автотрансформатором 3 и определяется по показаниям вольтметра 4 и амперметра 5. Разность между температурами стенки трубы и окружающего воздуха измеряется с помощью дифференциальной термопары 6 и милливольтметра 7. По результатам измерений определяются конвективная составляющая теплового потока, и рассчитывается коэффициент теплоотдачи.

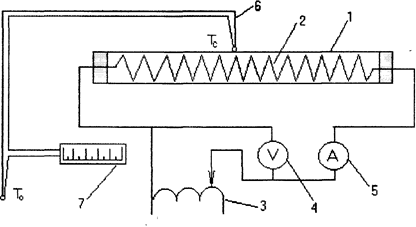
Рисунок. Схема экспериментальной установки

ПРОВЕДЕНИЕ ОПЫТА

1. Включить установку в сеть, повернув ручку на щите в положение "1".

2. Поворачивая ручку автотрансформатора, установить заданную преподавателем мощность нагревателя.

3. Наблюдая за показаниями вольтметра, дождаться установления стационарного теплового режима и записать показания приборов в таблицу наблюдений.

4. Опыты повторить при нескольких различных значениях мощности нагревателя.

Т а б л и ц а 1

№ опыта	U, B	I, А	DE, мВ	DT, К	Тс, K

ОБРАБОТКА ОПЫТНЫХ ДАННЫХ

1. Вычислить полный поток тепла, передаваемый путем конвекции и излучения, Вт

Q = UI

где U-напряжение, В I-сила тока, А

2. Вычислить лучистую составляющую теплового потока, Вт

,

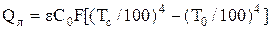где e = 0.5 - степень черноты поверхности испытуемой трубы;

С_о=5.67- коэффициент излучения абсолютно черного тела, Вт/(м²×К⁴);

F = pdl - площадь поверхности трубы, излучающей тепло в окружающий воздух, м², d = 0.013;

l = 0.780 - диаметр и длина трубы, м;

Т_о - температура окружающего воздуха. К;

Т_c - температура стенки трубы. К;

DT - температурный напор между поверхностью трубы и окружающим воздухом. К;

DЕ - термоЭДС дифференциальной хромель-капелевой термопары, мВ.

3. Вычислить конвективную составляющую теплового потока, Вт

Q_к = Q - Q_л

4. Вычислить экспериментальное значение коэффициента теплоотдачи, Вт / ( м²×К)

a_э = Q_к / (FDt)

5. Аналогичным образом производится обработка данных для второго и последующих опытов.

6. По данным опытов строится графическая зависимость

a_э = j(Dt)

7. По условиям одного из опытов вычислить коэффициент теплоотдачи на основании решения расчетного критериального уравнения (2).

Последовательность расчетов следующая.

Найти численное значение определяющей температуры, °С

t_m = 0,5(t_c + t₀)

По найденному значению t_m из таблицы 2 выбрать значение констант жидкости l_m, n_m, a_­m.

Вычислить значение критериев Грасгофа и Прандтля.

Определить режим движения жидкости при свободной конвекции по величине произведения(Gr_mPr_m) и по найденному его из таблицы 3 принять значения коэффициента С и показателя степени n.

Найдя численные значения Nu_m и учитывая, что критерий Нуссельта определяется по формуле

Nu_m = al₀ / l_m

Определить расчетное значение коэффициента теплоотдачи a, Вт/(м²×°С)

Т а б л и ц а 2

tm, °С	l ´102, Вт/(м×К)	а ´106, м2/с	n ´ 106, м2/с
	2.51	20.0	14.16
	2.59	21.4	15.06
	2.67	22.9	16.00
	2.76	24.3	16.90
	2.83	25.7	17.95
	2.90	27.2	18.97
	2.96	28.6	20.02
	3.05	30.2	21.09
	3.13	31.9	22.10
	3.21	33.6	23.13

Т а б л и ц а 3

(Grm Prm )	С	n
1´10-3 ¸5´102	1.18	0.125
5´102 ¸ 2´107	0.54	0.25
2´107 ¸ 1´1013	0.135	0.33

1. Определить погрешность найденного в эксперименте значения коэффициента теплоотдачи a_э по отношению к расчетному значению a по формуле, %

.

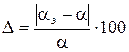2. Сделать вывод по работе.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Михеев М. А., Михеева И.М. Основы теплопередачи.- М.: Энергия,1977.

2. Баскаков А.П. и др. Теплотехника.- М.:Энергоиздат,1982.

3. Нащокин В. В. Техническая термодинамика и теплопередача.- М.:1980.

4. Исаченко В.П., Осипова В.А., Сукомел А.С. Теплопередача.- М.: Энергия,1981.

РАБОТА № 10

ИССЛЕДОВАНИЕ ТЕПЛООТДАЧИ ЦИЛИНДРА

ПРИ ВЫНУЖДЕННОМ ДВИЖЕНИИ ЖИДКОСТИ

ЦЕЛЬ РАБОТЫ

Усвоение теоретического материала по разделу теплопередачи "Конвективный теплообмен", а также овладение методом экспериментального определения коэффициента теплоотдачи при вынужденном движении жидкости.

ЗАДАНИЕ

1. Экспериментально определить коэффициент теплоотдачи от поверхности цилиндра к воздуху в условиях его вынужденного движения (поперечное омывание) при различных температурных напорах между поверхностью цилиндра и воздухом (три-четыре опыта).

2. Построить графическую зависимость коэффициента теплоотдачи от температурного напора.

3. Вычислить значения коэффициента теплоотдачи, используя критериальные уравнения.

4. Вычислить погрешность найденного в опыте значения коэффициента теплоотдачи по отношению к расчетному.

5. Сделать вывод по работе.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Конвективная теплоотдача – это теплообмен между поверхностью твердого тела и окружающей это тело жидкостью за счет одновременной теплопроводности и конвекции жидкости.

Тепловой поток при конвективной теплоотдаче Q, Вт, определяется по формуле Ньютона-Рихмана

Q = aFDt,

где a - коэффициент конвективной теплоотдачи, Вт/(м²×⁰С);

F – площадь поверхности твердого тела, участвующего в теплообмене, м²;

Dt = t_c – t_о – температурный напор между поверхностью твердого тела и окружающей тело жидкостью, ⁰С.

При проведении теплотехнических расчетов вся сложность процесса сводится к вычислению величины коэффициента теплоотдачи a, т.к. эта величина зависит от большого числа факторов, определяющих процесс теплоотдачи. Коэффициент теплоотдачи является функцией физических параметров жидкости, характера течения и режима движения жидкости, формы, размеров, расположения твердого тела и многих других факторов.

При изучении различных физических явлений одним из методов получения количественных закономерностей является эксперимент. Недостатком этого метода является невозможность распространения результатов, полученных в данном опыте, на другие явления, чем-то отличающиеся от изученного.

Недостаток теоретического исследования процесса заключается в невозможности перехода от класса явлений, характеризуемых дифференциальными уравнениями и условиями однозначности, к единичному конкретному явлению. Поэтому каждый из этих методов в отдельности не может быть эффективно использован для решения практических задач.

При решении задач конвективного теплообмена для нахождения численной величины коэффициента теплоотдачи используют уравнения теории теплового подобия (критериальные уравнения). Для теплообмена при вынужденном движении жидкости в случае поперечного обтекания одиночного цилиндра критериальные уравнения имеют вид:

При Rе = 1´10 ¸ 1´10⁵

Nu = 0.5Re^0.5Pr^0.38(Pr₀ / Pr_c)^0.25. (1)

При Re = 1´10³ ¸2´10⁵

Nu = 0.25Re^0.6Pr^0.38(Pr₀ / Pr_c)^0.25. (2)

Численные значения критериев подобия определяются следующим образцом:

Nu = al_o / l_m – критерий Нуссельта;

Re = wl_o / n_m – критерий Рейнольдса;

Рr = n_m / а_m – критерий Прандтля.

В указанные критерии входят величины:

l_o – определяющий размер, м (для горизонтальной трубки l_o = d_н, для вертикальной l_o = h);

l_m – коэффициент теплопроводности жидкости, Вт/(м²×⁰С);

w – линейная скорость движущейся жидкости, м/с;

n_m – коэффициент кинематической вязкости жидкости, м²/с;

а_m – коэффициент температуропроводности жидкости, м²/с.

ПРИМЕЧАНИЕ. Индекс "m" указывает на то, что за определяющую температуру t, ⁰С, принята среднеарифметическая температура t_m = 0.5(t_c + t₀).

Формулы (1) и (2) справедливы для любых жидкостей: для воздуха эти закономерности упрощаются и принимают соответственно вид:

Nu_m = 0.43Re_m^0.5 (3)

и

Nu_m = 0.216Re_m^0.6. (4)

ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА

Тепловой поток, источником которого является электронагреватель 1 (рисунок), отводится от наружной поверхности трубки 2 путем загруженной конвекции и излучения. Величина теплового потока регулируется автотрансформатором 3 и определяется по показаниям вольтметра 4 и амперметра 5. Скорость воздушного потока в коробке 6 регулируется путем изменения автотрансформатором 7 числа оборотов вентиляторов 8 и измеряется анемометром 9 после выравнивающей поток сетки 10. Разность между температурами стенки трубки и окружающего воздуха измеряется с помощью батареи дифференциальных термопар 11 и вольтметра 12. По результатам измерений при различных значениях мощности нагревается и скорости воздушного потока определяется конвективная составляющая теплового потока и рассчитывается коэффициент теплоотдачи.

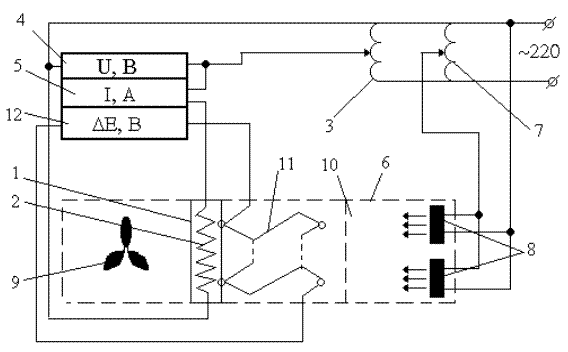
Рисунок. Схема экспериментальной установки

ПРОВЕДЕНИЕ ОПЫТА

1. Включит установку в сеть, повернуть ручку на щите в положение "1".

2. Поворачивая ручку автотрансформатора 3, установить заданную преподавателем мощность нагревателя.

3. Поворачивая ручку автотрансформатора 7, установить скорость движения воздуха в канале ~ 2 м/с.

4. Наблюдая за показаниями вольтметра 12, дождаться установления стационарного теплового режима и записать показания приборов в табл. 1.

5. Опыт повторить при других значениях мощности нагревателя и скорости.

Т а б л и ц а 1

Номер опыта	W, м/с	U, B	I, А	DE, мВ	Tс, К	DT, К	a, Вт/(м2×К)	Re	Nu

ОБРАБОТКА ОПЫТНЫХ ДАННЫХ

1. Вычислить полный тепловой поток Q, Вт,

Q = UI,

где U – напряжение, В;

I – сила тока, А.

2. Вычислить лучистую составляющую теплового потока Q_л, Вт,

Q_л = eC₀F[(T_c/100)⁴ – (T_o/100)⁴] ,

e = 0.5 – степень черноты трубы;

C₀ = 5.67 – коэффициент излучения абсолютного черного тела, Вт/(м²×К⁴);

F = pd_нl – площадь поверхности цилиндра, м²;

d_н = 0.013 м, l = 0.3 м – диаметр и длина цилиндра;

T₀ – температура окружающего воздуха, К;

T_c = T_o + DT – средняя температура стенки цилиндра, К;

DT = 1,48DЕ – средний температурный напор между поверхностью цилиндра и окружающим воздухом, К;

DE – темоЭДС батареи дифференциальных хромель-копелевых термопар, мВ.

3. Вычислить конвективную составляющую теплового потока Q_к, Вт,

Q_к = Q – Q_л.

4. Вычислить экспериментальное значение коэффициента теплоотдачи

a_э, Вт/(м²×К),

a_э = Q_к/(FDТ).

5. Аналогичным образом производится обработка данных для второго и последующих опытов.

6. По данным опытов строится графическая зависимость

a_э = j(DТ).

7. По условиям опытов вычислить коэффициент теплоотдачи на основании решения расчетного критериального уравнения (3) или (4).

Последовательность расчетов следующая.

Найти численное значение определяющей температуры, ⁰С

t_m = 0,5(t_с + t₀).

По найденному значению t_m из табл. 2 выбрать значение констант жидкости l_m, n_m.

Т а б л и ц а 2

t, 0С
l×102, Вт/(м×К)	2.51	2.59	2.67	2.76	2.83	2.90	2.96	3.05	3.13	3.21
n×106, м2/с	14.6	15.06	16.00	16.90	17.95	18.97	20.02	21.09	22.10	23.13

Вычислить значение критерия Рейнольдса и выбрать расчетное уравнение.

Вычислить критерий Нуссельта, и используя его значение, определить расчетный коэффициент теплоотдачи a_р, Вт/(м²×К)

a_р = Nu_m×l_m /d .

8. Определить погрешность (%) найденного в эксперименте значения коэффициента теплоотдачи a_э по отношению к расчетному значению a_р по формуле

D = (a_э - a_р­)100/a_р .

9. Сделать вывод по работе.

ВОПРОСЫ ДЛЯ САМОСТОЯТЕЛЬНОЙ ПОДГОТОВКИ

1. Неустановившийся и установившийся тепловые режимы.

2. Физическая сущность и механизм процессе конвективной теплоотдачи.

3. Уравнение Ньютона-Рихмана, его анализ. Коэффициент теплоотдачи: факторы, влияющие на величину коэффициента теплоотдачи.

4. Свободное и вынужденное движение жидкости.

5. Особенности процесса теплоотдачи при поперечном омывании одиночного цилиндра и пучка труб.

6. Сущность теории подобия, критерии теплового подобия, их физический смысл.

7. Понятие: определяющая температура, определяющий размер.

8. Критериальные уравнения в неявном виде для различных случаев конвективной теплоотдачи, их анализ.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Михеев М.А., Михеева И.М. Основы теплопередачи.- М.: Энергия, 1977.

2. Нащокин В.В. Техническая термодинамика и теплопередача.- М.: Высшая школа, 1980.

3. Баскаков А.П. и др. Теплотехника.- М.: Энергоиздат, 1982.

4. Исаченко В.П., Осипова В.А., Сукомел А.С. Теплопередача.- М.: Энергия, 1987.

Учебное издание

Лабораторный практикум

по курсам "Теплотехника", "Тепло- и хладотехника",

"Энерготехнология химических производств", "Термодинамика",

"Моделирование теплообменных процессов"

Для студентов специальностей

270100, 270300, 270400, 270500, 270900, 271100,

170600, 170500, 071900, 320700, 210200

Составители ХАРИН Владимир Михайлович,

шишацкий Юлиан Иванович,

семенихин Олег Александрович,

панфилов Юрий Владимирович,

ТОЛСТОВ Сергей Анатольевич

Редактор Н.А. Сотникова

Корректор Н.В. Бургонова

ЛР № 020449 от 31.10.97. Подп. в печать 2001.

Формат 60´84/16. Офсетная печать.

Бумага для множ. аппаратов. Усл. п. л. 4. Уч.- изд. л. 3.8.

Тираж 300 экз. Изд. № . Заказ .С –

Воронежская государственная технологическая академия

Участок оперативной полиграфии (ВГТА)

Адрес академии и участка оперативной полиграфии:

394017 Воронеж, пр. Революции, 19