Принципы решения прямых и обратных задач магниторазведки
Основные положения теории магниторазведки.
При магниторазведке рассчитываются аномалии полного вектора 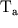 (4.1.1) или его составляющих
(4.1.1) или его составляющих 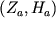 путем исключения из наблюденного поля нормального поля и вариаций. Поэтому в теории магниторазведки определяются эти параметры для объектов с разной интенсивностью и направлением намагничения (
путем исключения из наблюденного поля нормального поля и вариаций. Поэтому в теории магниторазведки определяются эти параметры для объектов с разной интенсивностью и направлением намагничения ( 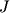 ). Для простоты решения можно считать
). Для простоты решения можно считать 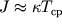 , где
, где  - магнитная восприимчивость объекта,
- магнитная восприимчивость объекта, 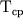 - средняя напряженность геомагнитного поля в месте его расположения, а остаточной намагниченностью
- средняя напряженность геомагнитного поля в месте его расположения, а остаточной намагниченностью 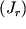 пренебречь.
пренебречь.
Основной закон магнетизма был сформулирован Кулоном, который предполагал, что существование магнетизма связано с наличием магнитных масс, положительных и отрицательных. Между двумя магнитными массами 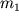 и
и 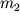 , помещенными в среду с магнитной проницаемостью
, помещенными в среду с магнитной проницаемостью 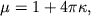 действует сила
действует сила 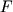 , которая определяется законом Кулона
, которая определяется законом Кулона 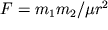 , где
, где  - расстояние между центрами магнитных масс.
- расстояние между центрами магнитных масс.
Последующим развитием физики было доказано, что магнитных масс, как самостоятельных субстанций, в природе не существует, а магнитные свойства тел являются следствием движения электрически заряженных частиц в атомах вещества. Одни вещества способны под действием магнитного поля упорядочивать движения зарядов и намагничиваться, другие нет. Хотя магнитных масс в природе нет, но в теории магнетизма законом Кулона формально продолжают пользоваться. При этом под магнитной массой одного знака понимается произведение интенсивности намагничения ( 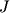 ) на площадь намагниченного тела (
) на площадь намагниченного тела ( 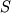 ), перпендикулярную этому вектору (
), перпендикулярную этому вектору ( 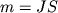 ).
).
Любое намагниченное тело можно представить сочетанием двух таких магнитных масс, находящихся на противоположных частях тела - полюсах. Северным (положительным) полюсом намагниченного тела (например, магнитной стрелки) считается тот, который поворачивается в сторону северного географического полюса, если дать возможность телу свободно вращаться вокруг вертикальной оси. Как отмечалось выше, при таком определении магнитный полюс Земли, находящийся в северном полушарии, обладает южным (отрицательным) магнетизмом, поскольку притягиваются магнитные массы противоположного знака, а массы одного и того же знака отталкиваются.
В теории магниторазведки, как и в любых других методах геофизики, решаются прямые и обратные задачи. Прямой задачей магниторазведки называется нахождение магнитных аномалий ( 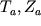 и др.) над объектами известной формы, глубины залегания и намагниченности. Обратной задачей магниторазведки является определение формы, глубины залегания, намагниченности по измеренному площадному распределению аномалий.
и др.) над объектами известной формы, глубины залегания и намагниченности. Обратной задачей магниторазведки является определение формы, глубины залегания, намагниченности по измеренному площадному распределению аномалий.
Поле магнитного диполя.
Для облегчения решения задач магниторазведки вводится понятие магнитного потенциала точечной магнитной массы
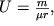 | (2.4) |
где  - расстояние от центра магнитной массы до точки наблюдения.
- расстояние от центра магнитной массы до точки наблюдения.
В теории магнетизма пользуются понятием магнитного диполя, т.е. двух равных, близко расположенных магнитных масс противоположного знака (рис. 2.3). Потенциал диполя 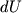 выражается формулой
выражается формулой
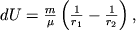 |
где 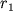 и
и 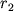 - расстояния от центра магнитных масс до точки наблюдения.
- расстояния от центра магнитных масс до точки наблюдения.
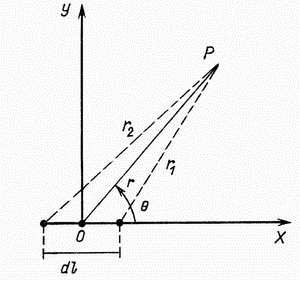 |
| Рис. 2.3. Магнитный диполь |
Выразив с помощью теоремы косинусов 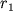 и
и 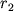 через
через  ,
, 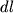 , и
, и 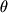 , можно записать
, можно записать
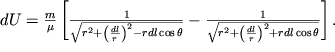 |
Разделив числитель и знаменатель на  и используя формулу бинома Ньютона, получим
и используя формулу бинома Ньютона, получим
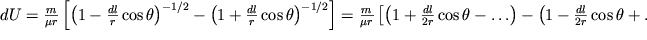 |
Поскольку 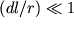 , то всеми степенями выражения
, то всеми степенями выражения 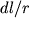 , большими единицы, можно пренебречь, и формула потенциала диполя упростится:
, большими единицы, можно пренебречь, и формула потенциала диполя упростится:
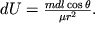 |
Или, заменив 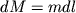 , получим окончательное выражение для потенциала диполя
, получим окончательное выражение для потенциала диполя
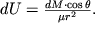 |
Из выражения для потенциала диполя нетрудно получить составляющие поля 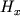 и
и 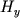 и полный (
и полный ( 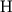 ) вектор напряженности. Заменив
) вектор напряженности. Заменив  можно записать:
можно записать:
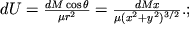 |
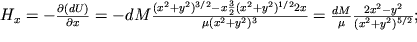 | (2.5) |
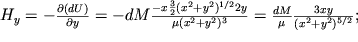 |
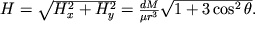 |
В частности, на протяжении оси диполя ( 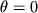 )
) 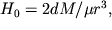 на перпендикуляре к оси диполя, в его центре
на перпендикуляре к оси диполя, в его центре 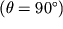
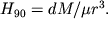
Реальные магнитные тела можно рассматривать как совокупность элементарных магнитных диполей.
Интенсивность намагничения элементарного объема ( 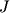 ), согласно определению, равна отношению магнитного момента (
), согласно определению, равна отношению магнитного момента ( 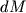 ) к его объему (
) к его объему ( 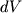 ). Поэтому выражение для потенциала магнитного диполя перепишется в следующем виде:
). Поэтому выражение для потенциала магнитного диполя перепишется в следующем виде: 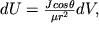 где вектор
где вектор 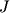 направлен вдоль оси диполя.
направлен вдоль оси диполя.
Mагнитный потенциал любого тела можно представить в виде интеграла по объему этого тела от потенциалов элементарных диполей, из которых состоит данное тело:
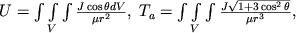 | (2.6) |
где интегрирование ведут по всему объему тела ( 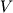 ).
).
Эти уравнения лежат в основе всей теории магниторазведки. Аналитические выражения при решении уравнений (2.6) получаются лишь для тел простой геометрической формы и однородной (постоянной) намагниченности. Для тел более сложной формы, да еще при разной намагниченности, возможны численные решения с помощью ЭВМ. Рассмотрим решение прямых и обратных задач для некоторых простейших тел: вертикального бесконечного столба (стержня), шара, пласта и горизонтального цилиндра бесконечного простирания для случая их вертикальной намагниченности. Допущение вертикальной намагниченности не только упрощает решение задач, но и является вполне обоснованным, поскольку намагниченность горных пород при широте, большей 40 - 45  , близка к вертикальной. Кроме того, при расчетах можно считать, что
, близка к вертикальной. Кроме того, при расчетах можно считать, что 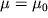 , где
, где 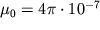 - магнитная проницаемость воздуха.
- магнитная проницаемость воздуха.
