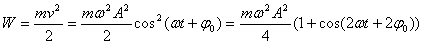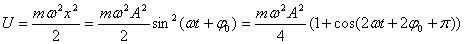Энергия гармонических колебаний

При механических колебаниях колеблющееся тело (или материальная точка) обладает кинетической и потенциальной энергией. Кинетическая энергия тела W:

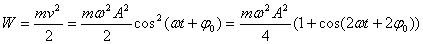
(Скорость тела v = ds/dt)

Для вычисления потенциальной энергии тела воспользуемся самой общей формулой, связывающей силу и потенциальную энергию тела в поле этой силы:

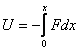
где U - потенциальная энергия, набираемая (или теряемая) телом, движущимся в силовом поле F от точки 0 (точки, в которой потенциальная энергия принимается равной 0) до точки х.

Для силы, линейно зависящей от смещения (как в случае наших механических маятников, такие силы носят общее название квазиупругих сил) мы имеем:

Сравнивая формулы

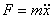
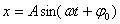
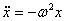
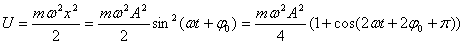
для кинетической и потенциальной энергии механического маятника, можно сделать следующие выводы:

Затухающие и вынужденные колебания

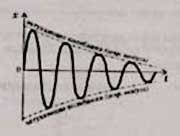
Затухающими называются колебания, энергия и амплитуда которых уменьшается с течением времени. Затухание свободных механических колебаний связано с убыванием механической энергии за счет действия сил сопротивления и трения.

ПРЕВРАЩЕНИЯ ЭНЕРГИИ ПРИ КОЛЕБАТЕЛЬНОМ ДВИЖЕНИИ

Колебания маятника возможны благодаря начальному запасу механической энергии, которая придается ему при выведении из положения равновесия.
При колебаниях маятника:
- в положении равновесия скорость и, следовательно, кинетическая энергия тела максимальны.
- потенциальная энергия маятника максимальна, когда кинетическая энергия (скорость) равна нулю.

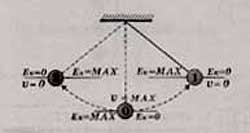
При движении маятника из положения равновесия в положение с максимальным смещением кинетическая энергия превращается в потенциальную энергию.
При перемещении из положения с максимальным смещением в положение равновесия потенциальная энергия переходит в кинетическую.

Если колебания свободные, т.е. трение отсутствует, то выполняется закон сохранения механической энергии: сумма кинетической и потенциальной энергий остается неизменной.

ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ

Вынужденными колебаниями называются незатухающие колебания системы, которые вызываются действием внешней периодической силы.

Сила, вызывающая вынужденные колебания, называется вынуждающей или возмущающей силой.

Принцип Гюйгенса — Френеля — основной постулат волновой теории, описывающий и объясняющий механизм распространения волн, в частности, световых.

Принцип Гюйгенса является развитием принципа, который ввёл Христиан Гюйгенс в 1678 году: каждая точка фронта (поверхности, достигнутой волной) является вторичным (т.е. новым) источником сферических волн. Огибающая фронтов волн всех вторичных источников становится фронтом волны в следующий момент времени.

Принцип Гюйгенса объясняет распространение волн, согласующееся с законами геометрической оптики, но не может объяснить явлений дифракции. Френель в 1815 году дополнил принцип Гюйгенса, введя представления о когерентности и интерференции элементарных волн, что позволило рассматривать на основе принципа Гюйгенса — Френеля и дифракционные явления.

Принцип Гюйгенса — Френеля формулируется следующим образом:

Каждый элемент волнового фронта можно рассматривать как центр вторичного возмущения, порождающего вторичные сферические волны, а результирующее световое поле в каждой точке пространства будет определяться интерференцией этих волн.

Густав Кирхгоф придал принципу Гюйгенса строгий математический вид, показав, что его можно считать приближенной формой теоремы, называемой интегральной теоремой Кирхгофа.

Фронтом волны точечного источника в однородном изотропном пространстве является сфера. Амплитуда возмущения во всех точках сферического фронта волны, распространяющейся от точечного источника, одинакова.

Дальнейшим обобщением и развитием принципа Гюйгенса является формулировка через интегралы по траекториям, служащая основой современной квантовой механики.

Абсолютный ноль

Абсолю́тный нуль температу́ры (реже^[1] — абсолютный ноль температуры) — минимальный предел температуры, которую может иметь физическое тело во Вселенной. Абсолютный нуль служит началом отсчёта абсолютной температурной шкалы, например, шкалы Кельвина. В 1954 году X Генеральная конференция по мерам и весам установила термодинамическую температурную шкалу с одной реперной точкой — тройной точкой воды, температура которой принята 273,16 К (точно), что соответствует 0,01 °C, так что по шкале Цельсия абсолютному нулю соответствует температура −273,15 °C^[2].

В рамках применимости термодинамики абсолютный нуль на практике недостижим. Его существование и положение на температурной шкале следует из экстраполяции наблюдаемых физических явлений, при этом такая экстраполяция показывает, что при абсолютном нуле энергия теплового движения молекул и атомов вещества должна быть равна нулю, то есть хаотическое движение частиц прекращается, и они образуют упорядоченную структуру, занимая чёткое положение в узлах кристаллической решётки (жидкий гелий составляет исключение). Однако, с точки зрения квантовой физики и при абсолютном нуле температуры существуют нулевые колебания, которые обусловлены квантовыми свойствами частиц и физического вакуума, их окружающего^[2].

В 1703 г. французский физик Гийом Амонтон (фр. Guillaume Amontons) представил воздушный термометр, в котором за нуль шкалы принималась температура, при которой воздух «теряет всю свою упругость». Рассчитанное им значение составило −239,5 °C.

В кинетической теории теплоты М. В. Ломоносова теплота объясняется «коловратным» движением. Прекращение движения означает предельную степень холода (по современной терминологии, абсолютный нуль).

В вышедшей в 1779 г. работе «Пирометрия» немецкий учёный Ламберт (нем. Johann Heinrich Lambert) уточнил полученное Амонтоном значение и получил −270 °C^[3].