Методические указания для преподавателей

ФИЗИЧЕСКАЯ КИНЕТИКА

для специальности 010701.65 Физика

Кемерово

СОГЛАСОВАНО:

СОГЛАСОВАНО:

Декан физического факультета

Проректор

по учебно-организационной работе

/Ф. В. Титов

/

А. А. Мить

( Ф.И.О. )

( Ф.И.О. )

от «

»

201___г.

от «

»

201___г.

УМК обсужден и одобрен на заседании Ученого совета физического факультета

УМК обсужден и одобрен научно-методическим советом КемГУ

Председатель Ученого совета

Председатель НМС

/ Ф. В. Титов

/

А. А. Мить

/ Ф.И.О. /

( Ф.И.О. )

Протокол №

Протокол №

от «

»

201___г.

от «

»

201___г.

ОБСУЖДЕНО:

РАССМОТРЕНО:

УМК обсужден и одобрен на заседании кафедры теоретической физики

УМК обсужден и одобрен методической комиссией физического факультета

Зав. кафедрой

Председатель методической комиссии

/А. С. Поплавной

/

/Н. И. Гордиенок

/

(Ф.И.О.)

(Ф.И.О. )

Протокол №

Протокол №

от «

»

января

201_3__г.

от «

»

201___г.

Содержание учебно-методического комплекса

№ п/п	компонент УМК	имя файла*	страницы
1.	Рабочая программа	РП Физкинетика.doc
2.	Методические указания для преподавателей
3.	Методические рекомендации для студентов
4.	Учебно-методические материалы
	– слайд-лекции	ФК Лекция 1 – ФК Лекция 12.ppt
	– сборник задач		6-43
5.	Контрольно-измерительные материалы		44-45
6.	Персоналии		46-57

Учебно-методические материалы

Опорным учебно-методическим материалом являются слайд-лекции.

Для практических занятий подобраны задачи, фрагмент которых представлен ниже.

Занятие №1

ТЕМА: Флуктуации

Задачи

1.1. Исследовать флуктуации энтропии и давления в паров ртути, если среднее значение температуры равно 2000 К, а среднее значение давления 0,01 мбар.

Решение.1.1. Согласно формулам и , приращение энергии Гиббса подсистемы и изменение энтропии системы как целого связанны соотношением

, (1)

где , , - флуктуации величин, относящихся к рассматриваемой подсистеме, а 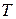и - средние равновесные значения температуры и давления для системы в целом. Отсюда для статистического веса получаем выражение

. (2)

Флуктуацию внутренней энергии можно разложить в ряд

. (3)

Первый закон термодинамики гласит

. (4)

Отсюда имеем

, . (5)

Подставляя соотношения (5) в (3), получаем

. (6)

На основании первого из соотношений (5) можно записать

, (7)

А на основании второго имеем

. (8)

Тогда из (6) находим

. (9)

С помощью (2) и (9) получаем

. (10)

Флуктуации не являются независимыми друг от друга. Флуктуации и 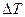можно записать в виде

, (11)

так что независимыми остаются только флуктуации и . Преобразуем показатель экспоненты выражения (10) в соответствии с (11)

. (12)

Рассмотрим дифференциал энтальпии

, (13)

из которого вытекает соотношение

. (14)

Поэтому в (12) смешанные члены с сокращаются. В формуле все величины отнесены к 1 кмоль. Если принять во внимание, что соотношение (12) относится к числу киломолей n, которое еще подлежит определению, то вместо следует написать

, (15)

где молярная теплоемкость, т.е. теплоемкость, отнесенная к 1 кмолю.

Подставляя (12) в (10) и учитывая (15), получаем

. (16)

Плотность вероятности

отвечает нормальному закону распределения с дисперсией

. (17)

Из сравнения (16) и (17) следует, что средний квадрат флуктуации энтропии равен

. (18)

Путем сравнения с распределением Гаусса при учете уравнения адиабаты и уравнения состояния идеального газа получаем для среднего квадрата флуктуации давления

, (19)

где среднее число частиц в рассматриваемом объеме 1 .

Таким образом, отклонения от средних значений весьма незначительны, несмотря на высокую плотность паров и малую величину объема (1 ), для которого эти отклонения определяются.

1.2. Определить относительную флуктуацию температуры при средней температуре и давлении мбар в объеме, равном 1 . Какова при указанных условиях относительная флуктуация объема для числа частиц, содержащегося в среднем в объеме, равном 1 ?

Решение.1.2. Статистический вес флуктуации определяется выражением

. (1)

Флуктуацию энтропии и флуктуацию давления запишется в виде

, (2)

Из дифференциала свободной энергии с учетом первого закона термодинамики получаем

, (3)

откуда

, . (4)

Следовательно,

. (5)

Далее, на основании имеем

;

при этом необходимо учитывать, что энтропия относительно только к рассматриваемому веществу.

Подставляя два последних выражения в первую из формул (2), находим

. (6)

Следовательно,

. (7)

Тогда статистический вес флуктуации , согласно (1), равен

. (8)

Из сравнения с плотностью вероятности нормального распределения

(9)

находим средние квадраты флуктуаций объема и температуры:

, . (10)

Отсюда при учете уравнения состояния идеального газа получаем относительную флуктуацию объема

, (11)

а для относительной флуктуации температуры с учетом закона равнораспределения имеем

. (12)

В соответствии с этим относительные флуктуации зависят только от числа частиц. Они тем меньше, чем больше частиц содержится в рассматриваемой части системы.

Поскольку при заданной температуре 300 колебания в молекуле кислорода еще не возбуждены, при численных расчетах молярную изохорную теплоемкость следует положить равной . Среднее число частиц находим по формуле

.

Подставляя это в (11) в (12), получаем

, .

Относительно большие флуктуации объясняются низким давлением и малостью рассматриваемого объема.

1.3. Найти флуктуацию числа частиц в 1 при нормальных условиях ( ).

Решение.1.3. Согласно формуле (10) из предыдущей задачи, средняя флуктуация квадрата объема равна

. (1)

Представим себе мысленно, что рассматриваемый объем отделен от остальной системы упругой перегородкой, и обозначим через N число частиц в этой замкнутой системе. Произведя деление, получаем из (1)

. (2)

При таком способе записи уже больше нельзя определить, какая из величин N и V поддерживается постоянной, а какая варьируется. Если теперь рассматривать число частиц в незамкнутом объеме, то можно представить (2)

в виде

.

Пользуясь уравнением идеального газа и учитывая соотношения 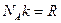, , получаем

. (3)

Следовательно, искомая флуктуация равна

, (4)

Откуда для средней относительной флуктуации имеем

. (5)

Таким образом, флуктуация числа частиц равна корню квадратному из числа частиц, а относительная флуктуация числа частиц равна величине, обратной корню из этого числа.

согласно (4), равна

.

Относительную флуктуацию находим из (5):

.

Задача 1.4.Наблюдаются флуктуационные колебания подвешенного зеркальца, имеющего момент инерции . Температура равна 300 К, измерение периода собственных колебаний дает величину . По кривой записи временной зависимости угла отклонения определено среднеквадратичное отклонение . Исходя из этого, вычислить постоянную Больцмана k и число Авогадро .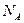

Рис.1. Флуктуации угла поворота вращающегося зеркала около нулевого положения.

Решение. 1.4. Для отклонения зеркальца на угол 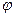необходим крутящий момент

, (1)

Где D – жесткость на кручение. Записывая уравнение движения для крутящего момента

(2)

и подставляя его в (1), приходим к дифференциальному уравнению

. (3)

Решение этого уравнения имеет вид

. (4)

Частота собственных колебаний равна

, (5)

Откуда для жесткости на кручение получаем выражение

(6)

(рис.1).

Определим теперь энергию, необходимую для отклонения зеркальца на угол 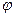. С помощью формулы

(7)

Находим потенциальную энергию крутильных колебаний:

. (8)

Отсюда на основании закона распределения Гиббса определяем статистический вес флуктуационного отклонения:

. (9)

Из сравнения с распределением Гаусса получаем

. (10)

В соответствии с этим постоянную Больцмана k можно найти путем измерения величин и Т:

, (11)

Подставляя в эту формулу измеренные значения, получаем

. (12)

С помощью этой величины находим число Авогадро

. (13)

Задача 1.5. Опредеделить среднее значение , где - постоянная, а - флуктуирующие величины, подчиняющиеся гауссовому распределению

.

Решение1.4. Требуется вычислить интеграл

.

Преобразованием показатель подынтегральной экспоненты приводится к виду

,

после чего интегрирование дает

.

Согласно соотношению имеем и затем . Таким образом, с учетом выражения имеем окончательно

.

Задача 1.6. Найти средний квадрат флуктуации энергии (пользуясь в качестве независимых переменных и ).

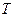Решение1.6. Имеем

Возводя в квадрат и усредняя, получим

Задача 1.7.. Найти (пользуясь переменными и ).

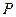Решение1.7.

Задача 1.8.Найти (пользуясь переменными ).

Решение1.8.

.

Задача 1.9. Найти (пользуясь переменными ).

Решение1.9.

Задача 1.10. Найти (пользуясь переменными ).

Решение 1.10.

Задача 1.11. Найти (пользуясь переменными ).

Решение 1.11.

Задача 1.12. Найти средний квадрат флуктуационного отклонения вертикально висящего математического маятника.

Решение 1.12. Пусть - длина маятника - его масса, 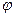- угол отклонения от вертикали. Работа в данном случае есть просто механическая работа против силы тяжести при отклонении маятника; для малых :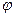

Отсюда

Задача 1.13. Найти средний квадрат флуктуационного отклонения точек натянутой струны.

Решение 1.13. Пусть - длина струны, 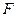- сила ее натяжения. Рассмотрим точку, находящуюся на расстоянии от одного из концов струны, и пусть - ее поперечное смещение. Для определения мы должны рассмотреть равновесную форму струны при заданном смещении у точки ; она состоит из двух прямых отрезков, проведенных из точек закрепления струны в точку . Работа, затрачиваемая при такой деформации струны, равна

.

Отсюда находим для среднего квадрата

.

Задача 1.14. Определить среднее значение произведения флуктуационных смещений двух различных точек струны.

Решение 1.14. Пусть - поперечные смешения точек, находящихся на расстояниях от одного из концов струны (причем ). Равновесная форма при заданных и составляется из трех прямых отрезков, и работа

.

По формуле найдем

.

Задача 1.15.Определить средний квадрат флуктуации числа частиц для электронного газа при температурах, малых по сравнению с температурой вырождения.

Решение 1.15. При вычислении можно пользоваться выражением для граничной энергии для при абсолютном нуле. Простое вычисление дает

.

Задача 1.16.Определить средний квадрат Фурье–компонент (с малыми волновыми векторами: ) флуктуации плотности в ферми – газе при .

Решение 1.16. Подынтегральное выражение в формуле

отлично от нуля (и равно единице) лишь в точках, в которых , , т.е. в точках принадлежащих сфере радиуса и в то же время не принадлежащих сфере того же радиуса с центром, сдвинутым на . Вычисляя объем этой области при , получим

.

Задача 1.17. Найти первую флуктуационную поправку к теплопроводности в области применимости теории Ландау.

Решение 1.17. Произведем вычисления для симметричной фазы в отсутствии поля. В первом приближении эффективный гамильтониан дается выражением

.

Вычисление статистического интеграла по формуле

дает

(интегрирование производится по половине пространства, поскольку и не зависимы). Представляя собой малую поправку в потенциале , это выражение дает поправку также и к потенциалу . Двукратное дифференцирование этого выражения по дает поправку к теплоемкости

(1).

Потребовав малости этой поправки по сравнению со скачком теплоемкости

,

мы снова придем к условию применимости теории Ландау в виде

.

Обратим внимание на большой численный коэффициент в знаменателе выражения в правой части неравенства.

Задачи для самостоятельного решения

1.Рассматривается водород при температуре 600 К и давлении . Найти средние флуктуации температуры, давления и энтропии, отнесенные к объему .

2. Чему равна средняя флуктуация энергии Гиббса для гелия при давлении и температуре 300 К?

3. Вычислить среднее число частиц в для идеального газа при температуре 500 К и давлении 1 мбар. Чему равна флуктуация числа частиц для этого объема?

4. При каком давлении идеального одноатомного газас температурой 300 К средняя флуктуация давления в объеме будет составлять 1% от общего значения?

5. В воды растворено 0,1 мг некоторого вещества с относительной молекулярной массой . Из раствора берутся пробы объемом 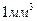каждая. Чему равна относительная флуктуация содержания вещества в пробе? Определить относительную долю проб с содержанием вещества более 0.01% среднего количества. Найти относительную флуктуацию давления раствора при 300 К.

6. 0,001 мг ртути испаряется в объеме 1 л . Чему равна средняя флуктуация парциального давления ртути при температуре 300 К , отнесенная к объему 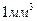? Чему равна относительная флуктуация? Относительная атомная масса ртути равна 200,6.

7. Вычислить отнесенную к объему 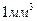флуктуацию внутренней энергии для гелия при температуре 1000 К и давлении мбар.

8. Чему равна средняя величина флуктуационного отклонения математического маятника, находящегося в поле земного тяготения ( ). Длинна маятника 2 см, масса 20 мг. Температура 300 К.

9. Чему равен коэффициент жесткости пружины D, если величина среднеквадратичного флуктуационного отклонения x составляет 1мм? Температура равна 500 К.

10. Определить предел чувствительности гальванометра с внутреннем сопротивлением R = 10 кОм, полное отклонение которого достигается за t = 5с в апериодическом режиме. 87,5 % подводимой электрической энергии превращаются за время успокоения в тепло. Температуру принять равной 300 К. Предполагается, что тепловые флуктуации подчиняются нормальному закону распределения и что вероятность ошибки при измерении не превышает 0, 27%.

11. Чему равны флуктуации компонент скорости в декартовой системе координат для водорода при 300 К?

Занятие №2

ТЕМА: Корреляции

Задачи

Задача 1. Найти коэффициент корреляции флуктуаций температуры и объема и коэффициент корреляции флуктуаций температуры и давления для гелия при нормальных условиях.

Решение. Искомые коэффициенты корреляции равны

, . (1)

. (2)

Подставляя сюда термодинамическую вероятность, согласно ,

получаем

~ . (3)

Этот интеграл можно разложить на два сомножителя, каждый из которых можно интегрировать независимо от другого:

~ . (4)

Первый интеграл дает среднее значение флуктуации объема, второй – среднее значение флуктуации температуры. Оба эти средние значения должны превращаться в нуль. Следовательно,

. (5)

Что касается средних квадратов флуктуаций и , то они в соответствии с формулами , отличны от нуля. Поэтому искомый коэффициент корреляции равен

. (6)

Таким образом, флуктуации температуры и объема не коррелированны. Для вычисления коэффициента корреляции воспользуемся соотношением

(7)

и получим

. (8)

Первое слагаемое обращается в нуль вследствие вытекающей из (5) некоррелированности флуктуаций объема и температуры. Средние квадраты флуктуаций температуры и давления определяются формулами

, .

С учетом этого находим из (8)

, (9)

Откуда следует, что коэффициент корреляции флуктуаций температуры и давления равны

. (10)

Следовательно, корреляция этих флуктуаций зависит от удельной теплоемкости, т.е. от числа степеней свободы рассматриваемого газа. Для одноатомных газов, согласно закону распределения, имеем , откуда для коэффициента корреляции флуктуаций температуры и давления получаем

. (11)

Таким образом, указанные флуктуации связанны весьма сильной корреляционной зависимостью.

Задача 2. Определить первый член разложения корреляционной функции разреженного газа по степеням .

Решение. Исходим из формулы

.

В первом приближении можно считать, что все остальные частицы, кроме двух заданных, находятся вдали друг от друга и их взаимодействием можно пренебречь, так что интегрирования дают . С той же точностью можно положить . В результате находим

,

Где - энергия взаимодействия двух частиц газа. Отметим, что подстановка этого выражения в формулу

.

дает для энергии газа

.

Этот результат находится, конечно, в соответствии с формулами

и

для свободной энергии слабо неидеального газа.

Задача 3. Определить средний квадрат Фурье–компонент (с малыми волновыми векторами: ) флуктуации плотности в ферми – газе при .

Решение. Подынтегральное выражение в формуле

отлично от нуля (и равно единице) лишь в точках, в которых , , т.е. в точках принадлежащих сфере радиуса и в то же время не принадлежащих сфере того же радиуса с центром, сдвинутым на . Вычисляя объем этой области при , получим

.

Задача 4. Определить корреляционную функцию для ферми–газа при температурах, низких по сравнению с температурой вырождения.

Решение. В интеграле в формуле

Полагаем и преобразуем его следующим образом:

.

Производим интегрирование по частям, после чего вводим новую переменную .

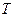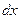Ввиду малости подынтегральное выражение быстро убывает с ростом , и потому интеграл по можно распространить от до :

,

где . Получившийся интеграл подстановкой приводит к В-интегралу Эйлера, и в результате получается

Для расстояний , усреднив быстро меняющийся квадрат косинуса, получаем окончательно

.

При эта формула переходит в

.

В асимптотической области, где велико не только по сравнению с 1, но и по сравнению с , имеем

.

Задача 5. Определить корреляционную функцию бозе-газа при .

Решение. При конечная доля числа частиц находится в состояниях с (конденсат). Возвращаясь к выражению

находим

, , где , причем дается формулой распределения Бозе с :

.

На расстояниях интеграл , так что

;

вторым членом можем пренебречь, если только 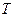не слишком близко к 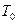(так что не слишком мало). В обратном случае, на расстояниях , интеграл

так что

.

Отметим, что привело бы к бесконечному значению флуктуации числа частиц.

Задача 6. Определить корреляционную функцию для бозе-газа на больших расстояниях ( ) при температурах выше точки 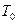начала бозе-эйнштейновской конденсации, но близких к ней.

Решение. Вблизи точки 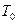химический потенциал мал. При этом интеграл в формуле

(обозначим его 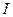) определяется областью малых значений :

~ ~ .

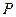Поэтому, разлагая подынтегральное выражение по 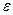и , находим

.

Окончательно получаем

.

Задача 7. Определить корреляционный радиус флуктуаций параметра по