Отношение порядка и отношение эквивалентности на графе.

Из указанных выше свойств очевидно, что граф даёт удобное геометрическое представление отношений на множестве, поэтому теория графов и теория отношений на множестве взаимно дополняют друг друга.

Будем считать, что на графе G=(X,Г) введено отношение порядка, если для любых 2-х вершин (х и у), удовлетворяющих условию х£у, $ путь из х в у. В этом случае говорят, что вершина х предшествует вершине у или что вершина у следует за вершиной х.

Покажем, что данное определение отражает на графе все свойства отношения порядка

Рефлексивность: Условие х£х истинно означает эквивалентность вершины самой себе, т.е. условие хºх. Однако при желании это условие можно рассматривать как наличие пути из х в х, т.е. как петлю в вершине х (рис. 2.8 а).

Транзитивность: Условие х£у, у£z ®х£z означает, что вершины x,y,z последовательно встречаются на одном и том же пути (рис. 2.8).

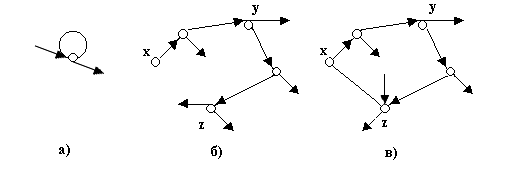
Рис.2.8 - Транзитивность на графах

Антисиметричность: Покажем справедливость условия х£у, у£х ®хºу. Левая часть этого выражения говорит о том, что существует путь из х в у, а так же существует путь из у в х. Но это означает, что в графе имеется контур, на котором лежат вершины х, у (рис. в).

Из правой части условия вытекает, что вершины, лежащие на одном и том же контуре, являются эквивалентными. Будем рассматривать этот вывод как определение эквивалентности на графе и покажем, что такое определение удовлетворяет всем трём условиям отношения эквивалентности. Условия рефлексивности хºх и симметрии хºу®уºх являются очевидными и вытекают из данного выше определения эквивалентности. Условие транзитивности хºy, yºz®xºz также является очевидным, так как говорит о том, что если в графе имеется контур с вершинами X и Y, а также контур с вершинами у и z , то имеется и контур, на котором лежат вершины х и z (рис. в).

Таким образом, отношение порядка совместно с отношением эквивалентности определяет некоторый граф.

На графе может быть также введено отношение строгого порядка. В этом случае для любых двух вершин (X и Y), удовлетворяющих условно X<Y, существует путь, идущий из X в Y. Условие транзитивности X<Y<Z®X<Z означает, как и в предыдущем случае, что вершины X, Y и Z встречаются последовательно на одном и том же пути. Условие антирефлексивности (X<X ложно) говорит об отсутствии петель на графе, а условие несимметричности (X<Y, у<õ взаимоисключается ) говорит об контуров.

Таким образом, отношение строгого порядка определяет граф без контуров.

Сведем все данные по отношениям порядка в таблицу 2.1.

Таблица 2.1 - Определение различных видов порядка

Порядки	Отношение
Антисимметричное	Транзитивное	Рефлексивное	Антирефлексивное	Полное	Неполное
Строгий	+	+		+
Нестрогий	+	+	+
Полный	+	+			+
Неполный	+	+				+

Характеристики графов.

Решение многих технических задач методами теории графов сводится к определению тех или иных характеристик графов, хотя технические приложения теории графов рассматривать в настоящей книге невозможно, знакомство с важнейшими характеристиками графов может оказаться полезным при изучении других дисциплин.

Цикломатическое число. Пусть G - неориентированный граф, имеющий n вершин, m рёбер и r компонент связности. Цикломатическим числом графа G называют число n(G)=m-n+r.

Это число имеет интересный физический смысл. Оно равно наибольшему числу независимых циклов в графе. При расчёте электрических цепей цикломатическим числом можно пользоваться для определения числа независимых контуров.

Хроматическое число. Пусть р- натуральное число. Граф G называют р-хроматическим, если его вершины можно раскрасить р различными цветами так, чтобы никакие две смежные вершины не были раскрашены одинаково. Наименьшее число р, при котором граф является р-хроматическим, называют хроматическим числом графа и обозначают y(G).

Если y(G)=2, то граф называют называют бихроматическим. Необходимым и достаточным условием того, чтобы граф был бихроматическим, является отсутствие в нём циклов нечётной длины. Хроматическое число играет важную при решении задачи наиболее экономического использования ячеек памяти при программировании. Однако его определение, за исключением случая бихроматического графа, представляет собой довольно трудную задачу, требующую нередко применения электронных вычислительных машин.

Пусть G – связный неориентированный граф, V и V – любые две его вершины. Тогда существует связывающая их простая цепь. М (L1,L2,…,Lq). Если количество ребер q этой цепи не минимальное из возможных , то существует цепь M( L1,L2,…,Lq) , связывающая U и U и имеющая меньшее число ребер. Т.о. существует связывающая U и U цепь М с минимальным количеством ребер р. Минимальная длина простой цепи с началом U и концом U называется расстояние d (U U) между этими вершинами.

Расстояние d(U’ U”) удовлетворяет аксиомам метрики.

1) d(U’ U”) >0 при цепи d(U’ U”) = 0 если U’= U”

2) d(U’ U”) = d (U’ U”)

3) Справедливо неравенство треугольника d(U’ U”)+d(U’ U”) >d(U’ U”).

Диаметр графа

d(G) = max d (U’ U”); U’, U” Î G (2.6)

Пусть V – произвольная вершина графа G. Максимальным удалением в графе G от вершины U называется величина (U) = max d(U U’) U’ G

Вершина U называется центром графа, если максимальное удаление от нее принимает минимальное значение

P (G) = min p (U’), U’ Î G (2.7)

Максимальное удаление р (G) от центра называется радиусом графа.

Центр не обязательно должен быть единственным.

Например в полном неориентированном графе, в котором любые две различные вершины U’ U” V соединены ребром, радиус равен 1 и любая вершина U V является центром.

Связный граф- все его вершины связаны между собой.