Отношение ЭКВИВАЛЕНТНОСТИ
Определение 1. Отношение, обладающее свойствами рефлексивности, симметричности и транзитивности называется отношением эквивалентности.
Комментарий.Это, например, отношение “равенства” чисел, или отношение “учиться в одной студенческой группе”, или отношение изоморфизма. Это определение избыточно потому, что любое симметричное и транзитивное отношение 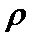 рефлексивно. В самом деле, пусть
рефлексивно. В самом деле, пусть 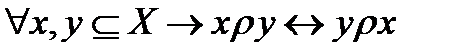 (в силу симметричности). Тогда, в силу транзитивности, имеет место
(в силу симметричности). Тогда, в силу транзитивности, имеет место 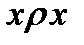 .
.
Теорема 1. Отношение эквивалентности разбивает множество на непересекающиеся подмножества  классы эквивалентности.
классы эквивалентности.

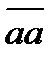 Пусть
Пусть  и
и  . То есть
. То есть  . Тогда
. Тогда 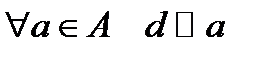 и
и 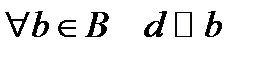 . Отсюда в силу транзитивности
. Отсюда в силу транзитивности 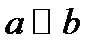 , но тогда
, но тогда 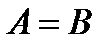 .■
.■
Определение 2. Множество классов эквивалентности данного множества называется фактор-множеством, а операция построения фактор - множества называется факторизацией.
Отношения ПОРЯДКА
Комментарий. Понятия порядка в математике нет, как нет понятия снега в языке чукчей. Это всегда какой-то, вполне определённый порядок.
Определение 1. Отношение, обладающее свойствами асимметричности, антирефлексивности и транзитивности называется отношением строгого порядка.
Комментарий.Например, “быть больше” на множестве чисел, “быть после” в очереди, “быть старше”. Это определение избыточно потому, что асимметричность можно показать, но удобно. В самом деле, пусть асимметричность не имеет место, то есть 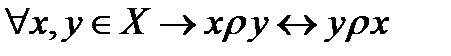 . Тогда из транзитивности имеет место
. Тогда из транзитивности имеет место 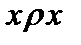 , что противоречит антирефлексивности.
, что противоречит антирефлексивности.
Определение 2. Если отношение антисимметрично, рефлексивно и транзитивно, то порядок называют нестрогим, а часто просто порядком.Например, «быть не выше».
Определение 3. Если строгий порядок обладают свойством полноты, то есть для любой пары несовпадающих элементов 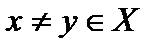 имеет место или
имеет место или 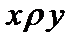 , или
, или 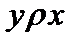 , то есть, нет несравнимых элементов, то его называют совершеннымилилинейным,а отношение
, то есть, нет несравнимых элементов, то его называют совершеннымилилинейным,а отношение 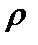 порождает структурусовершенного строгого порядка.
порождает структурусовершенного строгого порядка.
Определение 4. Если нестрогий порядок обладают свойством полноты, то есть для любой пары элементов 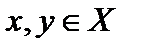 имеет место или
имеет место или 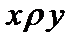 , или
, или 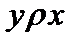 , то есть, нет несравнимых элементов, то его называют совершеннымилилинейным, а отношение
, то есть, нет несравнимых элементов, то его называют совершеннымилилинейным, а отношение 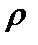 порождает структурусовершенного нестрогого порядка.Порядок называется частичным,если есть несравнимые элементы.
порождает структурусовершенного нестрогого порядка.Порядок называется частичным,если есть несравнимые элементы.
Определение 5. Множество 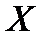 , структурированное отношением
, структурированное отношением 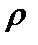 с совершенным порядком, называется совершенно упорядоченным(частично или строго).
с совершенным порядком, называется совершенно упорядоченным(частично или строго).
Пример. Пусть 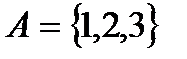 , тогда
, тогда 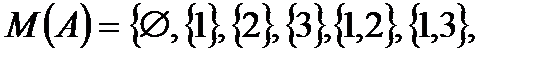
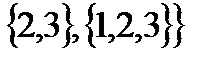 . Введём на множестве
. Введём на множестве 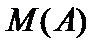 отношение строгого включения
отношение строгого включения 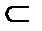 . Очевидно, что на множестве
. Очевидно, что на множестве 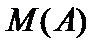 существуют несравнимые элементы, например
существуют несравнимые элементы, например 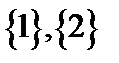 , то есть отношение
, то есть отношение 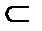 не порождает структурусовершенного строгого порядка.
не порождает структурусовершенного строгого порядка.
Определение 6. Элемент 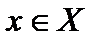 называется мажорантой множества
называется мажорантой множества 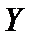 , если
, если 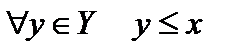 , а множество
, а множество 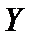 называют ограниченным сверху. Аналогично вводятся миноранта и ограниченное снизу множество.
называют ограниченным сверху. Аналогично вводятся миноранта и ограниченное снизу множество.
Определение 7. Миноранта всех мажорант множества 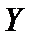 (если такая существует), называется супремумом множества
(если такая существует), называется супремумом множества 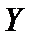 и обозначается
и обозначается 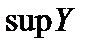 . Если
. Если 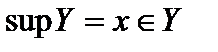 , то он называется наибольшим элементом множества
, то он называется наибольшим элементом множества 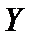 .
.
Аналогично вводятся нижняя грань 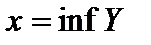 , множества
, множества 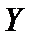 и наименьший элемент множества
и наименьший элемент множества 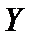 .
.
Определение 8. Если множество линейно упорядочено, и, кроме того, в любом его подмножестве можно выделить наименьший элемент, то оно называется вполне упорядоченным.
Определение 9. Любой класс эквивалентности вполне упорядоченных множеств по отношению "изоморфно" называют ординалом.
Пример. Множество натуральных чисел, любая последовательность, любое конечное линейно упорядоченное множество. Множество действительных чисел отрезка [0,1] при естественном способе упорядочения является линейно упорядоченным, но не является вполне упорядоченным, так как не всякое его подмножество имеет наименьший элемент, например, подмножество (0,1].
Бесконечные множества
Бесконечность  это именно то место, где
это именно то место, где
происходит всё то, чего не может быть.
Алекс Алдер.
Определение 1. Множества A и B называются эквивалентными или равномощными, если существует хоть одна биекция f: 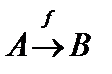 , то есть отношение равномощности есть отношение эквивалентности.
, то есть отношение равномощности есть отношение эквивалентности.
Комментарий. В качестве эталона можно использовать любоевполне упорядоченное множество, но общепринято использование натурального ряда чисел.
Определение 2. Множество, допускающее биекцию с любым куском натурального ряда чисел 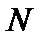 , называется конечным. Число элементов
, называется конечным. Число элементов 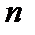 в конечном множестве А называют его мощностью.
в конечном множестве А называют его мощностью. 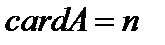 .
.
Определение 3. Множество, допускающее биекцию со всем натуральным рядом чисел 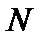 называется счетным. Мощность счетного множества
называется счетным. Мощность счетного множества 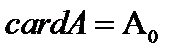 называется алеф ноль.
называется алеф ноль.
Определение 3. Кардиналами  называются классы эквивалентности множеств по отношению "равномощно".
называются классы эквивалентности множеств по отношению "равномощно".
Примеры. Множество целых чисел, множество чётных чисел, множество рациональных чисел, множество чисел вида 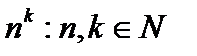 , и так далее. Ряд натуральных чисел можно поставить во взаимно однозначное соответствие с рядами квадратов натуральных чисел, степеней двойки, факториалов и т. п.:
, и так далее. Ряд натуральных чисел можно поставить во взаимно однозначное соответствие с рядами квадратов натуральных чисел, степеней двойки, факториалов и т. п.:
1 2 3 4 5 … 1 4 9 16 25 … 2 4 8 16 32 … 1 2 6 24 120
Комментарий. Данное рассуждение демонстрирует нарушение принципа “часть меньше целого” и лежит в основе парадокса Тристрама Шенди, предложенного Расселом в книге “Мистицизм и логика”. В романе Стерна “Жизнь и мнения Тристрама Шенди, джентльмена” герой обнаруживает, что ему потребовался целый год, чтобы изложить события первого дня его жизни, и еще один год понадобился, чтобы описать второй день. То есть материал его биографии накапливается быстрее, чем он сможет его обработать, и он никогда не сможет её завершить. Hо если бы он жил вечно, то события n-го дня Шенди мог бы описать за n-й год. Таким образом, он смог бы описать каждый день, а его жизнь насчитывала бы столько же лет, сколько дней.
Пример. Рассмотрим ещё один факт такого же рода. Построим бесконечное множество следующим образом: на каждом шаге в множество будем добавлять два элемента из натурального ряда, и после этого убирать первый в порядке следования. Получим следующую схему: {1, 2}; {2}; {2, 3, 4}; {3, 4}; {3, 4, 5, 6}; {4, 5, 6}… Возникает вопрос: сколько элементов будет в этом бесконечном множестве? Количество элементов возрастает. Но на первом шаге мы убрали из множества первый элемент, на втором шаге – второй и так далее. Если рассматривать каждый конкретно взятый элемент, то окажется, что его нет во множестве, то есть множество пустое.
Комментарий. Любое неконечное множество называется бесконечным.Очевидно, имеет место принцип Вейерштрасса: если бесконечное множество разбить на конечное число подмножеств, то по крайней мере одно из них будет бесконечно.
