Современная стоимость постоянной ренты постнумерандо
Под современной стоимостью потока платежей понимают сумму дисконтированных членов этого потока на некоторый предшествующий момент времени.
Годовая рента:
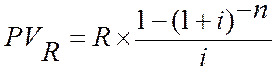 .
.
Множитель, на который умножается член ренты R, называется коэффициентом приведения ренты.
Пример: Годовая рента постумерандо характеризуется параметрами: R = 4 млн. руб., n = 5. При дисконтировании по сложной ставке процента, равной 18,5% годовых, получим:
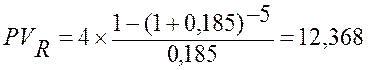 млн. руб.
млн. руб.
Таким образом, все будущие платежи оцениваются в настоящий момент в сумме 12,368 млн.руб. Иначе говоря, 12,368 млн. руб., размещенных под 18,5% годовых, обеспечивают ежегодную выплату 4 млн. руб. в течение 5 лет.
Годовая рента, начисление процентов m раз в году:
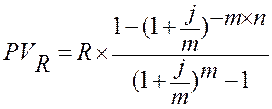 .
.
Рента p-срочная (m = 1):
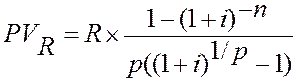 .
.
Рента p-срочная (p = m). Число членов ренты здесь равно числу начислений процентов; величина члена ренты составляет R/m:
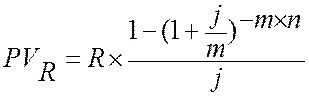 .
.
Рента p-срочная (p ≠ m).
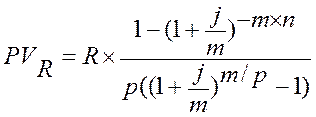 .
.
Рента с непрерывным начислением процентов.Пусть, как и выше, ряд состоит из ежегодных платежей, равных R, однако проценты начисляются непрерывно, сила роста равна δ.
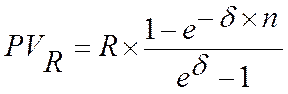 .
.
Если имеет место p-срочная рента с непрерывным начислением процентов, то:
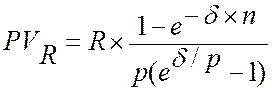 .
.
Консолидация задолженности
В практике возникают случаи, когда необходимо заменить одно обязательство другим, с более отдаленным сроком платежа, досрочно погасить задолженность, объединить несколько платежей в один (консолидировать платежи) и т.п. В таких случаях речь идет о финансовой эквивалентности обязательств, которая предполагает неизменность финансовых отношений сторон до и после изменения контракта.
Эквивалентными считаются такие платежи, которые после приведения их к одному моменту времени оказываются равными.
Метод решения подобного рода задач заключается в разработке уравнения эквивалентности. Одним из распространенных случаев изменения условий сделки является консолидация (объединение) платежей.
Рассмотрим это на примере.
Пусть платежи FV1, FV2, …, FVm со сроками n1, n2, …, nm заменяются одним в сумме FVo со сроком no. В этом случае возможны две постановки задачи:
1. Определение суммы консолидированного платежа FVo при заданном сроке no;
2. Определение срока консолидированного платежа no при заданной сумме FVo.
1. Определение суммы консолидированного платежа
При объединении обязательств можно применять простые и сложные процентные и учетные ставки. При этом все сроки приводится к одному no, с учетом, что часть из них больше (no<nk), а часть меньше консолидированного срока (no>nj). Формулы для определения суммы консолидированного платежа:
1.1 По простой процентной ставке:
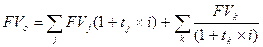 ,
,
где FVj – размеры объединяемых платежей со сроками nj<no;
tj=no-nj;
FVk – размеры объединяемых платежей со сроками nk>no;
tj=nk-no;
1.2 По сложной процентной ставке:
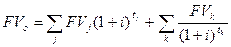 ,
,
1.3 По простой учетной ставке:
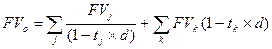 ,
,
Пример: Два платежа 1000 и 500 руб. со сроками уплаты 180 и 210 дней объединяются в один со сроком 200 дней. Ставка 20% годовых. Определить сумму консолидированного платежа, при использовании простой процентной ставки.
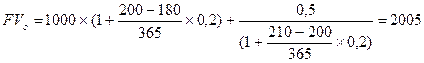 руб.
руб.
2. Определение срока консолидированного платежа
Если при объединении платежей задана величина консолидированного платежа FVo, то для определения срока no уравнение эквивалентности удобно представить в виде равенства современных стоимостей соответствующих платежей. В расчетах также применяются простые и сложные ставки.
Формулы для определения срока консолидированного платежа:
2.1 По простой процентной ставке:
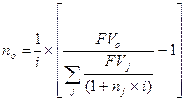 ,
,
2.2 По сложной процентной ставке:
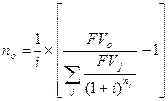 ,
,
2.3 По простой учетной ставке:
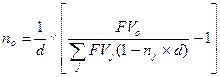 ,
,
Пример: Суммы в размере 800, 1000 и 200 руб. должны быть выплачены через 50, 70 и 120 дней соответственно. Определить срок консолидированного платежа в размере 600 руб. при использовании простой учетной ставки 10% годовых.
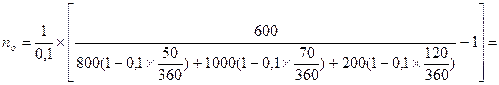 3,06 года
3,06 года
Эквивалентность ставок
Эквивалентные ставки – это ставки, в конкретных условиях сделки приводящие к одному и тому же результату.
Принцип эквивалентности ставок применяется при сравнении ставок, используемых в различных сделках и соглашениях, определении эффективности финансово-кредитной операции, безубыточной замене одного вида процентных ставок (или метода их начисления) другим.
Вывод формул эквивалентности ставок во всех случаях основывается на равенстве взятых попарно множителей наращения:
1) простая процентная и сложная процентная ставки:
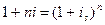 ,
,
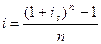 ,
,
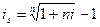 ,
,
где i – простая процентная ставка;
is – сложная процентная ставка;
n – срок .
2) простая процентная и простая учетная ставки:
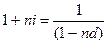 ,
,
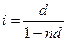 ,
,
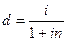 ,
,
где d – простая учетная ставка.
3) простая процентная и сложная учетная ставки:
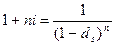 ,
,
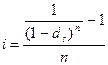 ,
,
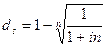 ,
,
где ds – сложная учетная ставка.
4) сложная процентная и простая учетная ставки:
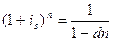 ,
,
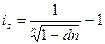 ,
,
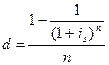 ,
,
5) сложная процентная и сложная учетная ставки:
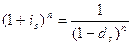 ,
,
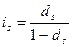 ,
,
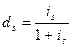 ,
,
6) простая учетная и сложная учетная ставки:
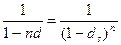 ,
,
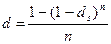
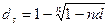 .
.
Пример: За 2 года до даты погашения вексель учтен по простой учетной ставке 20% годовых. Определить доходность учетной операции в виде сложной учетной ставки.
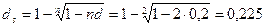 или 22,5%.
или 22,5%.
