Раздел 2. Задания для практических занятий

Задание 1. Ознакомиться с факторами, оказывающими влияние на необходимый размер капитала банка

При определении необходимого размера капитала банка следует в первую очередь учитывать минимально допустимый размер его капитала и нормативы, установленные регулирующими органами, при расчете которых используется величина собственных средств (капитала) банка. В Федеральном законе «О Центральном банке РФ» приведен перечень следующих нормативов:

1. Норматив достаточности капитала (коэффициент взвешенного риска)   2. Максимальный размер риска на одного или несколько заемщиков   3. Максимальный размер крупных кредитных рисков     4. Максимальный размер риска на одного кредитора (вкладчика)     5. Максимальный размер привлеченных денежных вкладов населения   6. Норматив использования собственных средств банков для приобретения долей (акций) других юридических лиц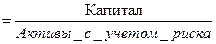

= Устанавливается в процентах от собственных средств кредитной организации с учетом всей суммы выданных кредитов (гарантии, поручительства и др.).   = Устанавливается как процентное соотно-шение совокупной величины крупных рисков и собственных средств кредитной организации (крупным кредитным риском считается объем кредитов, гарантии, поручительства в пользу одного клиента в размере свыше 5% собственных средств кредитной организации).   = Устанавливается как процентное соотношение величины вклада или полученного кредита, полученных гарантий и поручительств, а также остатков на счетах одного или связанных между собой кредиторов и собственных средств кредитной организации.   = Устанавливается как предельное соотношение общей суммы денежных вкладов (депозитов) граждан и величины собственных средств (капитала) банка. = Устанавливается как процентное соотношение размеров инвестируемых и собственных средств кредитных организаций, причем размер собственных средств для приобретения долей (акций) не должен превышать 25% собственных средств кредитной организации.

Задание 2. Освоить методику расчета дохода финансовых операций.

Доход от любой финансовой операции можно представить в виде:

Е = Р • r,

где Р - сумма вложенных средств; т - норма дохода на вложенный капитал (доходность операции).

Если в результате инвестирования суммы Р в течении срока (n) лет (n может быть < 1) получена сумма:

S = Р + Е,

где Е - полученный доход,

такую операцию можно представить в виде эквивалентной операции размещения той же суммы по соответствующим эквивалентным (эффективным) годовым ставкам.

Следовательно, эффективная ставка простых процентов будет равна:

i_э = r(K/t), (2.1)

где t - срок операции в днях;

К - расчетное количество дней в году.

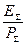При сравнении доходности видов операций банка и групп операций в каждом виде различной их детализации необходимо определять доходность некоторой совокупности операций. При этом, если известны общая сумма вложенных средств по совокупности операций 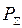за период t дней и полученный общий доход 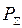, норма доходности вложенных средств будет равна:

r =

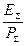а соответствующая годовая эквивалентная ставка по формуле (2.1) составит:

i_э = r(K/t)= (K/t)

Другим подходом к определению доходности совокупности финансовых операции является ее расчет как средневзвешенной доходности, которая определяется следующим образом:

iа = [(ia_l • P₁) + (ia₂ • Р₂) + ... + (ian • Рn)] / [Р₁ + Р₂ + ... + Рn], (2.2)

или

ia = ia_l(P_l / P) + ia₂(P₂ / P) + iаn(Рn / n),

где iak (k = 1,2,..., n) - доходность операции (группы операции) в виде годовой ставки процентов; Р - сумма вложенных средств: Р = P₁ + Р₂ + ... + Рn.

Если при размере работающих активов Ар регулирующие органы увеличили норму обязательного резервирования в Центральном банке для некоторых видов обязательств, вследствие чего банк должен дополнительно перечислить в эти резервы сумму, равную 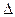Ар, уменьшив ее на величину размера работающих активов, то для обеспечения прежней величины дохода ему придется увеличить среднюю доходность работающих активов, равную i_a, (i_a= [Е / Acp][K/t], где Е - доход, полученный от активных операций банка за период t дней; Аср - средний остаток средств на соответствующих счетах активов, приносящих доход, К - расчетное количество дней в году), до величины i_ap, определяемой из соотношения:

Api_a = (Ар - 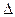Ар) i_ap и равной i_ap = [Ар / (Ар - 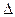Ар)] i_a (2.3)

Задание 3. Ознакомиться с операциями наращения и дисконтирования

Эффективность финансовой сделки (например, предоставление в долг некоторой суммы Р с условием, что через некоторое время будет возвращена сумма S) может быть охарактеризована одной из двух величин:

темп прироста r(t) = (S - Р) / Р, (2.2.1)

темп снижения d(t) = (S - Р) / S, (2.2.2)

В финансовых вычислениях первый показатель еще имеет название «процент», «рост», «ставка процента», «норма доходности», а второй - «дисконт», «ставка дисконтирования», Обе ставки взаимосвязаны:

r(t) = d(t)/(l - d(t)) или d(t) = r(t)/(l + r(t)).

Процесс, в котором заданы исходная сумма и процентная ставка - процесс наращения.

Процесс, в котором заданы возвращаемая сумма и коэффициент дисконтирования - процесс дисконтирования.

Экономический смысл финансовой сделки, задаваемый формулой (2.2.1), состоит в определении той суммы, которой будет или желает располагать инвестор по окончании этой операции. Поскольку из формулы (2.2.1)

S = P + P-r(t) и Р • r(t) > 0, то видно, что время генерирует деньги.

Экономический смысл дисконтирования заключается во временном упорядочении денежных потоков различных периодов. Коэффициент дисконтирования показывает, какой ежегодный процент возврата хочет (или может) иметь инвестор (вкладчик) на вложенный капитал. Величина Р показывает как бы текущую, «сегодняшнюю» стоимость будущей величины S.

Дисконт, связанный суммовыми величинами, (формула (2.2.2)), используется, главным образом, в операциях по учёту векселей банком. Схема действия такова. Владелец векселя на сумму S предъявляет его банку, который соглашается его учесть, т. е. купить, удерживая в свою пользу часть вексельной суммы, которая называется дисконтом. В этом случае банк предлагает владельцу сумму Р, исчисляемую исходя из объявленной банком ставки дисконтирования (d). Расчет суммы - есть следствие формулы (2.2.2):

P = S(l – f • d), (2.2.3)

где f - относительная длина периода до погашения векселя (операция имеет смысл, когда число в скобках не отрицательно).

Задание 4.Ознакомиться с понятиями простого и сложного процента

Простые проценты

В зависимости от способа начисления проценты делят на простые и сложные. При использовании простых процентов сумма процентов в течение всего срока долга определяется исходя из первоначальной суммы долга независимо от количества периодов начисления и их длительности. Сумма процентов при этом определяется по формуле:

J = n • J_r = n • i• P, (2.3)

J_r - сумма процентов за год,

Р - сумма, на которую начисляются проценты;

i – годовая ставка процентов в относительных единицах.

Если срок хранения вклада выражается в днях, то в формулу (2.3) следует подставить выражение n = t / К.

Сумма долга с начисленными процентами будет определять выражением:

S = P + J = P(1 + n • i) (2.4)

Эта формула может быть представлена в виде:

S = P • k_н (2.5)

где k_н - множитель (коэффициент) наращения.

Заметим, что увеличение процентной ставки или срока в (k) раз увеличит множитель наращения в (1 + kni)/(l + ni) раз.

В банковской практике различных стран срок в днях и расчетное количество дней в году при начислении процентов определяется по-разному. В так называемой германской (коммерческой) практике расчёт числа дней основывается на длительности года в 360 дней и месяцев в 30 дней; во французской - длительность года равна 360 дням, а количество дней в месяцах - равно их фактической календарной длительности (28, 29, 30, 31); в английской - длительность года равна 365 дням и соответствующая точная длительность месяцев.

При изменении суммы на счёте общая сумма процентов за весь срок хранения вклада будет равна сумме процентов, начисленных для каждого периода начисления, в котором сумма на счёте была постоянна. При этом в практике используется также методика расчета с вычислением так называемых процентных чисел, определяемых выражением:

Процентное число = (Сумма • Длительность в днях) / 100.

Для определения суммы начисленных процентов все процентные числа складываются и их сумма делится на постоянный делитель, вычисляемый следующим образом: Количество дней в году / Годовая ставка процентов. Объединяя данные выражения, получаем для одного период начисления: Проценты = (Сумма • Длительность в днях• Процентная ставка)/(100 • Количество дней в году) = Длительность в днях / Количество дней в году • Процентная ставка • Сумма /100.

Если ставки процентов изменяются в течение срока хранения вклада, сумму начисленных процентов можно определить, применяя последовательно формулу (2.3). Пусть на последовательных интервалах времени n₁ и n₂ используются простые ставки процентов i₁ и i₂, тогда по (2.3) сумма процентов, начисленных за первый интервал, будет равна:

J₁ =n₁ • i₁ • Р.

Сумма процентов, начисленных за второй интервал, составит:

J₂ =n₂ • i₂ • Р.

Общая сумма процентов за два интервала начисления будет равна:

J = J₁ + J₂ = n₁ • i₁ • Р + n₂ • i₂ • Р = P(n₁ • i₁ + n₂ • i₂)

Наращенная сумма за два интервала начисления составит:

S = P + J = Р(n₁ • i₁ + n₂ • i₂).

При N интервалах начисления, на каждом из которых будет применяться своя ставка процентов, сумма процентов составит:

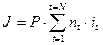(2.6)

Сумма вклада с процентами (наращенная сумма) будет в этом случае равна:

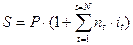(2.7)

Из формулы (2.4.) можно при прочих заданных условиях определить срок вклада в годах:

n = (S - P)/P • i (2.8)

или в днях:

t = ((S - P)/P • i)K, (2.9)

а также ставку простых процентов при прочих заданных условиях:

i = (S - P)/(P • t)K. (2.10)

Используя формулу (2.4.), можно определить сумму вклада при заданных значениях суммы вклада с начисленными процентами, срока вклада и ставки процентов:

P = S/(1 - n • i) = S/(1 + t/k). (2.11)

Это выражение можно также записать в виде:

P = S • k_d,

где k_d = 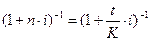- коэффициент дисконтирования (он, как видим величина множителя (коэффициента) наращения).

Сложные проценты

При начислении сложных процентов сумма процентов, начисленных после первого периода начисления, являющегося частью общего срока хранения вклада, не выплачивается, а присоединяется сумме вклада. База для начисления сложных процентов в отличие от использования простых процентов будет увеличиваться с каждым периодом начисления, являющимся частью общего срока хранения вклада.

Если проценты за период начисления начисляются по постоянной сложной старке in и все периоды начисления имеют одинаковую длительность, сумма вклада с процентами в конце первого периода по формуле (2.4) будет равна:

S₁=Р • (1+n • i).

Сумма вклада с процентами в конце второго периода составит:

S₂=S₁ • (1+n • i_n)=Р • (1+n • i)²

Если в течение срока хранения вклада будет N одинаковых периодов начисления, сумма вклада с процентами в конце срока составит:

S=Р • (1+ i)ⁿ. (2.12)

Сумма начисленных процентов будет равна:

J = S-P=P[(1 + n • i)^N - 1]. (2.13)

Если срок хранения вклада в годах (n) не является целым числом, множитель наращения можно определить двумя способами. При первом способе используют формулу (2.12) с соответствующим нецелым показателем степени. При втором способе множитель наращения определяется по выражению:

k_h = (1+ i)ⁿ¹ - (1+n₂ • i), (2.14)

где n₁ - целое число лет в течение срока вклада;

n₂ - оставшаяся дробная часть года.

При начислении сложных процентов несколько раз в году (месяцам, по кварталам, по полугодиям) сумма вклада с процента (наращенная сумма) при сроке (т) лет будет равна:

S=P(1 + n • i)^N= P(1 + j/m)^N (2.15)

где i_n - ставка за период начисления;

j - номинальная годовая ставка процентов;

m - количество периодов начисления в году;

N - количество периодов начисления в течение срока хранения вклада (N = n • m).

Сумма начисленных процентов составит:

J = P[(l+j/m)^N – 1 ]. (2.16)

Используя формулы для наращенной суммы при начислении сложных процентов один или несколько раз в году, можно получить выражение для срока хранения вклада при заданных прочих условиях. При использовании сложной годовой ставки процентов срок хранения в годах будет равен:

n = 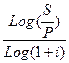(2.17)

Из формул для наращенной суммы можно также определить ставку сложных процентов при прочих заданных условиях:

i= 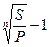(2.18)

При использовании годовой ставки сложных процентов(1) и сроке хранения (n) лет дисконтированное значение будущей суммы вклада с процентами будет равно:

P = S/(l+i)ⁿ=S • k_d, (2.19)

где k_d = 1/(1 + i)ⁿ - коэффициент дисконтирования (приведения).

При наличии сложных процентов несколько раз в году дисконтированная сумма будет равна:

P=S/(1+j/m)^N. (2.20)