Управление инвестиционным портфелем

Возможны следующие стратегии управления:

1. Активное (совершение частых операций на основе анализа меняющейся конъюнктуры рынка) и пассивное (приобретение бумаг на длительный срок и сохранение его практически в неизменном виде) управление

2. Управление личное и доверительное

3. На основе различных технологий управления и правил принятия решений о продаже или покупке ценных бумаг.

Главная проблема в формировании портфеля инвестиций состоит в обеспечении оптимального соотношения между риском и доходностью. Правило: чем более высокий доход приносит ценная бумага, тем больший потенциальный риск она имеет. Решается эта проблема, прежде всего на основе диверсификации портфеля (т.е. распределения средств между различными активами) и тщательного подбора фондовых инструментов.

Очевидно, что доходность портфеля ( dp ) представляет собой линейную функцию показателей доходности входящих в него активов и может быть рассчитана по формуле средней арифметической взвешенной (в данном случае речь может идти как об ожидаемой, так и о фактической доходности):

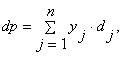(2.6.1)

где dj — доходность j -го актива;

yj — доля j -го актива в портфеле;

n — число видов активов в портфеле.

Следует помнить, что формирование портфеля из наиболее доходных активов в общем случае приводит к увеличению его риска.

Мерой риска портфеля, как и отдельного актива, служит вариабельность его доходности. Взаимосвязь между риском портфеля и риском входящих в него активов не описывается формулой средней арифметической. Как известно из курса статистики, в многомерном случае необходимо учитывать взаимосвязь значений доходности активов портфеля с помощью показателя ковариации и коэффициента корреляции.

В частности, если в качестве меры риска актива выступает среднее квадратическое отклонение, то его значение для портфеля, содержащего k видов активов, может быть найдено по формуле:

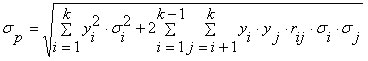(2.6.2)

где σ_p– мера риска портфеля;

y_i— доля i -го актива в портфеле;

σ_i— вариация доходности i -го актива;

r_ij— коэффициент корреляции между ожидаемыми доходностями i -го и j -го активов.

Для портфеля из двух активов эта формула существенно упрощается и имеет вид:

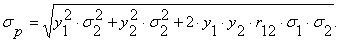(2.6.3)

Из приведенных формул следуют выводы:

1) риск, ассоциируемый с каким-то конкретным активом, не может рассматриваться изолированно от всего портфеля, т.е. любая новая инвестиция должна анализироваться с позиции ее влияния на изменение доходности и риска инвестиционного портфеля в целом;

2) если доходность портфеля равна средней доходности входящих в него активов, то риск портфеля может быть как больше, так и меньше среднего значения; при определенном сочетании активов можно добиться значительного снижения риска портфеля;

3) риск портфеля зависит не от значений доходности, а от их вариации; кроме этого риск портфеля зависит от количества активов в портфеле, структуры портфеля, рисковости и динамики доходности его составляющих.

4) разнонаправленность тенденций финансовых активов, приводящих к отрицательному значению коэффициента корреляции, способствует снижению риска портфеля (если портфель состоит из двух активов, связанных обратной функциональной зависимостью, то его риск равен нулю).

5) добавление в портфель безрискового актива уменьшает доходность портфеля, при этом риск портфеля уменьшается прямо пропорционально доле этого актива;

6) объединение рисковых активов в портфель может приводить к снижению риска по сравнению с обладанием каждым из этих активов в отдельности, однако результат зависит не только от рисковости объединяемых активов, но и от характера взаимосвязи между их доходностями. В общем случае риск комбинации активов меньше среднего риска объединяемых активов;

7) при объединении в портфель независимых активов (в этом случае значения парных коэффициентов корреляции равны нулю) риск портфеля находится как среднее взвешенное рисков отдельных активов, формирующих портфель:

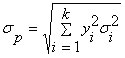(2.6.4)

8) если имеются на выбор два актива с одинаковыми характеристиками, однако доходность одного из них меняется однонаправленно, а доходность второго — разнонаправленно с доходностью портфеля, то с позиции минимизации риска для включения в портфель следует предпочесть второй актив.

При формировании портфеля теоретически могут ставиться три основные целевые задачи: 1) достижение максимально возможной доходности; 2) получение минимально возможного риска; 3) получение некоторого приемлемого соотношения «доходность/риск».

Первая задача решается путем формирования портфеля из одного наиболее доходного актива; вторая – из одного наименее рискового (безрискового) актива. В действительности смысл формирования портфеля состоит в поиске комбинации активов, обеспечивающей рост (неснижение) доходности при снижении (невозрастании) риска. Эта задача не имеет однозначного решения.

Модель оценки капитальных активов (capital asset pricing model – CAPM) впервые предложил Уильям Ф.Шарп (William F. Sharpe), получивший Нобелевскую премию по экономике за 1990г. В настоящее время это базисная теория современной финансовой науки и подробно рассматривается во всех курсах, связанных с рынком капитала.

САРМ определяет взаимосвязь между ожидаемой доходностью финансового актива и его риском. Основная идея правила оценки долгосрочных активов состоит в том, что ожидаемая премия за риск каждой ценной бумаги должна расти пропорционально ее «бете» - мере систематического риска.

Под рыночным портфелем (market portfolio) здесь понимается портфель, в котором доля каждой ценной бумаги пропорциональна ее доле в общей капитализации рынка.

Основные допущения:

1. Инвесторы производят оценку инвестиционных портфелей, основываясь на ожидаемых доходностях и их стандартных отклонениях за период владения.

2. Инвесторы никогда не бывают пресыщенными. При выборе между двумя портфелями они предпочтут тот, который, при прочих равных условиях, дает наибольшую ожидаемую доходность.

3. Инвесторы не желают рисковать. При выборе между двумя портфелями они предпочтут тот, который, при прочих равных условиях, имеет наименьшее стандартное отклонение.

4. Частные активы бесконечно делимы. При желании инвестор может купить часть акции.

5. Существует безрисковая процентная ставка, по которой инвестор может дать взаймы (т.е. инвестировать) или взять в долг денежные средства.

6. Налоги и операционные издержки несущественны.

7. Все инвесторы планируют свои действия на один, одинаковый для всех, период владения.

8. Безрисковая процентная ставка одинакова для всех инвесторов.

9. Информация свободно и незамедлительно доступна для всех инвесторов.

10. Все инвесторы одинаковым образом анализируют ценные бумаги и придерживаются одинаковых экономических воззрений на окружающий мир. Следовательно, все они приходят к одинаковым оценкам распределения вероятностей будущих денежных потоков в результате инвестирования в доступные для них ценные бумаги. Это означает, что при заданной совокупности цен финансовых активов и безрисковой процентной ставке все инвесторы пользуются для определения эффективной границы и уникального оптимального рискованного портфеля одними и теми же ожидаемыми ставками доходности, среднеквадратическими отклонениями и коэффициентами корреляции. Это предположение часто называют однородностью ожиданий (homogeneous expectations).

Математически формула определения ожидаемой ставки доходности на долгосрочный актив имеет следующий вид:

Ri = Rf + β(Rm-Rf)

где,
Rf - доходность безрисковых активов, под которой, как правило, понимают доходность государственных ценных бумаг;
Rm - ожидаемая средняя норма прибыли рыночного портфеля;
(Rm-Rf) - премия за риск вложения в акции (в ряде учебных пособий премия за рыночный риск принимается равной 5%);
β - коэффициент, характеризующий чувствительность оцениваемой ценной бумаги к изменениям рыночной доходности (рассчитывается по статистическим данным и выражает вариабельность доходности ценной бумаги по отношению к среднерыночной доходности).

Как видно из модели, ожидаемая доходность (Ri) акций компании является функцией трех взаимосвязанных и взаимообусловленных параметров: среднерыночной доходности; без рисковых вложений и присущего рассматриваемой компании β-коэффициента.

Среднерыночная доходность (Rm) представляет собой доходность рыночного портфеля. В качестве данного показателя берут, например, среднюю доходность по акциям, включенным в рыночный портфель, используемый для расчета какого-либо общеизвестного индекса (Индекс ММВБ, Nikkei 225 и т.п.), данные значения легко можно найти в открытом доступе.

Без рисковая доходность (Rf) представляет собой, ожидаемый среднегодовой темп прироста экономики в долгосрочной перспективе, но с поправкой на изменение краткосрочной ликвидности и инфляцию. Единого мнения в отношении значения показателя нет. Так, американские финансовые аналитики полагают, что в качестве доходности безрисковых активов следует брать доходность по казначейским обязательствам, но вот какие обязательства использовать-долго- или краткосрочные, – единства нет.

Разницу между среднерыночной нормой доходности акций и безрисковой ставкой (Rм - Rf) называют премией за риск вложения в акции (equity risk premium). Премию за риск вложения в акции, как правило, определяют на базе исторических данных о премиях за риск, опубликованных Ibbotson Associates. Обычно эта премия варьируется в диапазоне 3,5% - 6%.

Бета-коэффициент (β) является основным фактором, отражающим эффект взаимных корреляций доходности бумаг анализируемой компании с доходностью ценных бумаг, обращающихся на данном рынке.

Коэффициент выражает меру систематического риска для акций компании, он характеризует вариабельность ее доходности по отношению к среднерыночной доходности (т.е. к доходности рыночного портфеля). Величина коэффициента определяется на основе анализа ретроспективных данных соответствующими статистическими службами фирм, специализирующихся на рынке информационно-аналитических услуг, инвестиционными и консалтинговыми компаниями и публикуется в финансовых справочниках и периодических изданиях, анализирующих фондовые рынки. Значение β составляет около 1 (для рынка в среднем бета = 1).

Известны достаточно простые алгоритмы, позволяющие найти приблизительное значение бета-коэффициента для данной ценной бумаги. Пусть Kij - доходность акций i-й компании в j-м году, a Kmj - доходность на рынке в среднем (j = 1, 2, ..., n) за все анализируемые периоды. Если к рынку применима модель САРМ, то, как следует из модели, β-коэффициент представляет собой коэффициент эластичности, а его значение можно рассчитать как отношение приращения доходности акций i-й компании (ΔKij) к приращению среднерыночной доходности (ΔKmj):

β = ΔKij/ΔKmj

Так как данные для расчета CAPM базируются на процентных ставках номинированных в долларах США, то при использовании рублевых денежных потоков необходимо скорректировать полученную величину ставки дисконтирования по следующей формуле:

Rrur = (1 + Rusd) x (1 + Brur) / (1 + Busd) - 1

где,
Rrur - ставка дисконтирования, номинированная в рублях;
Rusd - ставка дисконтирования, номинированная в долларах США;
Brur - доходность по рублевым государственным облигациям России;
Busd - доходность по еврооблигациям России, номинированным в долларах США.[4]

Одним из основных преимуществ в применении модели является то что, модель CAРM позволяет учесть влияние внешних факторов, не зависящих от хода реализации проекта, – страновые и политические риски, ставки доходности (без рисковые, отраслевые и среднерыночные). При этом, правда, следует учитывать и ее недостатки, к которым можно отнести:

1. Имеет прямое отношение только к компаниям, которые являются открытыми акционерными обществами и, следовательно, их акциями торгуют на фондовых рынках.
2. Вызывает затруднения при определении, какие из вложений можно считать без рисковыми, применим только к компаниям, которые располагают достаточной статистикой для расчета своего коэффициента бета или имеют возможность найти компанию-аналог, чей коэффициент бета мог бы использоваться в расчетах.

При использовании в модели информации зарубежных фондовых рынков в ставке дисконта необходимо учитывать дополнительный риск, связанный с инвестированием средств в Россию (страновой риск). Уровень риска инвестирования в конкретную страну определяется крупнейшими информационно-аналитическими и рейтинговыми агентствами.

Capital Asset Pricing Model, САРМ – центральная концепция современной финансовой экономики. Эта модель дает представление о том, какое должно быть соотношение между риском вложения в актив и доходностью этого вложения. Эта формула нашла широкое применение в теории современного инвестиционного анализа в самых различных его областях: оценки прибыльности проектов, портфельных инвестиций, оценки предприятий.

Построение модели арбитражного ценообразования, используемая для определения стоимости ценных бумаг, сопряжено с субъективным отношением инвестора к влияющим факторам. Что бы сохранить все преимущества модели и попытаться учесть недостатки предложен универсальный алгоритм построения модели, а так же приведена его численная реализация.

Теория арбитражного ценообразования (АРТ) была предложена профессором Йельского университета С. Россом в 1976 г. и является альтернативной САРМ моделью общего равновесия на финансовом рынке. Главным предположением теории является то, что каждый инвестор стремится использовать возможность увеличения доходности своего портфеля без увеличения риска.
Модель APT в общем виде выглядит: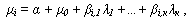

где 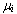средняя доходность i-го актива, 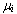доходность безрискового актива, 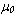- влияющие факторы риска.

Построение модели связано с определенным субъективизмом: какие факторы выбрать, какой должен быть критерий включения фактора в итоговую модель, все эти проблемы инвестор решает самостоятельно.

Автором был предложен алгоритм построения модели APT, в которой субъективный фактор сведен к минимуму.

Универсальный алгоритм построения 7 основных этапов:

1.Определение всей совокупности факторов возможно влияющих на цену, и разделение их, методом агрегирования, на группы.
Основными группами, по мнению автора, являются: финансовые показатели фирмы, макроэкономические индикаторы страны, отраслевые индикаторы, мировые фондовые индексы, сырьевые цены, политические и корпоративные события, и т.д.

2. Выделение для исследуемого предприятия аналоги, на основе: отраслевой принадлежности, ликвидности акций, капитализации, и т.д.

3.Анализ влияния каждой из групп на цену исследуемого актива и цены аналогов.

4. Сформированные новые группы проранжировать по уровню детерминации (R²) построенных моделей, который будет влиять на количество переменных в данных группах.

Ранжирование групп осуществляется по трем уровням:

· первый соответствует: 0,7 = <R² < 1 (установим, УГ = 1)

· второй соответствует: 0,5 =< R² < 0,7 (УГ = 2/3)

· третий соответствует: 0 < R² < 0,5 (УГ = 1/3)

УГ – коэффициент уровня группы.

5.Определить количество переменных в каждой из групп.
Количество переменных в конечной модели не должно превышать значения N: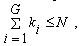

где К– общее количество переменных во всех группах; 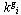– первоначальное количество переменных в группе i.

6. По критерию значимости выбрать переменные.

1. Критерий значимости для переменных выберем, как: вероятность принятия значения переменной ноля должна быть меньше 10%.

2. Критерием включения переменной в группу, участвующую в итоговой многофакторной модели, определим как, значимость переменной хотя бы в 2-х из построенных многофакторных моделей (исследуемого актива и аналогов). Если же количество переменных удовлетворяющих Критерию 2) не совпадает с определенным количеством переменных в пункте 5, то используется Критерий 3):

3. Включается та переменная, у которой Сумма вероятностей, принятия переменной ноля по исследуемой компании и аналогам, наименьшая.

7.Построение многофакторной модели, используя сформированные группы.

Для удобства практического применения модели, возможно, произвести упрощение построенной модели, используя меньшее количество входящих переменных, используя только значимые переменные.