Вопрос 3. Расчеты при начислении сложных процентов
В среднесрочных и долгосрочных финансово-кредитных операциях, если проценты не выплачиваются сразу после их начисления, а присоединяются к сумме долга, для наращивания применяются сложные проценты. В соответствии с этим процесс роста первоначальной суммы происходит с ускорением. Ускорение вызвано тем, что на каждом этапе во времени начисленные проценты присоединяются к сумме, которая служила базой для их определения. Такой процесс получил название капитализация процентов.
Наращивание по сложным процентам можно рассматривать как последовательное реинвестирование средств, вложенных под простые проценты на один период начисления.
Предположим, что проценты капитализируются один раз в год (годовые проценты) на протяжении n лет. В конце первого периода проценты равны величине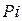 
, а наращенная сумма будет равна:
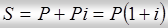
К концу второго года она достигнет величины:
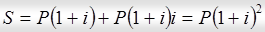и т. д.
В конце n – года наращенная сумма по сложным процентам станет равной:
.
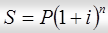Проценты за этот период будут увеличиваться с каждым годом и составят:
.
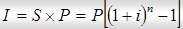Величина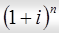 
называется множителем наращивания сложных процентов. Значения данного множителя для целых чисел n приводятся в таблицах сложных процентов для n, равных от 1 до 50, 60, 70, 80, 90, 100 лет. В случае если n > 50 и является целым числом, то искомую величину находят как произведение табличных значений для 
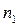и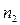 
.
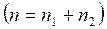В том случае, если n не является целым числом, применяется наращивание по смешанным процентным ставкам, которое определяется по следующей формуле:
,
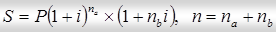где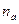 
- целое число дат;
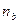- дробная часть года.
Сопоставляя формулы наращивания по простым и сложным процентам, можно сделать следующие выводы:
- Если n < 1, то
> 
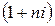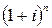- сложные проценты меньше простых; - Если n = 1, то 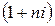= 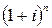- сложные проценты равны простым;
- Если n > 1, то 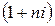< 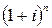- сложные проценты больше простых.
При расчете настоящей стоимости денежных средств в процессе дисконтирования по сложным процентам (Р) используется следующая формула:
Pc = S / (1 + i)n.
С учетом этих коэффициентов разработаны специальные таблицы, с помощью которых при заданных размерах ставки процента и количестве платежных периодов можно легко вычислить настоящую или будущую стоимость денежных средств.
При оценке стоимости денег во времени необходимо иметь в виду, что на результат оценки большое влияние оказывает не только размер процентов, но и периодичность выплат (или количество платежных периодов) в течение одного и того же общего срока. Иногда более выгодно инвестировать деньги под меньшую ставку процента, но с большей периодичностью выплат.