Следствия из признака эквивалентности пар

Согласно признаку эквивалентности пар, все пары, моменты которых геометрически равны, являются эквивалентными.

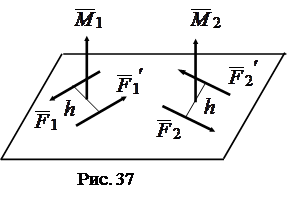Следствие 1. Не изменяя величину сил, плечо пары и направление вращения, пару можно переносить в её плоскости как жесткую фигуру (рис. 37).

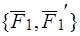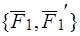Рассмотрим две пары и , лежащие в одной плоскости, причем по модулю 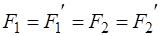, Так как плоскость пар общая и направление вращения одинаковые, то векторы 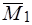и 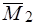параллельны и направлены в

одну сторону. Следовательно 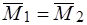, то есть моменты пар геометрически равны, пары эквивалентны: ~ .

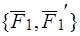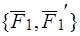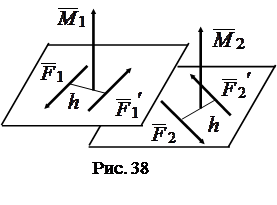Следствие 2. Не изменяя величину сил, плечо и направление вращения, пару можно переместить в параллельную плоскость (рис. 38).

Как и в предыдущем случае, моменты пар геометрически равны 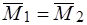. Следовательно, пары эквивалентны: ~ .

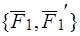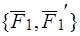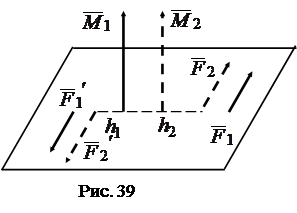Следствие 3. Пару сил можно "деформировать", то есть изменять величину сил, образующих пару и плечо пары так, чтобы произведение силы на плечо, направление вращения и плоскость пары остались неизменными (рис. 39).

Так как 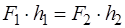, то 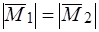. Кроме того, моменты 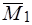и 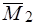параллельны и направлены в одну сторону. Тогда 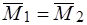, следовательно, пары эквивалентны.

Замечание. Пара, действующая на твердое тело, стремится вращать его. На первый взгляд кажется, что пара будет вращать тело вокруг середины плеча. Но, очевидно, это неверно, так как пару можно переносить в плоскости ее действия куда угодно в данном теле и, следовательно, "середина плеча" – точка совершенно неопределенная. Вопрос о том, вокруг чего поворачивается пара, относится уже к задачам динамики, так как для ответа на него нужно определить как будет двигаться тело под действием данных сил. В динамике будет показано, что всякая пара, действующая на свободное твердое тело, поворачивает это тело вокруг его центра тяжести. Если же тело имеет неподвижную ось вращения, то пара, где бы нм была расположена, будет поворачивать тело вокруг этой оси с одним и тем же вращательным усилием (моментом).

8.4. Теорема о "сложении" пар

Теорема. Всякая система, состоящая из 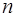пар сил, эквивалентна одной паре, момент которой равен геометрической сумме моментов пар системы.

Доказательство.

Дана система пар 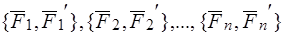, имеющих моменты .

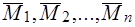Доказать, что 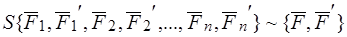и момент этой пары .

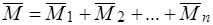Доказательство.

По основной лемме статики систему пар 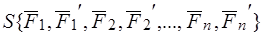приводим к двум силам 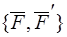. При этом главный вектор и главный момент не изменяются:

,

.

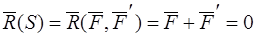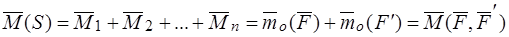Отметим, что в общем случае .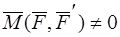

Из условия, что 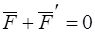, следует, что 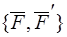- либо прямопротивоположные силы, либо пара. Но из условия, что 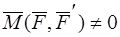, следует, что 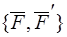не прямопротивоположные силы (так как главный момент двух прямопротивоположных сил относительно любого полюса равен нулю)

Таким образом, 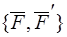есть пара, момент которой равен главному моменту исходной системы сил, то есть

.

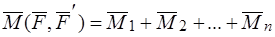Следствие. Для равновесия тела под действием системы пар необходимо и достаточно, чтобы геометрическая сумма моментов этих пар была равна нулю.