Показатель чистой текущей стоимости

Показатель чистой текущей стоимости NPV, измеряется в денежных единицах.

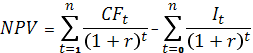
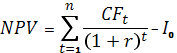
На практике встречаются варианты проектов со сроком реализации более 40 лет и постоянным темпом изменения годовой величины чистых денежных потоков. Тогда формула следующая:

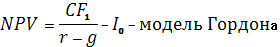
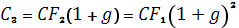
NPV представляет собой разницу между первоначальной величиной инвестиционных затрат и общей суммой дисконтированных чистых денежных потоков за все периоды времени в течение планируемого срока реализации проекта.

Правила принятия инвестиционных решений:

3) Если NPV >0 проект принимается, если < отвергается

4) Из нескольких альтернативных вариантов выбираем с максимальным NPV

4) Обладает свойством аддитивности NPV a+ NPVb = NPVa+b

Если необходимо сформировать из списка возможных капвложений портфель инвестиций, то одобрению подлежит комбинация проектов с наибольшим общим значением NPV

16 Простой срок окупаемости инвестиций (РВ). Изменяется во времени.

Существует 2 алгоритма расчета:

А. если денежные потоки поступают по годам равномерно РВ = I₀/CF

При получении дробного числа, оно округляется в сторону увеличения до ближайшего целого.

Б. если денежные потоки по годам изменяются, то срок окупаемости состоит из 2-х частей: целой j и дробной в

PB = j+d = 3+0,2= 3.2

j = (1,2+1,8+1,5)<5

(CF1+CF2+...+CFj)<=Io 1<=j<=n

d=( 5,0-(1,2+1,8+1,5))/2,5 = 0,2

d = (Io –(CF1+ CF2+...+CFj))/(CFj+1)

Правила использования РВ в инвестиционном анализе:

- проекты со РВ меньше, чем установленный инвестором (или самим предприятием) нормативный промежуток времени – принимаются, с большим – отвергаются. В качестве нормативного может выступать требование банка к возврату кредита

- из нескольких взаимоисключающих проектов, выбираем проект с меньшим значением РВ

Преимущества:

- легкость расчета

- простота для понимания

- можно ранжировать проекты

Недостатки:

- игнорируется временная ценность денежных вложений

- игнорирует денежные потоки по ту сторону РВ инвестиций, что может привести к ошибке

- РВ не обладает свойством аддитивности РВа+РВв не= РВа+в

17. Модифицированная внутренняя норма рентабельности инвестицийMIRR. Он убирает отдельные недостатки IRR, то есть в отличии от IRR рассчитанный для нетрадиционных денежных потоков имеет только одно значение. MIRR представляет собой % ставку, которая уравнивает дисконтированную стоимость денежных потоков, реинвестированный по ставке r с текущей стоимостью капвложений. Будущая оценка реинвестированных денежных потоков в научной литературе называется заключительной стоимостью (TV).

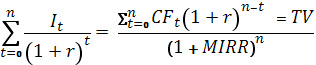
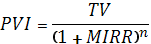
Если капвложения носят единовременный характер и происходят в начальный период инвестирования t=0, а операционные денежные потоки генерируются проектом начиная с 1-го года, то формула упрощается:

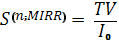
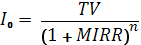
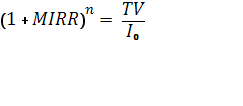
Коэффициент будущей стоимости при ставке, определяемой MIRR за n периодов времени.

Показатель внутренней нормы рентабельности инвестиций IRR – это такая процентная ставка, при которой NPV равен 0.

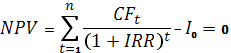
IRR представляет собой процентную ставку, которая делает текущую стоимость проектных денежных потоков равной начальным инвестициям. Следовательно IRR приравнивает проектную NPV к нулю. IRR определяет максимально приемлемую % ставку, пр которой ещё можно без потерь для собственников компании вкладывать средства в ИП.

IRR является минимальной величиной рентабельности, при которой занятые средства окупятся за планируемый срок реализации проекта. Классическое правило для использования IRR в обосновании инвестиционных решений звучит так: если IRR превосходит цену капитала, компания должна принять проект. В противном случае он должен быть отвергнут.

Существует 4 способа нахождения IRR:

1) метод проб и ошибок

2)использование финансового калькулятора или программных продуктов

3)использование упрощенной формулы

IRR = r_b+(r_a-r_b)*NPVb/(NPVa-NPVb)

- r_b<IRR<ra

- NPVa<0<NPVb

Например: определим IRR, если начальные инвестиционные затраты 20млн.руб, денежные потоки по годам – 6,8 и 14 млн.руб.

IRR=0,15+(0,2-0,15)*0,471466/( 0,471466- (-1,342594)) = 16,3%

Если требуется дальнейшее уточнение, то ставку определяют в диапазоне от 16 до 17 %.

IRR = 0,16+ (0,17-0,16)* (0,087618/(0,087618- (-0,286488))= 0,1623= 16,23%

4) применяя стандартные значения текущей стоимости аннуитета при постоянном значении чистого денежного потока. Если из года в год проект производит постоянную величину ЧДП, то процедура нахождения искомого показателя значительно упрощается:

Io/CF = a(n;IRR), где а – коэффициент текущей стоимости обычного аннуитета

Зная величину срока реализации проекта n, в таблицах 6-ти функций для стандартного значения текущей стоимости аннуитета можно определить искомое значение r, которое и будет выбрано в качестве IRR

Преимущества IRR:

- Легок для понимания

- Учитывает временную ценность денежных вложений

- Показывает рисковый край (предельное значение % ставки)

Недостатки:

- нетрадиционные денежные потоки способствуют возникновению множественности значений IRR . Есть денежные потоки традиционные (прямые -+++++ и обратные +-------) а есть нетрадиционные (-++-+++).