Структура процентных ставок

Доходность любого актива, который находится в обороте на рынке, прежде всего, отражает его степень риска и общее состояние рынка. На эффективно действующих рынках более рискованные активы обеспечивают, как правило, более высокую доходность. Если финансовый рынок находится в стадии формирования, он не всегда гарантирует установление таких рыночных цен на активы, которые отвечали бы их степени риска. В таких случаях на рынке могут быть в обороте активы одного уровня доходности, но разной степени риска.

При этом на любом финансовом рынке находятся в обращении активы, которые обеспечивают инвесторам минимальный доход и при этом считаются безрисковыми. Это краткосрочные государственные долговые обязательства: казначейские векселя, облигации внутреннего государственного займа и др. Они обеспечивают довольно невысокий по сравнению с другими инвестициями уровень дохода, но являются высоколиквидными активами, которые гарантируют получение дохода на уровне и в сроки, предусмотренные условиями выпуска, то есть государственные ценные бумаги являются практически безрисковыми, высоконадежными активами. Реальная доходность краткосрочных ценных бумаг находится на уровне 2-4%. Средне- и долгосрочные государственные бумаги считаются более рискованными и характеризуются преимущественно высоким уровнем доходности.

Номинальный доход может быть разным в зависимости от инфляционных ожиданий в государстве. Там, где инфляция составляет 2-4% в год, доходность государственных ценных бумаг находится на уровне 5-7%. При высоких уровнях инфляции доходность государственных ценных бумаг может достигать десятков процентов. Например, доходность облигаций внутреннего государственного займа Украины в 1995 г. составляла 90%.

Поскольку при расчете процентных ставок по государственным ценным бумагам используются ожидаемые или прогнозируемые уровни инфляции, на время выплаты процентов такие бумаги могут иметь реальную доходность, которая равняется нулю, или приносить убытки. Схематично зависимость уровня дохода по разным финансовым активам от степени их риска показана на рис. 1. Кривая 1 отражает доходность финансовых активов, которые находятся в обороте на финансовых рынках, которые находятся в стадии формирования, а кривая 2 – на развитых финансовых рынках.

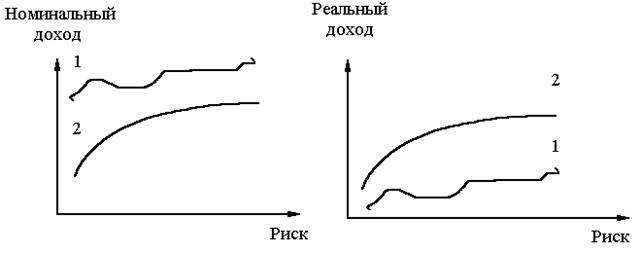
Рис. 1. Зависимость уровня дохода по финансовым активам от степени их риска

На развитых финансовых рынках существуют эффективные механизмы установления доходности актива на уровне, который отвечает степени его риска. Именно доходность любого финансового актива определяется доходностью безрискового актива и премией за риски, характерные для такого актива.

Другими словами, любая процентная ставка k на рынке является суммой безрисковой, или безопасной, процентной ставки k_б и премии за риск k_р:

k = k_б + k_р. (8)

Безрисковая процентная ставка – это номинальная процентная ставка по краткосрочным государственным ценным бумагам, которая является, в свою очередь, суммой двух составных – реальной процентной ставки k₀ и поправки на инфляцию k_i:

k_б= k₀ + k_i.

Составная k_i рассчитывается на основе прогнозируемых уровней инфляции и потому в случае нестабильной экономической и политической ситуации в стране может существенно отличаться от реальных темпов инфляции. Например, в начале года были эмитированные 12-месячные государственные облигации с купонными выплатами на уровне: k_б= k₀ + k_i = 24%, где k₀ = 4% – запланированная реальная доходность облигаций и k_i = 20% – прогнозируемый уровень инфляции на год. Если реальный уровень инфляции за год составлял 27%, купонные выплаты в конце года в объеме 24% не только не принесут дохода собственнику облигаций, а и не сохранят инвестированные средства от инфляции.

Этот пример свидетельствует о том, что в условиях нестабильной экономической ситуации и неразвитого финансового рынка государственные облигации не могут играть такую роль, как на развитых финансовых рынках. Так, на развитых рынках, где уровни инфляции невысокие и более прогнозируемые, краткосрочные государственные ценные бумаги являются высоконадежными, высоколиквидными активами, уровень дохода по которым служит основой для формирования рыночных процентных ставок.

В Украине, где финансовый рынок находится в стадии развития, основой для формирования рыночных процентных ставок, ориентиром цены на деньги выступают ставки рефинансирования и учетная ставка Национального банка Украины.

Ставка рефинансирования – это выраженная в процентах плата за кредиты, которые предоставляются коммерческим банкам.

Учетная ставка НБУ, которая является наиболее низкой среди ставок рефинансирования, – это выраженная в процентах плата, которую берет Национальный банк Украины за рефинансирование коммерческих банков путем покупки векселей до наступления срока платежа по ним и удерживает с номинальной суммы векселя.

Составная процентной ставки k_p отражает риск инвестирования в конкретный финансовый актив и является суммой трех составных

k_р = k_л + k_п + k_ч, (9)

где k_л – премия за риск ликвидности;

k_п – премия за риск неплатежа;

k_ч – премия за риск, связанный со сроком оборота данного финансового актива.

Рассмотрим подробнее эти составные. Все они отражают степень неуверенности в получении дохода по финансовому активу, а именно степень неуверенности в получении дохода от владения данным финансовым активом и дохода от продажи его на рынке. Премия за риск ликвидности k_л отражает риск неполучения дохода от продажи финансового актива и является платой за то, что данный актив нельзя будет быстро и без потерь продать на рынке, то есть быстро и без потерь превратить на денежную наличность. Чем более ликвидным является актив, тем меньше премия за риск ликвидности в общей величине процентной ставки.

В пределах одного финансового рынка более ликвидными являются государственные ценные бумаги и облигации и акции известных корпораций. Такие бумаги находятся в обороте, как правило, на биржах и во внебиржевых торговых системах высокого уровня. Ценные бумаги новых компаний, которые попадают в руки инвесторов вследствие частного размещения, являются рискованными как с точки зрения их ликвидности, так и с точки зрения своевременного получения дохода запланированного уровня.

Доход от владения активом состоит из регулярных периодических процентных или дивидендных выплат и суммы, полученной при его погашении. Чем больше степень неуверенности в получении данных выплат по активу, тем большей будет премия k_п за риск неплатежа. Риск неплатежа отражает риски несвоевременной уплаты дохода (процентов или основной суммы долга), уплаты дохода не в полном объеме или полной его неуплаты. С этой точки зрения привилегированные акции являются более рискованными, чем облигации, а простые акции – более рискованными, чем привилегированные. Собственники облигаций являются кредиторами предприятия-эмитента. Обязательства по облигациям относительно выплаты процентов и суммы основного долга выполняются эмитентом в первую очередь. После этого удовлетворяются требования держателей привилегированных акций, а потом держателей простых акций. Чем больше риск неуплаты по финансовому активу, тем большей будет соответствующая премия за риск, а, следовательно, общая доходность актива.

Премия за риск, связанный со сроком оборота финансового актива, как правило, увеличивается с его увеличением. Больший период времени связан с большей неопределенностью, а, следовательно, с большим риском, поэтому спрогнозировать будущую ситуацию на рынке или будущие процентные ставки тем сложнее, чем больше срок прогноза.

Номинальные процентные ставки и номинальная доходность долгосрочных обязательств часто не отвечают будущим рыночным процентным ставкам. Реальная доходность долговых обязательств, как правило, отвечает рыночной. Так, доходность долгового обязательства с плавающей ставкой всегда отвечает рыночной, поскольку изменяется в соответствие с рыночной конъюнктурой. Доходность актива с фиксированным доходом отвечает рыночной лишь при продаже его на рынке, поскольку корригируется изменением его рыночной стоимости. Владение активом с фиксированным доходом обеспечивает доходность выше рыночной при падении процентных ставок на рынке и ниже рыночной при возрастании процентных ставок.

С увеличением срока оборота финансового актива возрастает и неопределенность, связанная с ликвидностью этого актива и своевременным получением дохода по нему. Поэтому можно считать, что величина k_ч – это премия за риски, связанные с будущим изменением процентных ставок на рынке, с изменениями в ликвидности и в уверенности получения дохода по такому финансовому активу.

Зависимость между доходом при погашении и сроком погашения долгового обязательства показана на рис. 2. Кривая 1 графически изображает нормальную зависимость между сроком погашения обязательства и его доходностью. Чем больше срок оборота долгового обязательства, тем большей является ставка дохода по нему, что отвечает стабильной ситуации на финансовом рынке. Кривая 2 отражает обратную зависимость между доходностью и сроком оборота актива, при которой краткосрочные финансовые активы имеют доходность выше, чем долгосрочные. Такая зависимость может наблюдаться в периоды кризисных явлений в экономике. Горизонтальная прямая 3 означает независимость процентных ставок от сроков погашения долговых обязательств и случается довольно редко в периоды неопределенности в экономике.

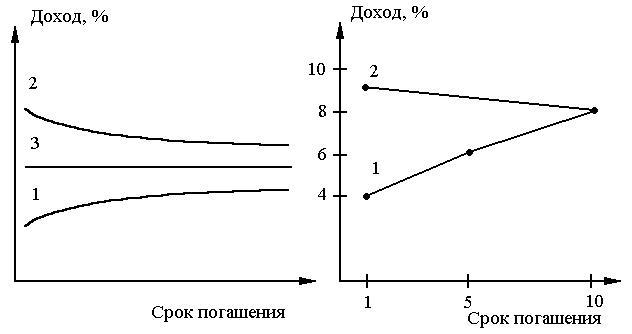
Рис. 2. Зависимость между доходами при погашении и сроком погашения долгового обязательства

Рис. 3. Структура процентных ставок по долговым обязательствам на рынке США и Германии

В последнее время в некоторых странах с высокоразвитой экономикой наблюдается тенденция к горизонтальной прямой 3.

Структуру процентных ставок по долговым обязательствам на рынке США (1) и Германии (2) в 1992 г. представлено на рис. 3. Рынок США характеризуется нормальной зависимостью, а Германии – обратной.

Зависимость процентных ставок по инструментам долга, которые находятся в обороте на рынке США, от степени риска долговых обязательств приведена на рис. 4.

Существует зависимость между ожиданиями рынка относительно изменений процентных ставок в будущем и текущей формой кривой доходности. Так, нормальная зависимость между доходностью и сроком погашения финансового актива может свидетельствовать о повышающих тенденциях относительно рыночных процентных ставок. Сделав предположения о том, что коротко- и долгосрочные инвестиции должны обеспечивать инвестору одинаковый уровень дохода, можно оценить будущие изменения в рыночных процентных ставках.

Рис. 4. Зависимость процентных ставок по инструментам долга от степени их риска

Предположим, что инвестор имеет возможность реализовать одну из двух стратегий: инвестировать сумму С₀ на n лет под ставку k_n, или вложить ту сумму на n–1 лет под процентную ставку k_n–1, а после этого полученную сумму инвестировать еще на один год. При первой стратегии наращенная сумма С_н может быть определена по формуле

С_н = С₀ (1 + k_n)ⁿ.

Вторая стратегия предусматривает, что наращенная сумма С_н1 будет вычислена по формуле

С_н1 = С₀ (1 + k_n–1)^n–1 (1 + k₁),

где k₁ – процентная ставка по инвестированию средств через n–1 лет на 1 год, то есть форвардная процентная ставка. Считая, что инвестор получает одинаковую сумму С_н через n лет, реализуя первую ли вторую стратегию, получим равенство:

С₀ (1 + k_n)ⁿ = С₀ (1 + k_n–1)^n–1 (1 + k₁),

откуда

k₁ = (1 + k_n)ⁿ : (1 + k_n–1)^n–1 – 1. (10)

Если имеет место нормальная кривая доходности (k_n > k_n–1), форвардная одногодичная процентная ставка k₁ будет больше текущей одногодичной процентной ставки. Причем чем большей будет разность между коротко- и долгосрочными текущими процентными ставками, тем большее возрастание процентных ставок ожидает рынок.

Пример. Инвестор имеет возможность вложить средства в двухлетнюю дисконтную облигацию, которая обеспечивает доходность 10% и будет погашена по номиналу 1 000 ден. ед. или инвестировать средства в одногодичную облигацию с уровнем дохода 9% и номиналом 1 000 ден. ед., а через год реинвестировать средства в такую точно облигацию. Какую доходность должна иметь одногодичная облигация через 1 год, чтобы результат от инвестирования средств в первом и втором случае был одинаковый?

Рыночная стоимость двухлетней облигации, которая обеспечит доход на уровне 10%, Р₀ = 1 000 : (1 + 0,1)² = 826,45 ден. ед.. Инвестировав 826,45 ден. ед. в одногодичную облигацию с доходом 9%, через год инвестор получит сумму: С_н = 826,45 (1 + 0,09) = 900,83 ден. ед.. Для того чтобы, реинвестировав средства в такую точно облигацию, получить в конце второго года 1 000 ден. ед., необходимо, чтобы доходность одногодичной облигации k₁ выросла до 11%:

1 000 = 900,83 (1 + k₁), откуда k₁ = 0,11, или 11%.

Аналогичный результат можно получить, использовав формулу (1.10):

k₁ = (1 + 0,1)² : (1 + 0,09) – 1 = 0,11.

Итак, при инвестировании 826,45 ден. ед. в облигации можно получить доход в размере 1 000 ден. ед., если инвестировать средства в двухлетнюю облигацию со ставкой дохода 10% или в одногодичную облигацию со ставкой дохода 9% со следующим реинвестированием средств в такую точно облигацию с уровнем дохода 11%.

При инвестировании средств в двухлетнюю облигацию с уровнем дохода 10% и одногодичную облигацию с уровнем дохода 9% можно получить одинаковый доход, если доходность одногодичной облигации возрастет до 11%.

При расчете доходности отдельных финансовых активов или портфеля активов используют разные типы процентных ставок: среднеарифметические, среднегеометрические или внутренние. Среднеарифметическая процентная ставка вычисляется по формуле

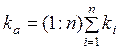, (11)

где k_і – доходность актива за і-й период;

n – количество периодов.

Эта ставка определяет среднюю доходность актива на протяжении n периодов при условии, что доход, полученный на протяжении любого из n периодов, не реинвестируется, а изымается из оборота.

Среднегеометрическая процентная ставка определяется из условия реинвестирования в следующем периоде дохода, полученного на протяжении предшествующего периода:

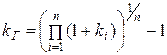. (12)

Внутренняя процентная ставка определяется с учетом временного фактора в оценке дохода по активу или портфелю активов:

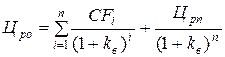, (13)

где Ц_ро – рыночная цена актива (или портфеля активов) в начальный момент времени;

Ц_рп – рыночная цена портфеля на конец n-го периода;

CF_i – денежный поток (доход по активу) за i-й период.

При определении доходности финансового актива Ц_рп означает возможную цену продажи актива на рынке или сумму получения при погашении финансового актива. Для того чтобы определить в каждом конкретном случае внутреннюю процентную ставку, нужно решить уравнение (1.13) относительно k_в.

Пример. Предположим, что –5%, 15% ,11% – доходности портфеля за 1-й, 2-й, 3-й периоды соответственно. Тогда средняя арифметическая процентная ставка равняется: (–5 + 15 + 11) : 3 = 7%. При этом предполагается, что в конце 1-го периода дополнительно инвестируются 5% средств, а в конце 2-го и 3-го периодов изымаются соответственно 15 и 11% средств.

Среднегеометрическая ставка равняется:

[(1 – 0,05)(1 + 0,15)(1 + 0,11)]^1/3 – 1 = 0,067, или 6,7%.

При анализе структуры процентной ставки основное внимание было сосредоточенно лишь на виды рисков, присущих финансовым активам. Эти риски являются прямым следствием рисков, связанных с деятельностью эмитентов данных активов, а именно предпринимательских рисков. Понимание сути и методов оценивание предпринимательских рисков дает возможность лучшее понять принципы деятельности субъектов финансового рынка: финансовых институтов и корпораций, а также сущность и тенденции развития рынков разнообразных финансовых активов.