Средние и относительные величины в АХД

Экономические явления, изучаемые в АХД, имеют количественную определённость, которая выражается в абсолютных и относительных величинах. Абсолютные величины характеризуют явление количественно, независимо от остальных аналогичных явлений. Распространённым приёмом анализа является расчёт средних величин абсолютных показателей.

Роль средних величин заключается в обобщении, т.е. замене множества индивидуальных значений признака некоторой средней величиной, характеризующей всю совокупность явлений. Средняя величина обобщает качественно однородные значения признака и не является фиксированной. Средняя арифметическая величина – это такое среднее значение признака, при вычислении которого общий объём признака в совокупности равномерно распределяется между всеми её единицами:

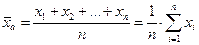(3.1).

Средняя геометрическая используется в анализе для расчёта средних темпов роста объёмов производства, инфляции и т.п. Показатель рассчитывается по формуле:

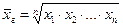(3.2).

Классификация показателей подразумевает их деление на интервальные и моментные. Для усреднения интервальных показателей (выручка, прибыль) используется средняя арифметическая. Для усреднения моментных показателей (стоимость основных средств, численность персонала) применяется формула средней хронологической:

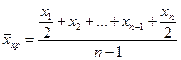(3.3).

Относительные показатели отражают соотношение величины изучаемого явления с величиной какого-либо другого явления или с величиной этого же явления по другому объекту. Относительные показатели получаются в результате деления одной величины на вторую. При этом они могут выражаться в форме коэффициентов, процентов или индексов. Индекс – это относительная величина, характеризующая соотношение двух значений показателя, описывающего одно и то же явление:

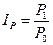(3.4), где

P₁ – сравниваемый уровень показателя; P₀ – базисный уровень показателя.

Индекс называется простым, если исследуемый признак берётся без учёта его связи с другими признаками, и сводным, если исследуемый признак берётся по логически связанным элементам. Сводный индекс даёт характеристику изменения оцениваемого показателя в среднем. При этом сводный индекс чаще всего бывает агрегатным. Агрегатный индекс всегда состоит из двух компонент: индексируемого признака P, динамика которого исследуется, и весового признака Q.

С помощью индексного метода в АХД решаются следующие задачи:

- оценка изменения уровня явления, выявление роли отдельных факторов в изменении результативного показателя;

- оценка влияния изменения структуры совокупности на динамику среднего уровня анализируемого показателя;

- пересчёт показателей для сравнения и т.п.