Задания для самоконтроля по теме «Составление графиков возврата долгосрочных кредитов» (погашение периодическими взносами)
1. Предприятие получает кредит в сумме 150000 руб. сроком на 6 лет. Платежи в счет погашения кредита вносятся ежегодно в сумме 15000 руб. плюс процент 70%. В конце 6 летнего периода уже осуществлены пять платежей по 15000 руб. (75000 руб.) и остается невыплаченной сумма в 75000 руб., которую полностью выплачивают по окончании срока кредита. Проиллюстрируйте такой порядок погашения в таблице и сделайте таблицу обслуживания долга при погашении кредита равными порциями – 25000 руб.
«Амортизационное» погашение кредита.
При "амортизационном" погашении основную сумму кредита выплачивают постепенно на протяжении срока кредита. Платежи осуществляют равными суммами регулярно (как правило, ежемесячно, ежеквартально или раз в полгода), и они включают определенную часть суммы кредита и процент. Вместе с последним взносом сумму кредита погашают. Этот принцип используют при ипотечном кредите. Многие западные кредитные инвесторы используют эту схему в качестве базового графика возврата долга предприятием-заемщиком.
Задача 3.5.Кредитный инвестор предлагает предприятию кредит под 12 процентов годовых срок на 4 года при полугодовой схеме возврата долга. Предприятие планирует привлечь 800000 рублей. Необходимо рассчитать график обслуживания долга.
Прежде всего, необходимо вычислить величины полугодовой выплаты. При расчете этой суммы используется концепция стоимости денег во времени. Применительно к данному вопросу она заключается в том, что приведенная к настоящему моменту сумма всех платежей должна быть равной сумме кредита.
Если PMT - неизвестная величина годовой выплаты, а S - величина кредита, то при процентной ставке кредита і и количестве периодических платежей n величина PMT может быть вычислена с помощью уравнения:
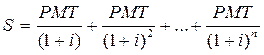
Решение этого уравнения можно произвести с помощью финансовых таблиц или электронного процессора EXCEL. Для данного примера сумма годового платежа равна 128829 руб.. Таблица обслуживания долга имеет вид:
| Год | Начальный баланс долга (руб.) | Погашение долга (руб.) | Проценты (руб.) | Годовая выплата (руб.) | Конечный баланс долга (руб.) |
| 3 = 5-4 |  4 = (столб. 2×0,12) / 2 (полугодовая выплата) | 6 = 2 ой год из столб. 2 | |||
| Итог |
Для сравнения приведем график обслуживания той же суммы кредита по схеме погашения основной части долга равными порциями:
| Год | Начальный баланс долга (руб.) | Погашение долга (руб.) | Проценты (руб.) | Годовая выплата (руб.) | Конечный баланс долга (руб.) |
| 3 = 5-4 | 4 = (столб. 2×0,12) / 2 (полугодовая выплата) | 6 = 2 ой год из столб. 2 | |||
| - | |||||
| Итог |
Поскольку суммарные процентные выплаты во второй схеме существенно меньше, может показаться, что этот график более выгоден. На самом деле обе схеме одинаковы в смысле “справедливости” взаимоотношений между кредитором и заемщиком, так как современное дисконтированное значение всех годовых платежей во второй схеме, как и первой, равно исходной сумме кредита 800000 руб. (столб 3).